Урок по математике на тему Сложение чисел с разными знаками

Предмет - математика

Класс - 6

Тема урока: «Сложение чисел с разными знаками».

Тип урока: урок изучения нового материала

Цели урока:

Образовательные: изучить правила сложения чисел с разными знаками:

1. на координатной прямой

2. используя алгоритм сложения

и совершенствовать вычислительные навыки.

Развивающие: развивать умения наблюдать, сравнивать, анализировать, строить гипотезы и делать выводы, расширять математический и общий кругозор, совершенствовать графическую культуру и устную математическую речь.

Воспитательные: формировать такие качества личности, как трудолюбие, внимательность, активность, умение слушать мнения других.

Оборудование: компьютер, экран, проектор, раздаточный материал для самостоятельной работы на 2 варианта, блок-схема алгоритма сложения рациональных чисел.

Ход урока

1.Организационный этап:

-приветствие;

-готовность учащихся к уроку;

-состояние рабочего места учащихся: наличие тетрадей, учебников, чертежных принадлежностей;

-отсутствующие на уроке (сообщают дежурные)

Учитель. Запишите в тетрадях число и тему урока: «Сложение чисел с разными знаками».

2. Подготовка к изучению нового материала. Актуализация знаний.

Вопросы для повторения (на экране/доске):

1. Какие числа называются рациональными? (отрицательные числа, ноль и положительные числа)

2. Расположение рациональных чисел на координатной прямой (отрицательные - левее нуля, положительные - правее нуля, большее число расположено правее)

3. Сложение и вычитание чисел на координатной прямой (при вычитании - перемещение влево, при прибавлении - перемещение вправо)

4. Законы сложения (переместительный закон a+b=b+a и сочетательный закон (a+b)+c=a+(b+c))

5. Правила знаков при раскрытии скобок (если перед скобками знак минус, то знаки в скобках меняют, если перед скобками знак плюс, то знаки в скобках сохраняют)

6. Определение модуля числа ()

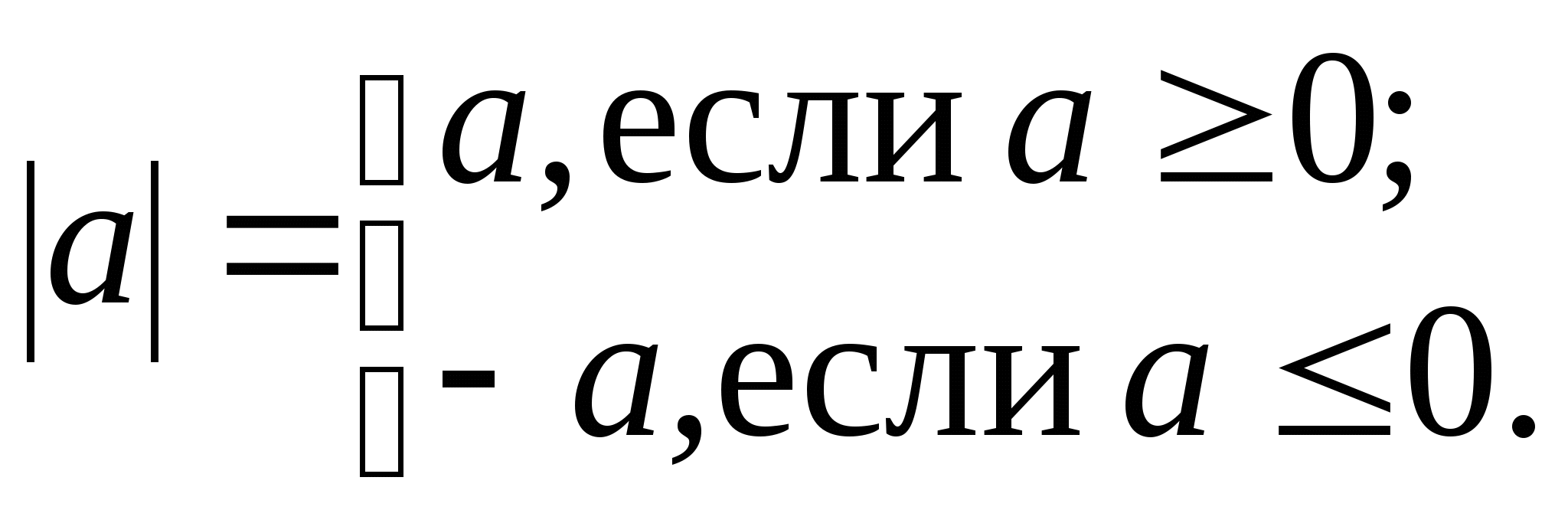Задача №1.

Записать решение в тетради. Решение с комментированием.

Построй математическую модель, описывающую данные изменения, и запиши результат с помощью положительных и отрицательных чисел:

• доход 5 руб. и расход 8 руб. (+5+(8));

• расход 30 руб. и расход 40 руб. (30+40);

• расход 2 тыс. руб. и доход 7 тыс. руб. (2+7);

• уменьшение температуры на 6 °С и увеличение на 2 °С (6+2);

• уменьшение температуры на 3 °С и уменьшение на 9 °С (3+(9));

• увеличение уровня воды в реке на 25 мм и уменьшение на 40 мм (+25+(40));

• из автобуса вышли 7 человек, а вошли 6 человек (7+6);

• со склада увезли 4 т картофеля, а привезли 10 т (4+10).

Задача №2. (Устно)

Придумай ситуацию, математической моделью которой может служить данное выражение:

а) (9) + (+4); б) (+6) + (+3); в) (5) + (2); г) (1) + (+7).

3. Изучение нового материала.

Задача №3.

У доски решают 2 учащихся, остальные - в тетрадях.

Выполни сложение чисел с помощью координатной прямой:

а)( 3) + (+8); б)( 1) + (4); в) (6)+ (+4); г) (2) + (+5) + (3).

( 1) + (4) = 5 (6)+ (+4) = 2

Задача №4.

Найди результат действия, ориентируясь на некоторую практическую ситуацию, и проверь полученный ответ с помощью координатной прямой. Что общего в примерах каждого столбика? Сделай вывод.

а)(+2) + (+3) б)(-3) + (+4) в) (+2)+ (-5) г) (-4)+ (+4)

(-5) + (-1) (-1) + (+5) (+1) + (-3) (+1) + (-1)

(-3) + (-4) (+4)+ (-2) (-4) + (+3) (-5)+ (+5)

(-2) + (-7) (+6) + (-3) (-6) + (+1) (+2)+ (-2)

а) сложение чисел с одинаковыми знаками; знаки суммы и слагаемых совпадают

б) сложение чисел с разными знаками; сумма больше нуля

в) сложение чисел с разными знаками; сумма меньше нуля

г) сложение противоположных чисел; сумма равна нулю

Учитель. Но выполнение сложения чисел на координатной прямой не всегда удобно, поэтому надо иметь алгоритм, который позволит складывать рациональные числа без координатной прямой.

Рассмотри блок- схему алгоритма сложения рациональных чисел. Верно ли она составлена?

Задача №5.

Работа по цепочке с устным проговариванием решения по блок-схеме.

Пользуясь алгоритмом сложения рациональных чисел, найди сумму:

а)(-28) + (-14) б)(-32) + (+32) в)(-9) + (+17) г)(+3) + (-18)

(-2,4) + (-3,6) (-1,18) + (+1,18) (-0,8) + (+4) (+1,7) + (-7,3)

Задача №6. (Устно)

Определи знак суммы:

а) (-12) + (-7); в) (+15) + (-8); д) (-24) + (+19); ж) (+3,7) + (-8,4);

б)(-8) + (+3); г) (-6)+ (-11); е) (+53) + (-35); з) (-245) + (+300).

Ответы: а) -; б) -; в) +; г) -; д) -; е) +; ж) -; з) +.

Задача №7.

1) Сформулируй переместительное свойство сложения рациональных чисел и запиши его на математическом языке. Проверь переместительное свой­ство для значений переменных: а) -4,8 и 0,3; б) - и -1,15.

2) Сформулируй сочетательное свойство сложения рациональных чисел и запиши его на математическом языке. Проверь сочетательное свойство для значений переменных: а)-1,5; +2,7 и -0,2; б) -; -1,4 и +0,8.

а) (-1,5 +2,7) -0,2 = -1,5 +(2,7-0,2) 1=1

б) (-+ (-1,4)) +0,8 = -+ (-1,4 +0,8) -3,2=-3,2

Задача №8.

Работа в парах.

Раскрой скобки и запиши выражение в виде алгебраической суммы. Есть ли в этой сумме противоположные слагаемые? Если да, подчеркни их.

1. (-3) + (-8) + (+9) + (-6) + (+8); 3) (-а) + (+b) + (-х) + (-b) + (-x);

2) (+0,2) + (-1,4) + (-2,3) + (-1,4); 4) (+n) + (-d) + (-у) + (-n) + (-d).

Ответы:

1. -3 - 8 + 9 - 6 + 8; 3) -а + b - х - b - x;

2) 0,2 - 1,4 - 2,3 - 1,4; 4) n - d - у - n - d.

Задача №9.

Один учащийся у доски на слух записывает получающиеся равенства, а остальные учащиеся выполняют проверку своих решений по этой записи.

Переведи с русского языка на математический:

1. Сумма противоположных чисел равна нулю (-а+а=0).

2. Модули противоположных чисел равны (|а|=|-а|).

3. Сумма любого числа с нулем равна самому числу (а+0=а).

4. При перестановке слагаемых значение суммы не меняется (а+b=b+a).

5)Чтобы к сумме двух чисел прибавить третье число, можно к первому

числу прибавить сумму второго и третьего ( (a+b)+c=a+(b+c) ).

Задача №10.

Решение выполняется по цепочке у доски.

Сложив сначала противоположные числа, найди значения выражений:

а) 158 - 392 + 75 - 158 - 75; в) -2,49 + 3,5 + 2,49 - 1,67 - 3,5;

б) ; г) .

Ответы: а) -392; б); в) -1,67; г) 0.

Самостоятельная работа

Выполняется с использованием раздаточного материала на отдельных листах и через 3 минуты сдается учителю. Ответы сверяются с эталоном.

Вычисли наиболее удобным способом:

1 вариант

2 вариант

4. Подведение итогов урока.

1. Учащиеся рассказывают о том, что они делали на уроке:

- выполняли сложение чисел с разными знаками с помощью координатной прямой;

- узнали, что такое алгебраическая сумма чисел;

- знакомились с блок-схемой алгоритма сложения рациональных чисел;

- рассматривали применение алгоритма сложения чисел с разными знаками;

- использовали приемы рациональных вычислений (переместительный и сочетательный законы).

2. Выставление отметок за работу на уроке.

5. Домашнее задание (на экране)

1. Глава 3 §2 п.1

2. Пользуясь алгоритмом сложения рациональных чисел, найди сумму:

а) (-36)+ (-9) б) (-5,8) +0 в) (-8)+ (+11) г) (-21) +(+16)

(-0,7)+ (-0,5) 0+ (-4,3) (-1,6)+ (+3) (-5,2)+ (+4,7)

3. Вычисли и расположи ответы примеров в порядке возрастания. Что обозна­чает получившееся слово? Что тебе известно о нем?/Килиманджаро/

4. Реши уравнения и неравенства:

а) | х |=7; б) | у |=1,2; в) | х | < 4; г) | у | < 5.

6. Резервное задание.

Математические софизмы.

Софизм (от греческого sophisma  хитрая уловка, измышление)  логически неправильное рассуж­дение, выдаваемое за правильное.

Дважды два  пять!

Возьмем верное равенство: 28 + 8  36 = 35 + 10  45.

В каждой части этого равенства вынесем за скобки общий множитель:

4(7 +29) = 5(7 +29).

Теперь, разделив обе части равенства на общий множитель (7 + 2  9), полу­чим, что 4 = 5, то есть 2 • 2= 5. Где ошибка?

/Выполнено деление на ноль/

Дополнительная литература:

Лебединцева Е.А., Беленкова Е.Ю. Математика 6 класс. Задания для обучения и развития учащихся. - М.:Интеллект-центр, 2005.