- Учителю
- Урок - семинар на тему «Решение уравнения sin x + cos x = 1»
Урок - семинар на тему «Решение уравнения sin x + cos x = 1»
Муниципальное бюджетное образовательное учреждение
средняя образовательная школа №1
имени генерал - лейтенанта Б.П. Юркова
г.Зверева Ростовской области.
Урок - семинар на тему
«Решение уравнения sin x + cos x = 1»
учитель математики МБОУ СОШ №1
им. Б.П. Юркова
Куц Фёдор Иванович
г. Зверево
2015 г.
Перед человеком к разуму три пути: путь размышления - это самый благородный; путь подражания - это самый легкий; путь личного опыта - самый тяжелый путь.
Конфуций
Цели урока:
Главная дидактическая цель: рассмотреть все возможные способы решения данного уравнения.
Обучающие: изучение новых приемов решения тригонометрических уравнений на примере данного в творческой ситуации урока-семинара.
Развивающие: формирование общих приемов решения тригонометрических уравнений; совершенствование мыслительных операций учащихся; развитие умений и навыков устной монологической математической речи при изложении решения тригонометрического уравнения.
Воспитывающие: развивать самостоятельность и творчество; способствовать выработке у школьников желания и потребности обобщения изучаемых фактов.
Вопросы для подготовки и дальнейшего обсуждения на семинаре.
1) Введение вспомогательного угла.
2) Использование универсальной тригонометрической подстановки:
3) Сведение к однородному уравнению.
4) Применением формул сложения тригонометрических функций
5) Возведение обеих частей уравнения в квадрат.
6) Применение формул двойного и половинного аргумента.
7) Применение основного тригонометрического тождества.
8) Приведение к квадратному уравнению относительно одной из функций.
9)Графическое решение уравнения.
Все учащиеся разбиваются на группы (по 2-3 человека) в зависимости их индивидуальных способностей и желания. Каждой группе определяется задание для подготовки и выступления на уроке-семинаре. Выступает один человек от группы, а остальные учащиеся принимают участие в дополнениях и исправлениях ошибок, если в этом возникнет необходимость.
Организационный момент.
Учащимся сообщаются:
Тема урока: «Различные способы решения тригонометрического уравнения sin x + cos x = 1».
Форма проведения: урок - семинар.
Задачи урока:
а) рассмотреть возможность решения одного и того же уравнения различными способами;
б) познакомиться с различными общими приемами решения тригонометрических уравнений;
в) изучение нового материала (введение вспомогательного угла, универсальная подстановка).
План семинара:
1) Введение вспомогательного угла.
2) Использование универсальной тригонометрической подстановки:
3) Сведение к однородному уравнению.
4) Применением формул сложения тригонометрических функций
5) Возведение обеих частей уравнения в квадрат.
6) Применение формул двойного и половинного аргумента.
7) Применение основного тригонометрического тождества.
8) Приведение к квадратному уравнению относительно одной из функций.
9)Графическое решение уравнения.
-
Решение первой группы.
Решение уравнения sin x + cos x = 1 методом «Введения вспомогательного угла».
Если дано уравнение a sin x + b cos x = с, то разделив обе части уравнения на выражение
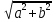 и вводя дополнительный угол
и вводя дополнительный угол 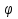 , получим уравнение cos
, получим уравнение cos 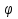 sin x + sin
sin x + sin 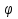 cos x =
cos x = 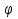 .
.
Откуда sin (x + 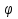 ) =
) = 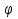 .
.
(Или sin 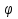 sin x + cos
sin x + cos 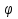 cos x =
cos x = 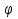 . Откуда cos (x +
. Откуда cos (x + 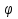 ) =
) = 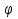 ).
).
Для уравнения sin x + cos x = 1 имеем: a = 1, b = 1: 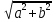 =
= 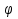 =
= 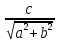 .
.
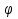 sin x +
sin x + 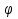 cos x =
cos x = 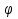 ;
; 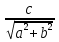 sin x +
sin x + 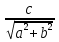 cos x =
cos x = 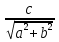 .
.
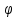 cos
cos sinx + sin
sinx + sin cosx =
cosx = 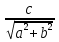 , sin(x +
, sin(x +  ) =
) = 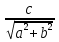 ; x +
; x + = (- 1)n arcsin
= (- 1)n arcsin 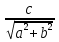 + π n, n
+ π n, n  Z;
Z;
x + = (- 1)n
= (- 1)n  + π n, n
+ π n, n  Z; x = -
Z; x = - + (- 1)n
+ (- 1)n  + π n, n
+ π n, n  Z.
Z.
Эта серия корней распадается на две серии:
при четном n: n = 2m x = - +
+  + 2πm = 2πm, m
+ 2πm = 2πm, m  Z;
Z;
при нечетном n: n= 2k + 1 x = - -
-  + π (2k + 1) = -
+ π (2k + 1) = -  + π + 2πk= =
+ π + 2πk= =  + 2πk, k
+ 2πk, k  Z.
Z.
Ответ. x = 2πn, n  Z; x =
Z; x =  + 2πk, k
+ 2πk, k  Z.
Z.
Или 2)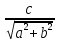 sin
sin sinx + cos
sinx + cos cosx =
cosx = 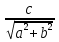 ; cos(x -
; cos(x -  ) =
) = 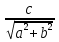 ; x -
; x - = ± arccos
= ± arccos 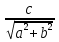 + 2π n, n
+ 2π n, n  Z;
Z;
x - = ±
= ±  + 2π n, n
+ 2π n, n  Z; x =
Z; x = ±
±  + 2π n, n
+ 2π n, n  Z.
Z.
Эта серия корней распадается на две серии: x = 2πn, n  Z; x =
Z; x =  + 2πk, k
+ 2πk, k  Z.
Z.
Ответ. x = 2πn, n  Z; x =
Z; x =  + 2πk, k
+ 2πk, k  Z.
Z.
-
Решение второй группы.
Решение уравнения sin x + cos x = 1 с помощью универсальной тригонометрической подстановки: sin x = 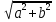 , cos x =
, cos x =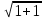 .
.
Перепишем данное уравнение с учетом приведенных формул:
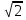 +
+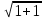 = 1. Умножим обе части уравнения на общий знаменатель
= 1. Умножим обе части уравнения на общий знаменатель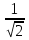 (
(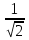 ≠0).
≠0).
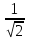 +
+ 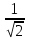 =
= 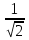 ;
; 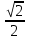 -
- 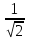 = 0;
= 0; 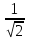 (
(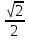 - 1) = 0.
- 1) = 0.
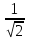 = 0 или
= 0 или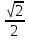 - 1 = 0.
- 1 = 0.
1) 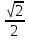 = 0,
= 0,  = πn, n
= πn, n  Z; x = 2πn, n
Z; x = 2πn, n  Z.
Z.
2)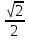 = 1,
= 1,  =
=  + πk, k
+ πk, k  Z; x =
Z; x =  + 2πk, k
+ 2πk, k  Z.
Z.
Ответ. x = 2πn, n  Z; x =
Z; x =  + 2πk, k
+ 2πk, k  Z.
Z.
3. Решение третьей группы.
Решение уравнения sin x + cos x = 1 приведением к однородному уравнению относительно синуса и косинуса.
Используя формулы двойного аргумента sin x = 2sin cos
cos , cosx = cos2
, cosx = cos2  - sin2
- sin2 и записывая
и записывая
правую часть уравнения в виде 1= cos2 + sin2
+ sin2 , получаем:
, получаем:
2sin cos
cos + cos2
+ cos2 - sin2
- sin2 = cos2
= cos2 + sin2
+ sin2 ; 2 sin2
; 2 sin2 - 2sin
- 2sin cos
cos = 0.
= 0.
Вынося 2sin за скобки, получим равносильное уравнение
за скобки, получим равносильное уравнение
2 sin (sin
(sin - cos
- cos 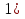 = 0. Произведение равно нулю, если хотя бы один из множителей равен
= 0. Произведение равно нулю, если хотя бы один из множителей равен
нулю, другие при этом имеют смысл. Следовательно, 2sin = 0 или sin
= 0 или sin - cos
- cos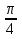
1) sin = 0.
= 0. 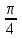 =
= 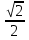 n, n
n, n  Z; x = 2πn, n
Z; x = 2πn, n  Z.
Z.
2) sin - cos
- cos = 0 - однородное уравнение первой степени. Делим обе части уравнения на cos
= 0 - однородное уравнение первой степени. Делим обе части уравнения на cos
(cos ≠ 0, в противном случае, если cos
≠ 0, в противном случае, если cos = 0, то и sin
= 0, то и sin = 0, что противоречит основному
= 0, что противоречит основному
тригонометрическому тождеству cos2 + sin2
+ sin2 = 1).
= 1).
tg 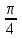 - 1= 0; tg
- 1= 0; tg 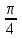 = 1.
= 1.
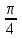 =
=  +
+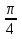 х =
х =  + 2πk, k
+ 2πk, k  Z .
Z .
Ответ. x = 2πn, n  Z; x =
Z; x =  + 2πk, k
+ 2πk, k  Z.
Z.
4. Решение четвертой группы.
Решение уравнения sin x + cos x = 1 с применением формул сложения тригонометрических
функций sin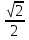 + sin
+ sin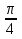 = 2 sin
= 2 sin 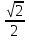 cos
cos 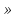 .
.
Выразим cos x через sin x, используя формулы приведения: cos x = sin( - x).
- x).
sin x + sin ( - x) = 1; 2 sin
- x) = 1; 2 sin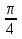 cos
cos 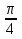 = 1; 2 sin
= 1; 2 sin  cos (x -
cos (x -  ) = 1;
) = 1;
2∙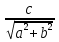 ∙ cos (x -
∙ cos (x -  ) = 1; cos (x -
) = 1; cos (x -  ) =
) =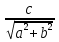 .
.
x -  = ± arccos
= ± arccos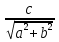 +2
+2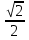 n, n
n, n  Z; x =
Z; x =  ±
±  +2
+2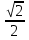 n, n
n, n  Z.
Z.
x = 2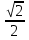 n, n
n, n  Z; х =
Z; х =  + 2
+ 2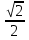 k, k
k, k  Z.
Z.
Ответ. x = 2πn, n  Z; x =
Z; x =  + 2πk, k
+ 2πk, k  Z.
Z.
5. Решение пятой группы.
Решение уравнения sin x + cos x = 1 способом возведения обеих частей уравнения в квадрат.
(sin x + cos x )2 = 1; sin2 x + 2sin x cos x + cos x2 = 1.
Используя формулу синуса двойного аргумента sin 2x = 2sin x cos x и основное
тригонометрическое тождество cos2х + sin2х = 1, имеем:
sin 2x + 1 = 1; sin 2x = 0; 2x = πn, n  Z; x =
Z; x =  , n
, n  Z.
Z.
При возведении уравнения в квадрат получаем уравнение - следствие, поэтому проведем
проверку.
Проверка.
1) При х = 2πn, n  Z, 0 + 1 = 1 верно, х = 2πn, n
Z, 0 + 1 = 1 верно, х = 2πn, n  Z - корни уравнения.
Z - корни уравнения.
2) При х =  + 2πn, n
+ 2πn, n  Z; 1+ 0 = 1 верно, х =
Z; 1+ 0 = 1 верно, х =  + 2πn, n
+ 2πn, n  Z - корни уравнения.
Z - корни уравнения.
3) При х = π + 2πn, n  Z, 0 - 1 = 1 неверно, х = π + 2πn, n
Z, 0 - 1 = 1 неверно, х = π + 2πn, n  Z - не являются корнями
Z - не являются корнями
уравнения.
4) При х = 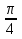 + 2πn, n
+ 2πn, n  Z, -1+ 0 = 1 неверно, х =
Z, -1+ 0 = 1 неверно, х = 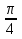 + 2πn, n
+ 2πn, n  Z - не являются корнями
Z - не являются корнями
уравнения.
Ответ. x = 2πn, x =  + 2πn, n
+ 2πn, n  Z.
Z.
6. Решение шестой группы.
Решение уравнения sin x + cos x = 1 с применение формул двойного и половинного
аргумента.
Запишем уравнение в виде: sin x = 1 - cos x .
Сделаем замену: sin x = 2sin cos
cos , 1 - cos x = 2sin2
, 1 - cos x = 2sin2 .
.
2sin cos
cos = 2sin2
= 2sin2 ; 2sin
; 2sin cos
cos - 2sin2
- 2sin2 = 0. Вынося 2sin
= 0. Вынося 2sin за скобки, получим равносильное
за скобки, получим равносильное
уравнение 2sin (sin
(sin - cos
- cos 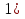 = 0. Произведение равно нулю, если хотя бы один из множителей
= 0. Произведение равно нулю, если хотя бы один из множителей
равен нулю, а другие при этом не теряют смысла.
2sin = 0 или cos
= 0 или cos  - sin
- sin = 0.
= 0.
1) 2sin = 0;
= 0;  = πn, n
= πn, n  Z; x = 2πn, n
Z; x = 2πn, n  Z.
Z.
2) cos = sin
= sin ;
; 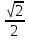 = 1;
= 1;  =
=  + πk; x =
+ πk; x =  + 2πk, k
+ 2πk, k  Z.
Z.
Ответ. x = 2πn, n  Z; x =
Z; x =  + 2πk, k
+ 2πk, k  Z.
Z.
7. Решение седьмой группы.
Решение уравнения sin x + cos x = 1 с применение основного тригонометрического
тождества.
Из тождества sin2 x + cos2 x = 1 имеем cos2 x = 1 - sin2 x, откуда cos x = ±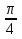 .
.
sin x ±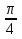 = 1; ±
= 1; ±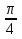 = 1 - sin x; 1 - sin2 x = (1 - sin x)2;
= 1 - sin x; 1 - sin2 x = (1 - sin x)2;
(1- sin x) (1 + sin x) - (1 - sin x)2 = 0; (1- sin x) (1 + sin x - 1 + sin x) = 0; (1 - sin x) ∙ 2sin x = 0.
1 - sin x = 0 или 2 sin x = 0.
1) sin x = 1; x =  + 2πk, k
+ 2πk, k  Z.
Z.
2) sin x = 0; x = πn, n  Z.
Z.
В процессе решения обе части уравнения возводились в квадрат, что могло
привести к появлению посторонних решений, поэтому необходима проверка.
Выполним ее.
При х =  + 2πk, k
+ 2πk, k  Z, 1+ 0 = 1 верно, х =
Z, 1+ 0 = 1 верно, х =  + 2πk, k
+ 2πk, k  Z.- корни уравнения.
Z.- корни уравнения.
При х = 2πn, n  Z, 0 + 1 = 1 верно, х = 2πn, n
Z, 0 + 1 = 1 верно, х = 2πn, n  Z - корни уравнения.
Z - корни уравнения.
При х = π + 2πn, n  Z, 0 - 1 = 1 неверно, х = π + 2πn, n
Z, 0 - 1 = 1 неверно, х = π + 2πn, n  Z - не являются корнями уравнения.
Z - не являются корнями уравнения.
Ответ. x = 2πn, n  Z; x =
Z; x =  + 2πk, k
+ 2πk, k Z.
Z.
8. Решение восьмой группы.
Решение уравнения sin x + cos x = 1 способом приведения к квадратному уравнению
относительно одной из функций.
Рассмотрим основное тригонометрическое тождество sin2 x + cos2 x = 1, откуда следует sin x =
±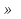 , подставим полученное выражение в данное уравнение.
, подставим полученное выражение в данное уравнение.
±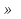 + cos x = 1; ±
+ cos x = 1; ±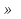 = 1 - cos x.
= 1 - cos x.
Возведем обе части полученного уравнения в квадрат: 1 - cos2x = 1 - 2cos x + cos2x;
2cos2x - 2cos x = 0; cos x (cos x - 1) = 0.
cos x = 0 или cos x - 1 = 0.
1) cos x = 0. x =  + πk, k
+ πk, k  Z.
Z.
2) cos x - 1 = 0; cos x =1. х = 2πn, n  Z.
Z.
Корни необходимо проверить.
При х =  + 2πk, k
+ 2πk, k  Z, 1+ 0 = 1 верно, х =
Z, 1+ 0 = 1 верно, х =  + 2πk, k
+ 2πk, k  Z - корни уравнения.
Z - корни уравнения.
При х = -  + 2πk, k
+ 2πk, k  Z, - 1 + 0 = 1 неверно, х = -
Z, - 1 + 0 = 1 неверно, х = -  + 2πk, k
+ 2πk, k  Z - не являются корнями
Z - не являются корнями
уравнения.
При х = 2πn, n  Z, 0 + 1 = 1 верно, х = 2πn, n
Z, 0 + 1 = 1 верно, х = 2πn, n  Z - корни уравнения.
Z - корни уравнения.
Ответ. x = 2πn, n  Z; x =
Z; x =  + 2πk, k
+ 2πk, k Z.
Z.
9. Решение девятой группы.
Решение уравнения sin x + cos x = 1 графическим способом
Перепишем уравнение в виде: sin x = 1 - cos x.
Построим в одной системе координат графики функций: у = sin x , y =1 - cos x.
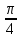
Абсциссы точек пересечения являются решениями данного уравнения.
Из графика видно, что уравнение имеет 2 решения: x = 2πn, n  Z; x =
Z; x =  + 2πk, k
+ 2πk, k  Z. (Необходимо обязательно проверять это вычислениями).
Z. (Необходимо обязательно проверять это вычислениями).
Ответ. x = 2πn, n  Z; x =
Z; x =  + 2πk, k
+ 2πk, k  Z.
Z.
Итог урока.
Учащиеся научились решать тригонометрические уравнения вида a sin x + b cos x = c, освоили новый материал.
На примере одного уравнения рассмотрели несколько способов решения.
Учащиеся были непосредственными участниками урока, была задействована обратная связь в системе ученик-учитель.
Учащиеся получили навыки самостоятельной работы с дополнительной литературой.
Литература.
1. Материалы курса «Тригонометрия в школе». /Н.Н. Решетников, М. Педагогический университет «Первое сентября», 2010 г.
2. Математика. Большой справочник школьников и поступающих в вузы. М.»дрофа»,1999 г.
3. Математика. Учебное пособие для слушателей подготовительных курсов. Новочеркасск, НГМА,2003 г.
4.Алгебра и начала анализа. 10 -11 классы: учебник для общеобразовательных учреждений: базовый уровень/ Ш.А. Алимов и др./ - М, Просвещение, 2010 г.
Интернет- ресурсы
1.›
2.festival.1september.ru/articles/515874/