Конспект урока по математике для 8 класса 'Решение квадратных уравнений'

Конспект урока алгебры в 8 классе.

Тема: «Решение квадратных уравнений»

Тип урока: урок обобщения и систематизации знаний.

Цели урока:

• Образовательные: систематизировать знания, выработать умение выбирать рациональный способ решения квадратных уравнений и создать условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений.

• Развивающие: формировать учебно-познавательные навыки по работе с дополнительным материалом, развивать логическое мышление, внимание, общеучебные умения;
  
  

• Воспитательные: воспитывать интерес к математике, активность, мобильность, взаимопомощь, умение общаться.

Ход урока:

1.Организационный момент.

Сегодня на уроке мы систематизируем знания о методах решения квадратных уравнений, закрепим навыки решения квадратных уравнений.

2. Фронтальная работа с классом.

Цель : повторение теоретического материала.

1. x² + 9x - 12 = 0;

2. 4x² + 1 = 0;

3. x² -2x + 5 = 0;

4. 2z² - 5z + 2 = 0;

5. 4y² = 1;

6. -2x² - x + 1 = 0;

7. x² + 8x = 0;

8. 2x²=0;

9. -x² - 8x=1

10. 2x + x² - 1=0

Вопросы учащимся:

1. Дайте определение квадратного уравнения.

2. Назовите виды квадратных уравнений.

3. Запишите номера приведенных квадратных уравнений, записанных на доске.

4. Запишите номера неполных квадратных уравнений, записанных на доске.

5. Запишите номера полных квадратных уравнений, записанных на доске.

6. По какому признаку мы можем отнести квадратное уравнение к тому или иному виду?

7. Как называются коэффициенты квадратного уравнения?

8. Запишите квадратное уравнение, у которого свободный член равен 6, первый коэффициент равен 1, а второй, равен -12. Как оно называется?

9. От чего зависит количество корней квадратного уравнения?

10. Впишите вместо пропуска такой коэффициент, чтобы квадратное уравнение

2х²-8х+....=0 не имело корней.

11. Изменятся ли корни уравнения 2x² +5x +7=0, если у него изменить знак:

- одного коэффициента

- трёх коэффициентов.

3.Математический диктант.

Задание. Проанализируйте высказывания. Зачеркните в таблице буквы, обозначающие ложные высказывания (номер высказывания совпадает с порядковым номером буквы). Из оставшихся букв получите слово.

1. Уравнение x²+9=0 имеет два корня.

2.В уравнении x²-2x+1=0 единственный корень.

3. В уравнении x²-5x+3=0 сумма корней равна - 5.

4. В уравнении x²+3x=0 один из корней - отрицательное число.

5. В уравнении x²=0 дискриминант равен 0.

6. Уравнение x²-8x-3=0 не имеет корней.

7. Корнями уравнения x²-100x+99=0 являются числа 99 и 1.

8. Произведение корней уравнения x²-11x+9=0 равно - 9.

9. Корни уравнения x² - 0,16 = 0 равны .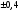

10. Уравнение x²-9x+8=0 является неполным.

11. Если дискриминант уравнения - число отрицательное, то уравнение не имеет корней.

12. Корни уравнения x²-4х =0 являются противоположными числами.

13. Уравнение x² =0 имеет один корень.

1

2

3

4

5

6

7

8

9

10

11

12

13

М

О

Д

Т

Л

Р

И

К

Ч

Г

Н

А

О

В результате вычёркивания букв должно получиться: ОТЛИЧНО

4. Повторение теоремы Виета.

Скажите, какая теорема используется для того чтобы сразу, не производя вычислений, ответить на вопрос: «Чему равна сумма и произведение корней квадратного уравнения?»

(Один человек у доски записывает формулы теоремы Виета).

А)Устно: найти корни уравнения по теореме:

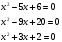(ответы: 3 и 2; 4 и 5; -2 и -1)

Б)Теорема Виета находит широкое применение и в уравнениях вида

aх² + bх + с = 0.

Использование некоторых свойств даёт значительные преимущества для быстрого получения ответа при решении квадратных уравнений.

Рассмотрим эти свойства:

1) a + b +с = 0 х₁ = 1, х₂ = с/а.

5х² + 4х - 9 = 0; х₁ =1, х₂ = - 9/2.

2) а - b + с = 0 х₁ = - 1, х₂ = - с/а.

Например: 4х² + 11х + 7 = 0; х₁ = - 1, х₂ = - 7/4.

3) ав +с0

Устно решить уравнение: х² + bх + ас = 0

Его корни разделить на а.

а) 2х² - 11х + 5 = 0.

Решаем устно уравнение: х² - 11х + 10 = 0. Его корни 1 и 10. Делим на 2.

Тогда х₁ = 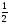, х₂ = 5.

Ответ: 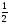; 5.

в) 6х² -7х - 3 = 0

Решаем устно уравнение: х² -7х - 18 = 0. Его корни -2 и 9. Делим на 6.

Тогда х₁ = - 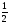, х₂ = .

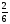Ответ: -; .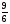

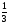Решите уравнения, используя эти свойства по вариантам:

I вариант.

1) 14х² - 17х + 3 = 0

2) х² - 39х - 40 = 0

3)100х² - 83х - 18 3= 0

II вариант.

1) 13х² - 18х + 5 = 0

2)х² + 23х - 24 = 0

3)100 х² + 97х - 197 = 0

5.Итог урока.

6. Домашнее задание.

п.21,22, 24, № 654, № 672(а,б), на «5» - № 679.