- Учителю
- Дидактический материал по математике 5-9 класс
Дидактический материал по математике 5-9 класс
Приложение № 1.
Матрица параметров учебного успеха ученика N
(характеристика его индивидуального стиля учебной деятельности - ИСУД)
Фамилия, имя
Обученность
Обучаемость
Внимание
Память
Модальность
Полушарие
Коммуникативные ОУУН
Организа-ционные ОУУН
Информа-ционные ОУУН
Мыслительные ОУУН
Уровень мотивации
Объем
Объем
Распределен.
Концентрац.
Устойчив.
Слов/лог.
Слов./лог.
Нагл/образ.
Эмоцион.
Монологич.
Акт.слушан.
Диалог
Работа в гр.
Планиров.
Самооценка
Раб.мес.тет
Смысл.чтен
Свор.инфор
ТСО
Анализ
Синтез
Сравнение
Логика
Вывод
N
5
III
виз
равно
Соц
4
II
ауд
лево
Поз
3
I
кин
право
баз
Три ряда клеток соответствуют трем уровням развития психофизиологических функций и общеучебных навыков:
Нижний ряд - недостаточный уровень; средний ряд - достаточный; верхний уровень - оптимальный.
Используемая литература
1. Галеева Н.Л., Мельничук Н.Л.
Сто приемов для учебного успеха ученика на уроках географии: Методическое пособие для учителя по освоению и использовании педагогической технологии «ИСУД» - дидактического ресурса личностно ориентированного образовательного процесса. - М.: «5 за знания», 2006 - 126 с. («Методическая библиотека
Приложение № 2.
Приемы по математике: 5 класс
1.Прием № 7 . Тема: Действия с десятичными дробями. 5 класс. Кольцевые примеры. Запиши ответ и реши выражение
-
16,38+2,064=
-
… - 12,704=
-
… x 2,2=
-
… : 4=
-
3,157 +...=
-
18 - …=
-
0,2 x …=
-
… : 0,0001=
-
12,48+6,306=
-
… - 3,286=
-
… x 2,2=
-
… : 5=
-
6,82 + …=
-
17 - …=
-
0,2 x …=
-
… : 0,0001=
2.«Проверь и оцени»
Математика - 5
Тема «Сравнение натуральных чисел»
1. 1986 > 993;
2. 305 286 < 327 158;
3. 65 287 115 > 652 987 115;
4. 86345167603 >86345197603;
5. 110100101 < 1001101001;
6. 21*** < 23***;
7. **412 > **9*;
8. **** > ** ***;
9. 950** > *4
3.Прием № 2. Тема: Деление десятичных дробей, этап актуализации знаний.
В таблице указано название продукта и содержание в нем витамина С в миллиграммах на 100 грамм продукта
Название продукта
Содержание витамина С
слива
5
яблоко
7
банан
12
вишня
15
ананас
20
апельсин
40
земляника
60
черная смородина
300
а) определите содержание витамина С в граммах на 1 кг продукта
б) сколько витамина С содержится:
-
В 1 апельсине (1 кг - 4 шт.)
-
В 1 ягоде черной смородины (1 кг - 950 шт.)
-
В 1 сливе (1кг - 75 шт.)?
Восстановите запятые в примерах:
а) 3,2 + 18 = 5 г) 7,36 - 336 = 4
б) 3 + 1,08 = 408 д) 63 - 27 = 603
в) 42 + 17 = 212 е) 57 - 4 = 17
Восстановите запятые в примерах:
а) 32 + 18 = 5 г) 736 - 336 = 4
б) 3 + 108 = 408 д) 63 - 27 = 603
в) 42 + 17 = 212 е) 57 - 4 = 17
Найдите ошибки:
1) 3,48![]() 3,6 2) 0,45
3,6 2) 0,45 ![]() 0,4
0,4
3) 42,14 ![]() 42,2 4) 4,712
42,2 4) 4,712 ![]() 2 ,2
2 ,2
5) 7,88 ![]() 6) 0,0059
6) 0,0059 ![]() 0, 005
0, 005
5.Приём № 7 Тема: Деление десятичных дробей на натуральное число, этап диагностики умений и знаний.5 класс
Найдите ошибку и запишите правильное решение
а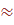
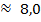
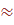
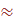
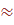
 ) 1,083 б) 2,3 4 в) 0,12 8 г) 20,15 5
) 1,083 б) 2,3 4 в) 0,12 8 г) 20,15 5







 * 5 2 0 5,75 8 0,15 20 4,3
* 5 2 0 5,75 8 0,15 20 4,3


 3 0 40 15
3 0 40 15
2 8 40 15



 2 0 0 0
2 0 0 0
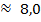 2 0
2 0
0
6. Прием № 13а . математика 5 класс, тема: Сравнение десятичных дробей.
Выясните, в каком столбике верно записано число. Напишите в кружке букву, ему соответствующую
-
Пять целых две десятых
5,02
5,2
5 ,002
,002
т
р
п
-
Ноль целых восемь тысячных
0,008
0,08
0 ,8
,8
о
е
у
-
Три целых двадцать пять тысячных
3,25
30,25
3 ,025
,025
д
в
т
4) шестнадцать целых пять сотых
16,005
16,5
1 6,05
6,05
а
е
о
5) восемнадцать целых восемь сотых
18,8
18,08
18,008
ш
к
в
6) пять целых пятнадцать пятитысячных
5,0015
5,015
5,15
а
у
и
7) тридцать четыре целых сто пять тысячных
34,0105
34,105
3 4,15
4,15
в
с
м
7. Тема: Упрощение выражений, прием № 10
М атематический диктант
атематический диктант
-
Решите уравнение
6х = 216
1.Решите уравнение
5х = 125
-
Решите уравнение
-
: х = 10
2.Решите уравнение
140 : х = 14
3.Вычислите
-
* 7 + 37 * 7
3.Вычислите
163 * 7 - 7 * 63
4.Упростите
Х*4*5
4.Упростите
2 * Х*3
5.Переместительное свойство умножения
5.Переместительное свойство сложение а + в =
6.Сочетательное свойство сложения
6.Сочетательное свойство умножения (а + в) + с =
7.Распределительное свойство умножения относительно вычитания.
7.Распределительное свойство умножения относительно сложения. (а + в) *с =
Математика 6 класс
-
Прием № 20 Тема: Раскрытие скобок. 6 кл. Игра: Домино.
-
3(х+1)-4(х-2)
3х+3-4х+8
(а+2b)+(2a+b)
a+2b+2a+b
(4a-2b)-(3a+b)
4a-2b-3a-b
(3y-x)-(-y+x)
3y-x+y-x
(2x+2y)-(2x-2y)
2x+2y-2x+2y
2(x-1)+3(x-2)
2x-2+3x-6
(x-y)+(-2x-2y)
x-y-2x-2y
4(a+2b)-3(a-2b)
4a+8b-3a+6b
-
Прием № 11. Тема: Координатная плоскость. Тест
Продолжите предложения:
-
Координатной плоскостью называется плоскость, на которой ……
-
Систему координат образуют …….
-
Координатная прямая х называется …..
-
Координатная прямая у называется ……
-
Точка пересечения прямых х и у называется ….
-
Пара чисел, определяющая положение точки на плоскости , называется …
-
Первая координата называется …
-
Вторая координата называется …
-
Прием № 33. Тема: Коэффициент.
-8,4х2у3
1,2а2у2
-d
![]() m5
m5
-![]() k2t
k2t
![]() a3
a3
-ab
-2,1x
1,1m2n
-
Из первой строки выберите выражение, числовой коэффициент которого является наименьшим.___________________
-
Из второй строки выберите выражение, числовой коэффициент которого является наибольшим. ___________________
-
Из третьей строки выберите выражение, числовой коэффициент которого больше -1,2 и меньше 1. ____________________
-
Найдите разность коэффициента первого выбранного выражения и суммы коэффициентов второго и третьего выражений.
-
Прием № 33. Тема: Коэффициент.
Карточка из серии «История космонавтики»
Он родился 22 августа 1930 года в деревне Першутино Клинского района Московской области. В 1950 - 1954 годах служил в Тамбове в военном авиационном радиотехническом училище ВВС (ныне ТВАИИ). 3 - 19 июля 1974 года осуществил полет в космос на орбитальной научной станции «Салют - 3», за что ему было присвоено звание Героя Советского Союза. Затем работал в Центре подготовки космонавтов.
О ком идет речь?
а) -0,2х·(-4)= -0,08; б) -0,4у·(-0,8)= -0,96;
в) -0,2·(-0,7х)=0,84; г) 1,2·(-0,6у)=-2,88;
д) ![]() ·2,8у·(-0,6)=1,44; е) -
·2,8у·(-0,6)=1,44; е) -![]() х·(-3,6)·2,1=20,16;
х·(-3,6)·2,1=20,16;
ж) 2![]() у· (-
у· (-![]() )·1,6=6,6.
)·1,6=6,6.
Для ответа на данный вопрос:
1) решите уравнения;
2) из предложенных ниже букв выберите те, которые соответствуют полученным решениям;
3) составьте фамилию летчика - космонавта.
3
-0,1
3,3
6
-3
2
4
0,1
-3,3
-2
и
а
л
т
р
м
ю
и
н
х
ФАМИЛИЯ____________________________________________________
-
Прием № 35. Тема: Взаимно простые числа.
Заполните пропуски в предложениях.
1) Числа а и b называют ________________________, если НОД (а; b)=1.
2) Неравные 1 числа ____________ являются взаимно простыми делителями 12.
3) Составные числа 60 и ___________ взаимно простые.
4) Наименьшим общим кратным двух простых чисел c и d является ___________.
5) Если НОК (х; у)=18, а НОД (х; у)=3, то ху=_____.
6) Если а=2×3×5, b=7×11×13, то НОК (а;b)=______.
7) Число d делится на 5, число d делится на 7, значит, оно делится на __________.
8) Произведение двух различных простых чисел имеет _____________ делителей.
9) На 15 делятся те, и только те числа, которые _____________________________
-
Прием № 5а. Тема: действия с рациональными числами.
Выбрать правильно закодированные ответы.
13 - (-6)
Б
19
-6 + (-42)
О
-48
-5,4 + 8,9
Г
3,5
-5 / 8 - (-7/8)
А
1/4
-8![]() + 4
+ 4 ![]()
Т
-4 ,4
-13 + ( -![]() )
)
О
-![]()
-7 3/4 + 0,75
Е
-7
2 1/2 * (-2/5)
О
-1
-3 : 6/7
З
-3,5
-6/11 : (-3/22)
Е
4
-1/7 * (-7/9)
Р
1/9
![]() * (-
* (-![]() )
)
О
-6
7. Прием № 7. Тема: Сокращение дробей.
1. Сократите дроби и установите соответствие между названием и изображением редких цветковых растений, внесенных в Красную книгу НАО.
![]()
Фиалка наскальная

![]()
![]()
Стерис альпийский

![]()
![]()
Родиола розовая
![]()
![]()
![]()
Купальница открытая

![]()
![]()
Мак полярный

![]()
![]()
Минуарция крупноплодная
![]()
![]()
![]()
Мытник прелестный

![]()
![]()
Пион уклоняющийся

![]()
8. Прием № 6е .Тема: Нахождение дроби от числа.
Заполни таблицу: под каждым числом запишите указанную его часть
400
160
24
8
1
![]()
![]()
![]()
![]()
![]()
0,5
1%
10%
25%
-
Прием № 35.Тема: Сложение и вычитание смешанных чисел.
Заполни пропуски:
а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
д) ![]() е)
е) ![]()
Сделай вывод: как вычитать дробные числа из целых.
«Проверь и оцени»
Тема «Сокращение обыкновенных дробей»
1. ![]() ; 2.
; 2. ![]() ;
;
3. ![]() ; 4.
; 4. ![]() ;
;
5. ![]() ; 6.
; 6. ![]() ;
;
7. ![]() ; 8.
; 8. ![]() ;
;
9. ![]() ; 10.
; 10. ![]() ;
;
11. ![]() ;
;
12. ![]() .
.
Алгебра 7 класс
1.Прием № 8. Тема: Формулы сокращенного умножения.
Тест с выбором правильного ответа. Вариант 1
В примерах 1-5 раскройте скобки:
1. (х + 2у) 2
А. х2 + 4ху + Ау2 В. x2 + 4у2.
Б. x2 + 4ху + 2y2. Г. x2 + 2ху + 2x2.
2. (2а - З)2.
А. 4а2-6а + 9. В. 2а2 - 12а+ 9.
Б. 4а2-12а+ 9. Г. 4а2-9.
3. (Зх - 5у2) (Зх + 5у2).
А. 9х2 - 25у2. В. 9x2+ 25у2
Б. 9х2 + 25y4. Г. 9x2 - 25у4
4. (а + 2) (а2 - 2а + 4).
А. а3+16. В. а3 + 2а2 + 8.
Б. а3-8. Г. а3+ 8.
A. x3 + x2-1. B.x3-x2-1.
Б.x8-1. Г.х8+1.
6. Даны два равенства:
-
(2а - 3b2)2 = 4а2 - 6аb2+ 9b4;
-
(х + Зy)2 = x2 + 9y2 + 6xy.
Какое из них верно (да), а какое неверно (нет)?
А. Да, да. Б. Да, нет. В. Нет, да. Г, Нет, пот.
7. Не решая пример, скажите, корректно (да) или некорректно (нет)
следующее задание:
-
Разделите многочлен Зх2у - 9ху2 на одночлен Зх2у.
-
Разделите многочлен Зхуz - 9xy2z на одночлсш 3y.
А. Да, да. Б. Да, нет. В. Нет, да, Г, Нет, нет.
Вариант 2
В примерах 1-5 раскройте скобки:
1. (За + Ь)2.
А. 9а2 + b2 В. 9а2 + 3ab + b2.
Б. 9а2 + 6аb + b2. Г. За2 + 6ab + b2.
2. (За - 2)2.
А. 9а2 - 6а + 4. В. 9а2 - 12а + 4.
Б. За2-12а+ 4. Г. 9а2-4.
3. (2х - 3y2) (2х + Зy2).
А. 4х2 - 9у2. В. 4x2 + 9y2.
Б. 4х2 - 9у4. Г. 4х2
4. (а - 2) (а2 + 2а + 4).
А. а3-8. Б. а3+ 8. В. а3-2а2+ 8. Г. а3 - 16.
5. (х + 1) (х2 - х +1).
А. x3 + х2-1. Б. x3-1. В. х3-х2-1. Г. x3 + 1.
6. Даны два равенства:
-
(Зx2 + 2у)2 == 4у2 + 12х2у + 9x4;
-
(За - b)2 = 9а2 + b2 - 6аb.
Какое из них верно (дa), a какое неверно (нет)?
А. Да, да. Б. Да, нет. В. Нет, да. Г. Нет, нет.
7. Не решая пример, скажите, корректно (да) или некорректно (нет)
следующее задание:
-
Разделите многочлен 4a3b -8a2b на одночлен 2аb2.
-
Разделите многочлен 5аbс - 10 ab2c3 на одночлен 5a2b.
А. Да, да. Б. Да, нет. В. Нет, да. Г. Нет, нет.
2.Тема: Одночлен и его стандартный вид.
Тест с выбором правильного ответа и самопроверкой, самооценкой. Прием № 8
Вариант 1
1.Упростите выражение - 2(3а - 4) - 3(1+2а) + 2а
а) -10а - 11 б) 2а + 5 в) 5 - 10а
2.Решите уравнение 2а - 3 = 2,5а - 1
а) 8 б) - 4 в) - 1
3. Найдите значение функции у = ![]() х - 3 при х = - 1,5
х - 3 при х = - 1,5
а) - ![]() б) -3,5 в) -
б) -3,5 в) - ![]()
4. Укажите координаты точки пересечения графиков функций
у = - 0,5х + 2 и у = - 3 + 2х
а) (-2; -1) б) (-2; 1) в) ( 2; 1)
5. Найдите значение выражения ![]() ·
·![]()
а) ![]() б)
б) ![]() в)
в) ![]() .
.
6.Упростите выражение ![]()
а) ![]() б)
б) ![]() в)
в) ![]()
7. Вычислить ![]()
а) 8 б)2 в) 1.
8.Расположите по возрастанию числа 2300; 3200; 5100.
а) 5100; 2300; 3200
б) 3200; 2300; 5100
в) 2300; 3200; 5100
9.Преобразуйте в одночлен стандартного вида 24а3в5с5 : (- 0,8ав3с5)
а) -30а2в2с б) - 30а2в2 в) 3а2в2.
10.Найдите значение выражения -2х2 + 3х + 4при х = - 0.5.
а) - 3,5 б) - 2 в) 2
11. Упростите выражение 4х - 2х ( х2 - х + 2)
а) - 2х3 + 2х2
б) -2х3 - 2х
в) - 2х3 -2х2 +8х.
12. Решите уравнение 4х (1+х) - 2х (2х + 3) = 3 - х
а) - 1 б) - 3 в) 3
Вариант 2
1.Упростите выражение 3( 2а - 5) - 4( 1 - 3а) +5а
а) 23а - 19 б) - а - 19 в) а+19.
2.Решите уравнение 1,5т+4 = 2т +1
а) 6 б) - 6 в) 1,5.
3. Найдите значение функции у = - 0,6х - 2 при х = ![]()
а) - 2,4 б) -1,6 в) 2,4.
4.Укажите координаты точки пересечения графиков функций
у = 4 - 0,5х и у = 1,5х - 2
а) (3; 2,5) б) ( -3; - 6,5) в) ( 0,5; -2)
5. Найдите значение выражения ![]()
![]()
а)![]() б)
б) ![]() в)
в) ![]() .
.
6.Упростите выражение ![]()
а) ![]() б)
б) ![]() в)
в) ![]()
7. Вычислить ![]()
а) 81 б) 27 в) 9.
8.Преобразуйте 16а5в3с2 : (- 0,4а3вс) в одночлен стандартного вида
а) -40а2в2с б) - 40а2в2 в) 4а2в.
9.Найдите значение выражения - 4х2 - 2х + 5 при х = - 1,5
а) 1 б) - 1 в) 17
10. Упростите выражение 3х - 2х ( х2 - 2х + 1,5)
а) - 2х3 - 4х2
б) -2х3 + 4х2
в) х3 - х2 + 6х.
11. Решите уравнение 2х (5+3х) - х (6х - 2 ) = 2х- 4
а) - 1,5 б) 1,5 в) - 0,4
12.Расположите по убыванию числа 4300; 6200; 24100.
а)4300; 24100; 6200
б) 6200; 24100; 4300
в) 4300; 6200; 24100
Критерии оценивания:
7-8 заданий - «3»
9-10 заданий - «4»
11-12 заданий - «5»
Ответы
1
2
3
4
5
6
7
8
9
10
11
12
Вариант 1
в
б
в
в
б
в
в
а
б
в
а
б
Вариант 2
а
а
б
а
в
а
в
а
б
б
в
в
-
Прием № 5а. Тема: Формулы сокращенного умножения.
Составь слово.
«Поляна соответствий»
-
№ формулы
формула
№ ответа
ответ
буква
1
(x+3)²
1
4x²-9
О
2
x²-16
2
16x²-40xy+25y²
А
3
(2x-3)(2x+3)
3
(x-4)(x+4)
И
4
81-18x+x²
4
(3y+6x)²
Т
5
(4x-5y)²
5
x²+6x+9
Д
6
25x²-49y²
6
(9-x)²
Ф
7
9y²+36yx+36x²
7
(5x-7y)(5x+7y)
Н
4. Прием № 17а. Тема: Формулы сокращенного умножения.
-
1. Найди ошибку в каждой формуле и исправь её:
1.(4у-3х)(4у+3х)=8у²-9у²
2.100х²-4у²=(50х-2у)(50х+2у)
3.(3х+у)²=9х²-6ху+у²
4.(6a-9c)²=36a²-54ac+81c²
5.х³+8=(х+2)(х²-4х+4)2. Восстанови формулы, заменив звездочки правильными выражениями:
1) b²+20b+*=(*+*)²
2)16m²-*= (*-8m)(*+8m)
3) (*+3x)²=49y²+*+*
4) (3a+*)(3a-*)=*-81
5) (5x-*)²=*-*+16
5.
-
«Проверь и оцени»
Тема «Формулы сокращённого умножения»
1. (4а +10)(10 - 4а) = 16а2-100 ;
2. (с + у)2 = с2 + у2;
3. а2 + 12а+ 36 = (6 + а)2 ;
4. (2у - 7а)(2у + 7а) = 2у2 - 7а2;
5. х2 - 2х + 4 = (х - 2)2;
6. 9 - а6 = (а3 + 3)(3 - а3);
7. (3с3 - 4)2 = 9с9 - 24с + 8;
8. 5х2 - 2у2 = (5х - 2у)(5х + 2у);
9. х2 + а2 = (х + а)2;
10. 4х2 - 1 = (2х - 1)2;
11. 25а2 +10ау +4у2=(5а+2у)2.
Геометрия 7 класс
1.Прием № 17в. «Проверь и оцени».
Тема «Свойства углов, образованных двумя параллельными прямыми и секущей»
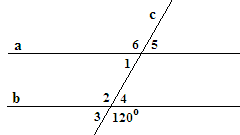
На рисунке a ║ b, с - секущая
1. ![]() 1 и
1 и ![]() 4 - накрест лежащие;
4 - накрест лежащие;
2. ![]() 5 и
5 и ![]() 4 - односторонние;
4 - односторонние;
3. ![]() 3 и
3 и ![]() 1 - соответственные;
1 - соответственные;
4. ![]() 1 +
1 + ![]() 2 = 180о; 5.
2 = 180о; 5. ![]() 6 = 120о;
6 = 120о;
6. ![]() 2 =
2 = ![]() 6 7.
6 7. ![]() 1 = 60о;
1 = 60о;
8. ![]() 2 +
2 + ![]() 5 = 180о; 9.
5 = 180о; 9. ![]() 4 +
4 + ![]() 5 = 120о.
5 = 120о.
Тема «Сумма углов треугольника» 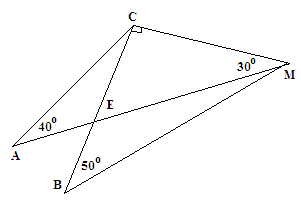
1. ![]() CEM = 60o; 2.
CEM = 60o; 2. ![]() ACM = 110o ;
ACM = 110o ;
3. ![]() АСЕ = 20о ; 4.
АСЕ = 20о ; 4. ![]() СМВ = 40о
СМВ = 40о
5. ![]() ВМЕ = 10о ; 6.
ВМЕ = 10о ; 6. ![]() AEC = 120o .
AEC = 120o .
-
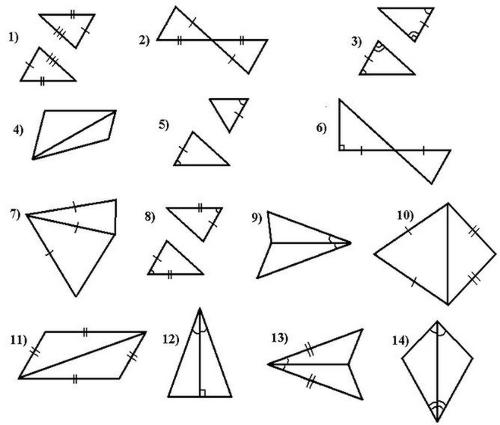
Прием№ 7, Тема: Признаки равенства треугольников.
На рисунках, приведённых ниже, треугольники равны по одному из признаков равенства треугольников. Укажите номера в соответствующей строке ответов.
Ответ:
а) по первому признаку равны треугольники под номерами __________________________
б) по второму признаку равны треугольники под номерами __________________________
в) по третьему признаку равны треугольники под номерами ___________
Алгебра 8 класс
-
Прием № 17а. Тема: Квадратный корень из степени.
Найди ошибку
-
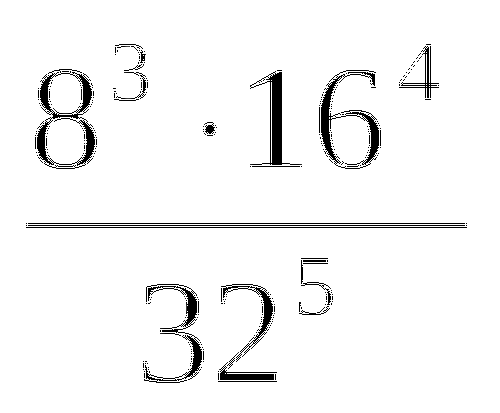 •
•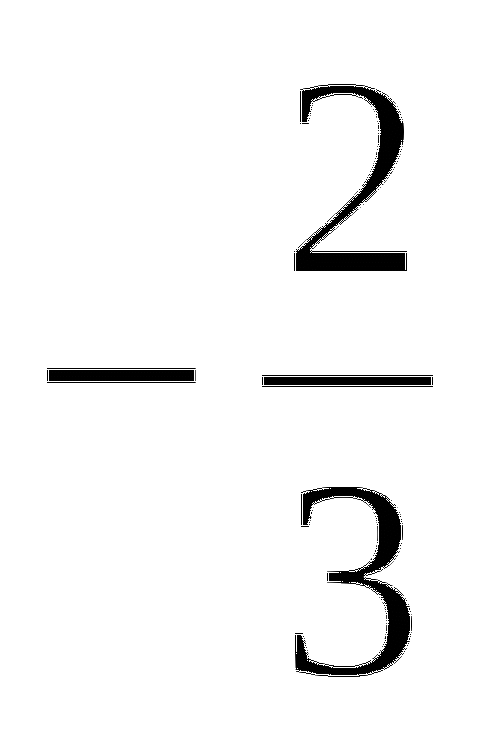 = 0,9
= 0,9 -
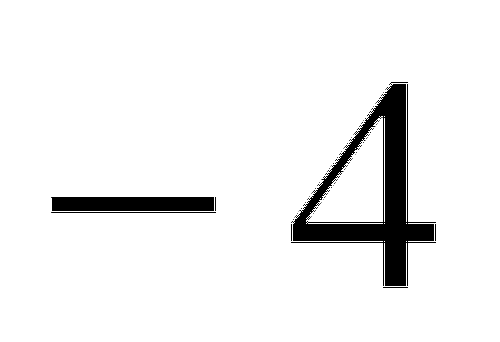 = - 1,3
= - 1,3 -
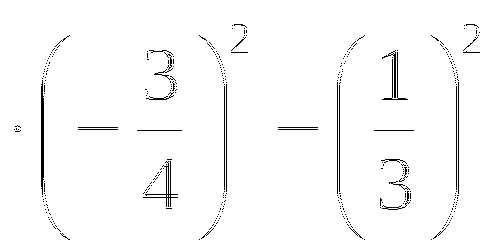 - 0,64 = 0,7
- 0,64 = 0,7 -
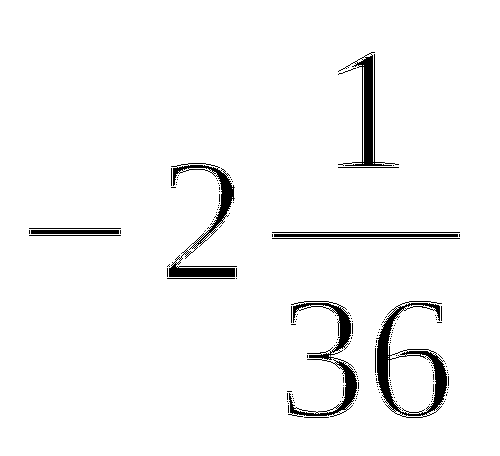 =
= 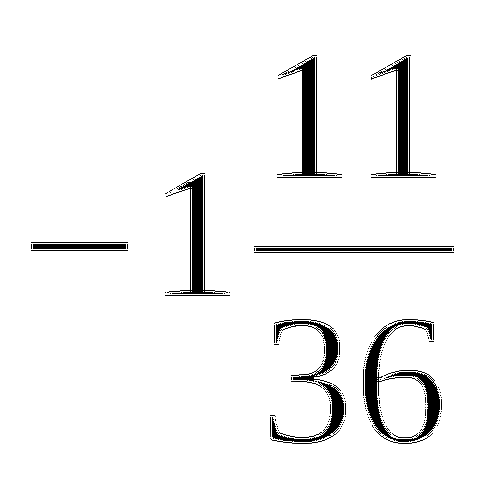
-
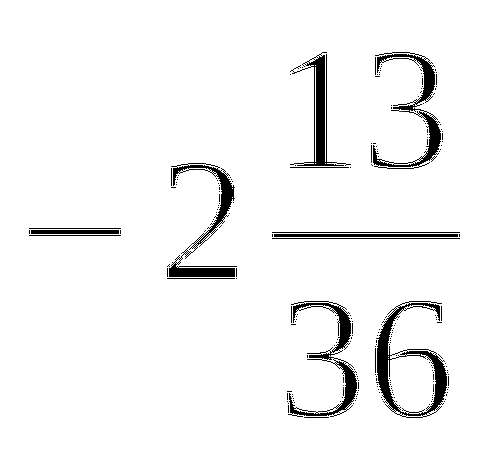 = 13
= 13 -
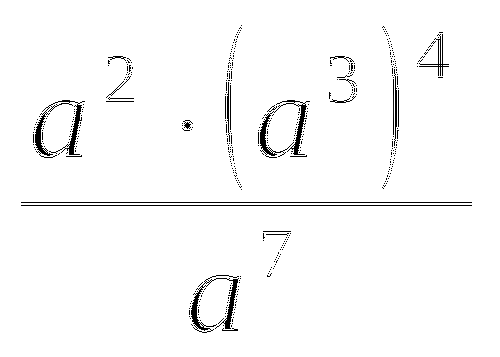 =
= 
Выпиши номера верных равенств.
-
Прием № 5в. Преобразование выражений, содержащих квадратные корни.
Устранение неисправностей в автомобиле.
Учащимся даётся устное задание решить примеры (с выбором правильного ответа).
В результате они узнают, что требуется починить или заменить в автомобиле, чтобы он был готов к гонкам.
1-я группа
1. ![]() 0, 64 * 25
0, 64 * 25
ccc
г) 0,4
ccc
к) 4
2. ![]() 25 * 16 * 0,36
25 * 16 * 0,36
а)12
о)1,2
3. ![]() 2500 * 49
2500 * 49
с) 3500
р)350
4. ![]() 2 * O 18
2 * O 18
п) 9
б) 6
5. ![]() 54/9
54/9
ю) 21/3
у) 12/3
6. ![]() 3 8
3 8
т) 12
р) 81
7. 0,1 ![]() (- 73) 2
(- 73) 2
а) 7,3
и) - 7,3
8. ![]() 4,8
4,8
к) 0,4
т) 4
![]() 0,3
0,3
9. ![]() 3 4 * 20 2
3 4 * 20 2
о) 180
а) 120
10. ![]() 1/11 *
1/11 * ![]() 11/13 *
11/13 * ![]() 13/25
13/25
р) 1/5
с) 1/25
(Карбюратор)
2-я группа
1. ![]() 0,09 * 0,25
0,09 * 0,25
т) 0,15
п) 0,015
2. ![]() 2,69 * 0,04 * 0,0001
2,69 * 0,04 * 0,0001
ccc
о) 0,0026
ccc
и) 0,026
3. ![]() 3 *
3 * ![]() 48
48
ш) 11
р) 12
4. ![]() 3 6/25
3 6/25
м) 1 4/5
л) 13/5
5. ![]() 2 6 * 5 2
2 6 * 5 2
а) 30
о) 40
6. ![]() ( - 0,2) 6
( - 0,2) 6
з) 0,008
ж) - 0,008
7. ![]() 3/7 *
3/7 * ![]() 7 *
7 * ![]() 1/3
1/3
а) 1
ы) - 1
(Тормоза)
3-я группа
1. ![]() 9 * 36
9 * 36
ccc
н) 18
ccc
м) 16
2. ![]() 6,25 * 0,16
6,25 * 0,16
о) 0,1
а) 1
3. ![]() 2 7/9
2 7/9
с) 1 2/3
з) 1 1/3
4. ![]() 3 4 * 6 2
3 4 * 6 2
о) 54
и) 18
5. ![]() ( - 3) 10
( - 3) 10
з) -243
с) 243
(Насос)
-
Прием № 35. Тема: Теорема Виета. Квадратное уравнение.
Вариант 1:
-
Если ах2 + вх + с = 0 - квадратное уравнение, то а называют ____ коэффициентом, в ___ коэффициентом, с ___ членом;
-
Корни квадратного уравнения ах2 + вх + с = 0 вычисляются:
-
Д = в2 - 4ас, Д > или = 0;
-
х1 =
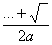 ;
; -
х2 =
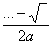
-
Квадратное уравнение вида х2 + рх + g = 0 называют _____;
-
Теорема Виета утверждает, что в уравнении вида
-
-
х2 + рх + g = 0;
-
х1 + х2 = ____;
-
х1 * х2 = ____;
Вариант 2:
-
Если ах2 + вх + с = 0 квадратное уравнение, то:
- первый коэффициент - это число ___;
- второй коэффициент - это число ___;
- свободный член - это число ___;
-
Корни квадратного уравнения ах2 + вх + с = 0 вычисляются
Д = в2 - 4ас;
Д ![]() , то х1 =
, то х1 = ![]() ;
;
х2 =![]() ;
;
-
Приведённое квадратное уравнение - это уравнение вида _____;
-
Теорема Виета утверждает, что в уравнении :
-
х2 + рх + g = 0;
-
х1 + х2 = ____;
-
х1 * х2 = ____;
-
4.
-
«Проверь и оцени»
Тема «Свойства арифметического квадратного корня»
1.
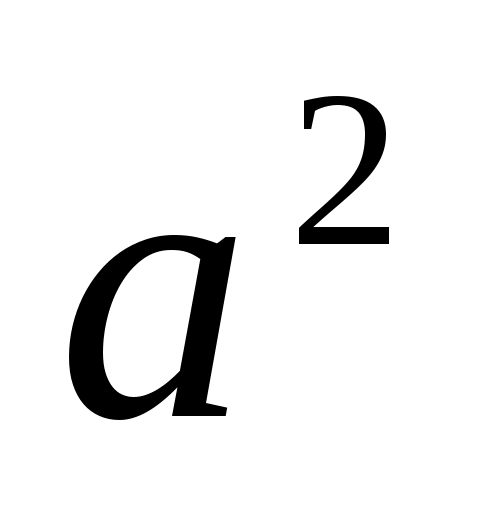 ; 2.
; 2.  ;
; 3.
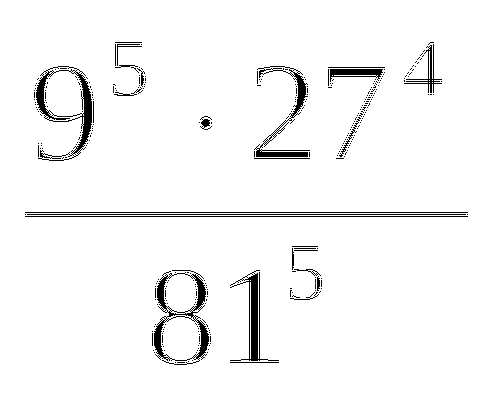 ; 4.
; 4.  ;
; 5.
 ; 6.
; 6. 
7.
 ; 8.
; 8.  ;
; 9.
 ; 10.
; 10.  ;
; 11.
 ; 12.
; 12.  ;
; 13.
 ; 14.
; 14.  ;
; 15.

16.
 .
.
Геометрия 8 класс
-
Прием № 8а. Тема: Окружность.
Тест по теме «Взаимное расположение окружности и прямой»
1.Среди следующих утверждений укажите истинные.
Окружность и прямая имеют две общие точки, если:
а) расстояние от центра окружности до прямой не превосходит радиуса окружности;
б) расстояние от центра окружности до прямой меньше радиуса окружности;
в) расстояние от окружности до прямой меньше радиуса.
2. Закончи фразу, чтобы получилось верное высказывание:
Окружность и прямая имеют одну общую точку, если…
3. Вставьте пропущенные слова.
Окружность и прямая имеют одну общую точку, если … расстояние от … до прямой …
4. Установите истинность или ложность следующих утверждений:
а) прямая а является секущей по отношению к окружности, если она имеет с окружностью общие точки
б) прямая а является секущей по отношению к окружности, если она пересекает окружность в двух точках
в) ) прямая а является секущей по отношению к окружности, если расстояние от центра окружности до данной прямой не больше радиуса
-
Прием № 8. Тема: Вписанная окружность
Тест - 1
-
Центр вписанной в треугольник окружности совпадает с точкой пересечения его …
а) медиан
б) биссектрис
в) серединных перпендикуляров (1 балл) -
Центр вписанной в треугольник окружности равноудален от …
а) сторон
б) углов
в) вершин треугольника (1 балл) -
Центр вписанной в треугольник окружности является точкой пересечения его медиан Этот треугольник
а) прямоугольный
б) равнобедренный
в) равносторонний (1 балл) -
Окружность называется вписанной в многоугольник, если ….
а) все его стороны касаются окружности
б) все его вершины лежат на окружности
в) все его стороны имеют общие точки с окружность (1 балл)
Тест - 2
-
Радиус вписанной в треугольник окружности равен расстоянию от центра окружности до
а) сторон треугольника
б) вершин треугольника
в) углов треугольника (1 балл) -
Центр вписанной в равнобедренный треугольник окружности может лежать …
а) на любой из высот
б) на любой из его медиан
в) на любом из его серединных перпендикуляров (1 балл) -
Центр вписанной в треугольник окружности является точкой пересечения его биссектрис. Этот треугольник может быть …
а) произвольным
б) только равносторонним
в) только прямоугольным (1 балл) -
Многоугольник называется описанным около окружности, если ….
а) окружность имеет общие точки с его сторонами
б) окружность проходит через его вершин
в)окружность является касающейся всех его сторон (1 балл)
-
Тема: Площадь параллелограмма.
Прием № 3. Проверка знаний по теме. Всем даны разные задания по уровням.
1.Постройте параллелограмм, произведите необходимые измерения и вычислите его площадь. (Алеша, Костя, Сережа )
2.Стороны параллелограмма равны 4,2см и 5,6см. Высота, проведенная к большей стороне, равна 3,3см. Вычислите вторую высоту этого параллелограмма.( Полина)
3.Площадь параллелограмма равна 24см. Точка пересечения его диагоналей удалена от прямых, на которых лежат стороны, на 2см и 3см. Вычислите периметр этого параллелограмма. (Антон)
4.Выведите формулу:
1) выражающую площадь ромба (S) через его диагонали m и n.
2) для вычисления площади квадрата (S) по его диагонали . (Ксюша)
5.Вычислите диагонали ромба, если известно, что их длины пропорциональны числам 2 и 3, а площадь ромба равна 12см2. (Маша)
6.Острый угол параллелограмма равен 30, а высоты, проведенные из вершины тупого угла, равны 4см и 3см. Найдите площадь этого параллелограмма. (Коля)
-
Прием № 8. Тема: «Площадь трапеции». Прием № 8
Тест на тему: «Площадь трапеции»
-
Площадь трапеции основания, которой равны a и b, h - высота трапеции, вычисляется по формуле:
А) S = ![]()
Б) S = (a+b)h
В) S =![]()
-
Площадь трапеции равна…
А) произведению суммы оснований на высоту;
Б) произведению полусуммы оснований на высоту;
В) произведению оснований на высоту.
-
В прямоугольной трапеции основания 5см и 7 см, а меньшая боковая сторона
10 см. Найти площадь трапеции:
А) 110 кв.см;
Б) 60 кв.см;
В) 850 кв.см.
-
Параллельные стороны трапеции равны 6 см и 9 см, а ее высота 4 см.
Какова площадь этой трапеции?
А) 216 кв.см;
Б) 60 кв.см;
В) 30 кв.см.
-
Площадь трапеции равна 25 кв.см, а высота трапеции равна 5 см. Найти сумму основании.
А) 250 см;
Б) 10 см;
В) 5 см.
Алгебра 9 класс
-
-
Тема: Графики функций.Прием № 10. Укажи нули функции.
-
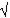
-
-
Прием № 2а Тема: Формула n-го члена арифметической прогрессии.
-
Заполнить пустые клеточки таблицы.
а1
d
n
an
1
8
-6
7
2
-10
2,5
0
3
![]()
5
![]()
4
4
6
23
5
14
0,5
17,5
6
-0,8
4
24
7
4
18
-11
8
![]()
4
![]()
9
-2
1.5
1
10
7
3
18
-
-
Прием №40. Тема: Радианная мера угла.
-
1.Заполни таблицу :
89![]()
-68![]()
91![]()
189![]()
-175![]()
245![]()
Координатная четверть
2."Выключи свет в окнах", т.е. закрась простым карандашом те клетки, где значение выражения равно числу, записанному на портике дома.
1 вариант 2 вариант
Sin 90![]()
Sin 450![]()
Cos 270![]()
Sin 0![]()
Cos 0![]()
tg 0![]()
tg 45![]()
2Cos 60![]()
Cos 360![]()
Cos 90![]()
Sin 180![]()
Cos 270![]()
-
«Проверь и оцени»
Тема «Арифметическая прогрессия»
1. Если а1 = 23, а2 = 11, то d = 12.
2. Если а4 = 5, d = - 2, то а3 = 3.
3. Если а4 = 3,45, d = 0,8, то а5 = 4,25.
4. Если а4 = 29, d = 5, то а1 = 14.
5. Если а1 = 7, d = 2, то а6 = 17.
6. Если а7 = - 4, а9 = - 7, то а8 = 5,5.
7. Если а11 = 450, а1= 10, то d = 44.
8. Если а1 = 6, а2 = 10, то S3 = 30.
-
«Проверь и оцени»
Тема «Степень с рациональным показателем»
1. 23 = 6; 2.
 =
=  ;
; 3. 4 - 1 = - 4; 4.
 = 16;
= 16; 5.
 = 0; 6.
= 0; 6.  = 5;
= 5; 7.
 = 3; 8.
= 3; 8.  =
=  ;
; 9.
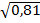 = 2; 10.
= 2; 10. 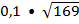 = 16.
= 16.
Геометрия 9 класс
-
-
Прием № 39. Тема: «Нахождение площади, периметра правильного многоугольника, его сторон и радиусов вписанной и описанной окружностей»
-
1.Заполните пустые клетки таблицы для правильного треугольника.
(a3 - сторона правильного треугольника, Р- периметр треугольника, S - площадь треугольника, R - радиус описанной окружности, r - радиус вписанной окружности)
1-3
R
r
a3
P
S
1
√3
2
9
3
2
2.Заполните пустые клетки таблицы для правильного четырехугольника.
(a4 - сторона правильного четырехугольника, Р- периметр четырехугольника, S - площадь четырехугольника, R - радиус описанной окружности, r - радиус вписанной окружности)
2-4
R
r
a4
P
S
1
√2
2
6
3
8
3.Заполните пустые клетки таблицы для правильного шестиугольника.
(a6 - сторона правильного шестиугольника, Р - периметр шестиугольника, S - площадь шестиугольника, R - радиус описанной окружности, r - радиус вписанной окружности)
3-6
R
r
a6
P
S
1
2
2
18
3
√3/2
-
-
Прием № 39. Практическая работа на координатной плоскости по теме: «Движение»
-
Вариант №1
Даны точки в координатной плоскости: А(-1;2); В(4;0); С(-1;-2)
Все задания выполнить на разных координатных плоскостях.
1) Постройте ∆ А1В1С1 относительно начала координат и запишите координаты получившихся точек.
2) Постройте ∆ А22В2С2 относительно оси оу и запишите координаты получившихся точек.
3) Постройте ∆ А3В3С3 выполните поворот на 90° против часовой стрелки и запишите координаты получившихся точек.
4) Постройте ∆ А4В4С4 с помощью параллельного переноса на вектор СК, если К(3;-2) и запишите координаты получившихся точек.
Вариант №2
Даны точки в координатной плоскости: А(3;-2); В(-1;0); С(3;2)
Все задания выполнить на разных координатных плоскостях.
1) Постройте ∆ А1В1С1 относительно начала координат и запишите координаты получившихся точек.
2) Постройте ∆ А2В2С2 относительно оси оу и запишите координаты получившихся точек.
3) Постройте ∆ А3В3С3 выполните поворот на 90° против часовой стрелки и запишите координаты получившихся точек.
4) Постройте ∆ А4В4С4 с помощью параллельного переноса на вектор АК, если К(-1;-2) и запишите координаты получившихся точек.
Матрица дидактического потенциала приемов, форм и видов учебной деятельности ученика
№
Обученность
Обучаемость
Внимание
Память
Модальность
Полушарие
Коммуникативные ОУУН
Организа-ционные ОУУН
Информа-ционные ОУУН
Мыслительные ОУУН
Уровень мотивации
Объем
Объем
Распредел.
Концентр.
Устойчив.
Слов/лог.
Слов./лог.
Нагл/образ.
Эмоцион.
Монологич.
Акт.слушан.
Диалог
Работа в гр.
Планиров.
Самооценка
Раб.мес.тет
Смысл.чтен
Свор.инфор
ТСО
Анализ
Синтез
Сравнение
Логика
Вывод
8
3
I
в
С
8а
4-5
II
в
П
9б
3
I
ва
б
13б
3
I
в
18
3-5
I-III
в
20
3-5
I-III
ва
27
3-5
в
33
3-5
ва
35
3-5
в
39
3-5
ва
40
3-5
в
бп
43
35
в
бп
Приложение № 3.
Урок математики с использованием технологии ИСУД
(изучение новой темы)
Глухова В.В. учитель математики МОУ Боярской СОШ
Особенности детей 6 класса
№
Фамилия, имя
Обученость
Обучаемость
Модальность
Полушарие
Мотивация
Визуальная
Аудиальная
Кинестичес.
Равнополуш..
Правополуш.
Левополуш.
1.
Катя Б.
4
2
+
+
+
Соц.
2.
Витя Г.
4
2
+
+
+
Биол.
3.
Антон К.
3
2
+
+
+
Соц.
4.
Серёжа К.
4
2
+
+
+
Биол.
5.
Саша К.
3
1
+
+
+
Биол.
6.
Святослав С.
3
2
+
+
+
Соц.
Информационная карта урока
(для учителя)
Раздел «Положительные и отрицательные числа»
Тема "Умножение положительных и отрицательных чисел"
Целеполагание для ученика
Целеполагание для учителя
1.Вывести правило умножения положительных и отрицательных чисел;
2.Начать работу по формированию навыка умножения положительных и отрицательных чисел;
3. Развивать вычислительные навыки.
Развитие ОУУ
-
Развивать навык планирования и организации рабочего места
-
Развивать умения сравнивать, выделять главное, обобщать и систематизировать, определять и объяснять понятия.
Предметные цели
-
Работать над вычислительными навыками
-
Формировать знания о правилах умножения положительных и отрицательных чисел и умения применять их в простейших ситуациях
-
Обогащать словарный запас
-
Проверить полноту, глубину и прочность изученных знаний, умений и навыков по сложению и вычитанию положительных и отрицательных чисел
-
Воспитывать ответственное отношение к учебному труду.
Опорные понятия
Новые понятия, термины
Сложение, вычитание, умножение положительных и отрицательных чисел
Правила умножения чисел с разными знаками, отрицательных чисел.
Домашнее задание: №
Этапы урока, формы, краткое содержание
Дидактическое оснащение
Деятельность учителя, рефлексия
1.Орг. момент
Настрой на урок
Презентация ,
стих
Показ презентации
2.История отрицательных чисел.
Рассказ учащегося.
Презентация.
Показ презентации, дополнительный материал.
3.Разминка.
Задания в презентации
Карточки .
Карточки по уровням обучаемости, устные ответы.
4.Новая тема.
Решение примеров на доске. Презентация.Карточки.
Работа с доской.
5. Физминутка.
Презентация. Зарядка для глаз.
6. Первичное закрепление знаний.
Карточки .
Карточки по уровням обучаемости.
7. Вторичное закрепление знаний.
Задание в презентации.
Показ презентации
8. Домашнее задание
На доске.
Устное разъяснение.
9. Итог урока.
Презентация.
Рефлексия.
План-конспект урока.
Этапы урока
Ход урока
Дифференциация, индивидуальная работа учащихся
1.Орг. момент
Постановка цели и мотивационной деятельности
Настрой на урок. (Слайд 1.)
Очень восхитительные
Числа положительные!
А числа отрицательные?
Тоже замечательные!
Только ноль, как постовой,
Охраняет их покой.
Если точка вам нужна -
Выходите вы с нуля.
Ну а противоположные
Вообще не очень сложные!
2. История отрицательных чисел
3. Разминка
В Древнем Китае были известны лишь правила сложения и вычитания положительных и отрицательных чисел; правила умножения и деления не применялись
В Индии относились к отрицательным числам с некоторым недоверием, считая их своеобразными, не совсем реальными. Бхасхара прямо писал: «Люди не одобряют отвлеченных отрицательных чисел»… (Слайд 2.)
-
Найдите значение выражения. (Слайд 3).
Если х=-3, то -х=
Если -а=8,5, то а=
Если -(-в)=7, то -в=
2. Составьте верные равенства
-(-а)= 60=
-(-0,4)= 7,23=
- =-4
3. Замените одним словом: (Слайд 4.)
-
Числа слева от нуля.
-
Числа больше нуля.
-
Этот знак пишут перед числами, которые меньше нуля.
-
Все натуральные числа, им противоположные и ноль.
-
Числа 2 и ( -2).
-
Синоним «модуля».
-
Таким числом обозначается понижение величины.
-
Таким числом обозначается повышение величины.
-
Индивидуальные задания:
Приложение №1.
-
Решить примеры
-
Разделить примеры на 4 группы
-
Записать свои примеры по образцу.
Слайд 5.
Сообщение ученика.
Прием № 74
Прием № 20
Прием № 23.
Прием № 24.
Прием № 17
4.Новая тема
( Слайд 6) - Мы учились складывать , вычитать положительные и отрицательные числа, чему ещё осталось научиться? Вот сегодня и будем учиться умножать положительные и отрицательные числа.
На доске записаны примеры на умножение разные случаи:
-8* 2 = -16 5 * (-7) = -35 -4 * (-8) = 32
- Какой можно сделать вывод?
Вывод: 1. Произведение положительного и отрицательного числа есть число отрицательное.
2.Произведение двух отрицательных чисел есть число положительное. (Слайд 7 )
Приём № 1 (активное слушание с опорой на визуальный ряд)
5.Физминутка
Немного отдохнем. (Слайд 8)
6. Первичное закрепление знаний.
- Сейчас мы применим правило на практике. Запишите результаты: Приложение № 2.
(Слайд 9.)
1 группа:- 8 * (-4) = - 9 * 5=
- 6 * 6 = - 4 * 5 =
- 2 * (-7) = 10 * (-3) =
-1 * (-1) = - 1* 1 =
2 группа: Задание. Выполните вычисления. К каждому получившемуся числу найдите противоположное число в таблице, соотнесите его с буквой из таблицы и запишите эту букву.
- 8 * (-4) = - 9 * 5=
- 6 * 6 = - 4 * 5 =
- 2 * (-7) = 10 * (-3) =
-1 * (-1) = - 1* 1 =
30
-14
-1
0
36
20
-32
1
45
ж
м
н
н
е
и
у
е
о
ответ:
Саше, Антону, Святославу.
Кате, Вите, Сереже
Прием № 33.
7. Вторичное закрепление знаний.
Приложение № 3. Задание. А) Отметьте галочкой ( ) те клетки таблицы, в которых будут получаться отрицательные произведения.
Б) Запишите «0» в тех клетках таблицы, в которых произведение будет равно нулю;
В) Поставьте знак «?» в тех клетках таблицы, в которых вы не можете подсчитать ответ;
Г) Произведение какой пары чисел из таблицы будет наименьшей? Заполните соответствующую клетку таблицы этим ответом.
*
-1
-2
-3
-4
0
1
2
3
4
-1
-2
-3
Саше, Антону.
Прием № 39.
Вите, Кате, Серёже, Святославу.
8. Закрепление знаний.
Приложение № 4. Установи соответствие: учащиеся должны найти в правой и левой части таблицы примеры с одинаковыми результатами и записать их номера через тире. (Фото деревьев)
1) - 4,2 * ( - 5) секвойя
2) - 2 * ( - 7,8)эвкалипт
3) 12 * ( - 5,8)трав. ива
4) -1,3 * 2,4 бонсай
5)9 * ( - 9) тис
1) -3 * 27
2)0,39 * (-8)
3)-2,6 *6
4)-3 * ( - 7)
5) - 6* 11,6
Самым маленьким деревом на планете является травянистая ива произрастающая в основном в арктической тундре. 6-сантиметровая карликовая ива
Наибольшей высоты достигают деревья вида секвойя - до 113 м, эвкалипт
Бонса́й - искусство выращивания точной копии настоящего дерева в миниатюре. Слово «бонсай» происходит от китайского «пэнь-цай». Возникло искусство в 231 году до н. э. в Китае. (Слайд 10.)
Прием № 58.
9. Домашнее задание
номера по учебнику
10. Итог урока.
Я могу ответить на вопрос… (Слайд 11.)
-
- Какое действие с положительными и отрицательными числами мы рассматривали на уроке?
-
- Как прочитать запись 2,5*(-7)?
-
- Как перемножить два числа с разными знаками?
-
- Привести пример на умножение двух чисел с разными знаками и решить его.
-
- Как перемножить два числа с одинаковыми знаками?
-
- Привести пример на умножение двух чисел с одинаковыми знаками и решить его.
Спасибо за урок. Вы сегодня молодцы.
(Слайд 12.)
Приложение к уроку №1.
-
Реши примеры:
- 20 + 71 =
-17,9 + 20 =
- 2,46 + 12 =
- 17 + 23,6 =
-7 - 12 =
- 8 - 16 =
- 6,4- 6,25 =
-1,8 - 1,14 =
3,4 + 8,9 =
5,77 + 2,9 =
7,99 + 4,1 =
7,8 + 4,08 =
7 - 12 =
-
- 15,8 =
18 - 23,34 =
1,3 - 8 =
-
2. Распредели примеры на 4 группы и реши:
-7 - 12 = - 20 + 71 =
3,4 + 8,9 = 5,77 + 2,9 =
7,99 + 4,1 = 7,8 + 4,08 =
-17,9 + 20 = 7 - 12 =
-
- 15,8 = 18 - 23,34 =
1,3 - 8 = - 2,46 + 12 =
- 17 + 23,6 = - 8 - 16 =
- 6,4- 6,25 = -1,8 - 1,14 =
3.Допиши 3 примера по образцу и реши:
-7 - 12 =
- 20 + 71 =
7 - 12 =
3,4 + 8,9 =
№ 2.
1 уровень
Реши примеры:
- 8 * (-4) = - 9 * 5=
- 6 * 6 = - 4 * 5 =
- 2 * (-7) = 10 * (-3) =
-1 * (-1) = - 1* 1 =
2 уровень
Задание. Выполните вычисления. К каждому получившемуся числу найдите противоположное число в таблице, соотнесите его с буквой из таблицы и запишите эту букву.
- 8 * (-4) = - 9 * 5= - 6 * 6 = - 4 * 5 =
- 2 * (-7) = 10 * (-3) = -1 * (-1) = - 1* 1 =
- 8* 0 =
30
-14
-1
0
36
20
-32
1
45
ж
м
н
н
е
и
у
е
о
Ответ:
№ 3.
1 уровень
Задание. А) Отметьте галочкой ( ) те клетки таблицы, в которых будут получаться отрицательные произведения:
*
- 4
- 3
- 2
- 1
0
1
2
3
4
- 3
- 2
- 1
2 уровень
Задание. А) Отметьте галочкой ( ) те клетки таблицы, в которых будут получаться отрицательные произведения:
*
- 4
- 3
- 2
- 1
0
1
2
3
4
- 3
- 2
- 1
Б) Запишите «0» в тех клетках таблицы, в которых произведение будет равно нулю;
В) Поставьте знак «?» в тех клетках таблицы, в которых вы не можете подсчитать ответ;
Г) Произведение какой пары чисел из таблицы будет наименьшей? Заполните соответствующую клетку таблицы этим ответом.
№ 4.
-
Эвкалипт
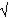
Травянистая ива
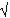
Бонсай
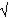
Секвойя
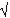
Тис
Презентация
Приложение № 4.
Индивидуальная программа развития ученика 5 класса
Глухова Виктора
Параметры учебного успеха уровень которых недостаточный.
Этап актуализации знаний
Этап закрепления знаний
Планирование
№5 - сравни два числа и запиши ответы на вопросы о них.
№7 - задания по нумерации.
№8 - найди лишнее выражение.
№5 - соедини решение задачи с выражением.
№12 - реши примеры и проверь по эталону.
№13 - реши и прочитай слово.
Распределение внимания
№1 - 14
№2 - распредели примеры на две группы по ответам
№3 - сгруппируй величины
№6 - изучи закономерности
№12 - распредели величины в порядке возрастания
№7 - реши и прочитай слово
№9 - магические квадраты
Словесно-логическая память
№1 - 8
№9 - установи закономерности и заполни пустые клетки
№10 - вставь пропущенные числа, чтобы получилась верная запись
№10 - придумай вопрос к задаче и реши её
Монологическая речь
№4 - охарактеризуй число как можно полно
№6
№8 - найди лишнее выражение и объясни, почему оно лишнее, остальные реши
№10
№15 - реши задачу, используя план решения
Диалог
-
№10
Работа в группе
310
№12 - расположи величины в порядке возрастания
№5,7
№8 - заполни таблицу, пользуясь формулами
Смысловое чтение
№5,
№11 - распредели меры по величинам
№5, 10
Сворачивание информации
№1 - 14
№13 - вставь пропущенные числа
№14 - сравни две таблицы, выпиши из правой буквы, соответствующие числам и прочитай слово
№1 - 15
№15 - реши задачу, используя план решения
Параметры учебного успеха уровень которых достаточный
Этап объяснения нового материала
Этап диагностики знаний
Объём внимания
№1 - придумай задачу по выражению
№2 - продолжи вычисления
№3 - реши задачу и придумай обратную
№1 - математический диктант
№2 - тестовое задание
№4 - верно, не верно
№5 - блиц -турнир
Концентрация внимания
№1 - 8
№5 - сравни два числа и запиши ответы на вопросы о них
№6 - выполни вычисления и сравни результаты
№5
№6 - заполни таблицу
Устойчивость внимания
№7 - сравни два способа и выбери удобный
№8 - составь план решения и запиши его
№7 - найди и исправь ошибки
№8 - заполни таблицу, пользуясь формулами
Наглядно-образная память
№1-7
№8,
№10 - прочитай схему и реши задачу
Активное слушание
-
№5а - запиши буквенное выражение и реши задачу
№9 - цифровой диктант
Самооценка
№1а - придумай задачу по выражению
№2,8
№4 - охарактеризуй число как можно более полно
№4,5 - 11
№11 - тестовые задания по выбору правильного ответа
Анализ
№1 - 8
№1 - 11
№3 - собери из карточек схему-алгоритм
Синтез
№1 - 8
№1 - 11
Логика
№3 - 5
№5, 8, 10.11
№6а - подумай, как заполнена таблица и заполни пустые клеточки
Данные по контрольной работе № 4 от 30.10.08
№
Ф.И. ученика
№ задания
Уровень
1
2
3
4
1.
Базуева Катя
1
1
1
1
3
2.
Глухов Витя
1
0
1
1
2
3.
Котельников Саша
1
1
0
0
1
4.
Костенков Антон
*
0
0
0
0
5.
Кузьминых Серёжа
1
1
1
1
3
6.
Сибриков Святослав
*
0
0
0
0
Уровни знаний
0
1
2
3
*
-
П
Кол-во человек
2
4
3
2
-
-
2-е зад.
Результат %
33
67
50
33
-
-
Приложение 5.
Матрица параметров учебного успеха учеников 7 класса 2009-10 учебный год
№
Обученность
Обучаемость
Внимание
Память
Модаль-ность
Полушарие
Коммуникат.
ОУУН
Организац.
ОУУН
Информац.
ОУУН
Мыслительные
ОУУН
Уровень мотивации
Объём
Распределение
Концентрация
Устойчивость
Слов.-логическая
Наглядно-образная
Эмоциональная
Визуальная
Аудиальная
Кинестетическая
Равнополушарное
Левополушарное
Правополушарное
Монолог. речь
Активное слушание
Диалог
Работа в группе
Планирование
Рабоч. место, оформ.
Самооценка
Смыслов. чтение
Сворач. информации
Разворач. информации
ТСО, медиатехн.
Анализ
Синтез
Сравнение
Логика
Вывод
4
с
2
2
2
3
3
3
1
1
1
1
1
б
4
с
2
2
с
4
1
2
3
3
3
3
1
1
1
1
б
2
3
3
1
1
1
1
с
2
3
Матрица параметров учебного успеха учеников 8 класса 2008-09 учебный год
№
Обученность
Обучаемость
Внимание
Память
Модаль-ность
Полушарие
Коммуникат.
ОУУН
Организац.
ОУУН
Информац.
ОУУН
Мыслительные
ОУУН
Уровень мотивации
Объём
Распределение
Концентрация
Устойчивость
Слов.-логическая
Наглядно-образная
Эмоциональная
Визуальная
Аудиальная
Кинестетическая
Равнополушарное
Левополушарное
Правополушарное
Монолог. речь
Активное слушание
Диалог
Работа в группе
Планирование
Рабоч. место, оформ.
Самооценка
Смыслов. чтение
Сворач. информации
Разворач. информации
ТСО, медиатехн.
Анализ
Синтез
Сравнение
Логика
Вывод
4
с
2
2
2
3
3
3
1
1
1
1
1
б
4
с
2
2
3
3
3
с
4
1
2
3
3
3
3
3
1
1
1
1
б
2
3
3
1
1
1
1
с
2
Матрица параметров учебного успеха учеников 9 класса 2007-08 учебный год
№
Обученность
Обучаемость
Внимание
Память
Модаль-ность
Полушарие
Коммуникат.
ОУУН
Организац.
ОУУН
Информац.
ОУУН
Мыслительные
ОУУН
Уровень мотивации
Объём
Распределение
Концентрация
Устойчивость
Слов.-логическая
Наглядно-образная
Эмоциональная
Визуальная
Аудиальная
Кинестетическая
Равнополушарное
Левополушарное
Правополушарное
Монолог. речь
Активное слушание
Диалог
Работа в группе
Планирование
Рабоч. место, оформ.
Самооценка
Смыслов. чтение
Сворач. информации
Разворач. информации
ТСО, медиатехн.
Анализ
Синтез
Сравнение
Логика
Вывод
4
с
2
2
2
3
3
3
3
1
1
1
1
1
б
3
4
с
2
2
3
3
3
3
с
4
1
2
3
3
3
3
3
1
1
1
б
1,5
2
3
3
1
1
1
1
с
2
3
Приложение № 6.
Определение уровня обучаемости
2007 год. 7 класс. Алгебра. Тема: Линейное уравнение. сентябрь
-
Напишите, что вы узнали нового на уроке.
-
Линейное уравнение - это…
-
Решите уравнение по образцу:
2х +9 = 13 + х 4у +15 = 6у +17
2х - х = 13 - 9
х = 4
2· 4 + 9 = 13 = 4
-
Восстановите уравнение:
3х = 5х =
х = х =
-
Вырази каждую из букв, входящих в формулу через остальные
v · t = S L · R = U m · z = P
-
№
Фамилия, имя учащегося
Уровень
сентябрь
апрель
1.
2.
3.
4.
5.
6.
Котельникова Ксения
Драчев Максим
Котов Артем
Новокрещенов Иван
Калабина Таьяна
Самарин Николай
1
2
2
1
2
1
1
3
2
1
2
1
Сентябрь Апрель
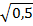
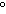
2008-2009 уч. г. Алгебра 8 класс (апрель)
-
Напишите, что Вы узнали нового на уроке.
-
Запишите свойства степени с целым показателем.
-
Найдите значение выражения:
а)3-4 * 37 б) 24 : 2-2
и) (-4-2) -3 в) 5-14 * 517
4. Представьте выражение в виде степени с основанием 5 и найдите его значение:
а) 125 * 5-4 б) 55: 625
5. Упростите выражение:
2ав3 * 2а-3в-6
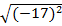
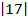
2009-10 уч. год Алгебра 9 класс (октябрь)
-
Напишите, что Вы узнали нового на уроке.
-
На примере неравенства (х - 5)(х + 7)(х + 9) < 0 запишите, как решают неравенства методом интервалов.
-
Решите неравенство, используя метод интервалов: (х + 7)(х - 4) > 0
-
Решите неравенство: (х - 2)(х + 5)(х + 12) > 0
-
Найдите, при каких значениях произведение (х+ 48)(х - 37) (х - 42) положительно.
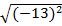
Уровень обучаемости по алгебре 9 класс (апрель)
-
Напишите, что Вы узнали нового на уроке.
-
Выразите в градусах 4,5 рад; 0,2 рад.
-
Найдите радианную меру угла, равного: 1350, - 1200, 3000, - 2250
-
Вычислите: 2
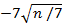 +
+ 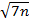
-
Найдите значение выражения: 2
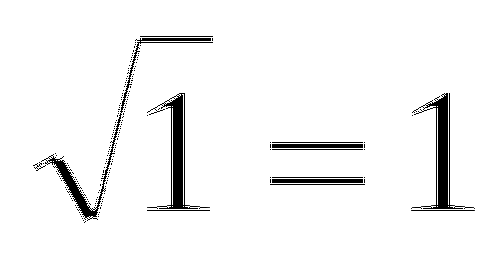 -
- 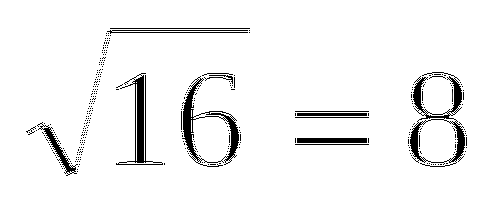
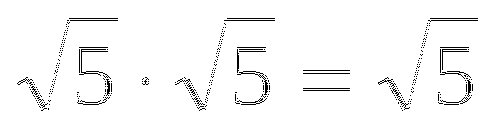
Приложение №7.
Определение уровня владения учащимися общеучебных мыслительных навыков по алгебре
8 класс (сентябрь).
Ф.И. учащегося
анализ
синтез
сравнен.
логика
вывод
уровень
Драчев М.
3
3
2
1
3
2
Котельникова К.
1
2
2
1
2
1
Калабина Т.
2
3
1
1
3
2
Котов А.
3
3
3
3
3
3
Новокрещенов В.
2
3
3
1
2
2
Самарин К.
2
1
1
1
1
1
-
Анализ
Из рациональных выражений
3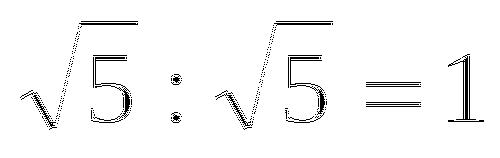

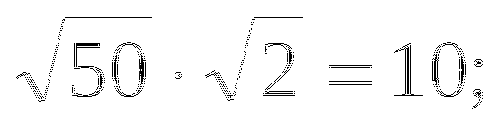 а2в, (х - у)2 - 4ху, m - 5 8 а2 - 2ав
а2в, (х - у)2 - 4ху, m - 5 8 а2 - 2ав
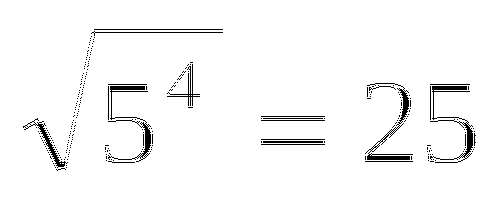 2 m + 5, х2+у2,12,
2 m + 5, х2+у2,12,
(д + 4)2 + с, а +7 (х - у )(х2 + у2)
 3
3
а) целыми выражениями;
б)дробными выражениями.
Чем они отличаются?
-
Синтез
Равенство, верное при всех допустимых значениях входящих в него переменных, называется …
-
Сравнение
Не выполняя вычислений, расположите дроби в порядке возрастания их значений:
5 : 6; 5 . 0,1 5 . (-7)
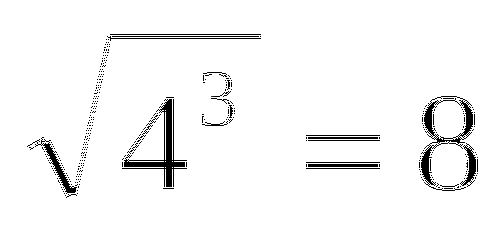
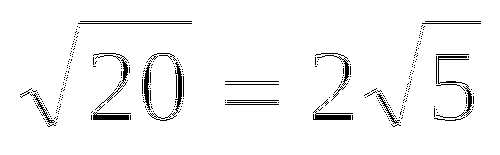
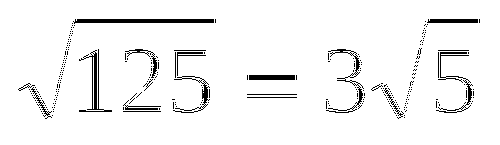 16 16 16
16 16 16
-
Логика (причинно-следственные связи)
Сократите дробь
2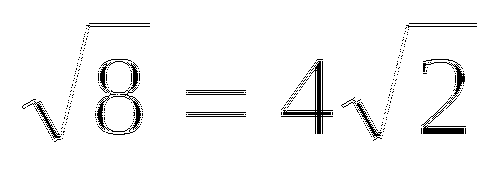
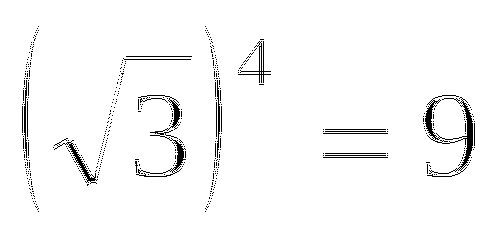 m+ 14 = = 2
m+ 14 = = 2
m 2 - 49 m - 7
p 2 - 25q2 = q+5q
2 - 25q2 = q+5q
2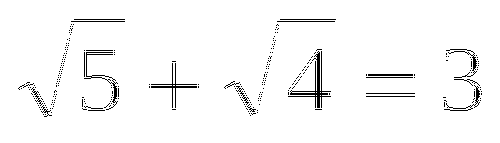 p- 10q 2
p- 10q 2
-
Вывод
Как выполняют сложение и вычитание дробей с разными знаменателями?
9 класс (октябрь)
Ф. И. ученика
Анализ
Синтез
Сравнение
Логика
Вывод
Уровень
Драчев М.
3
2
2
3
3
3
Калабина Т.
3
2
2
3
2
2
Котельникова К.
3
1
1
1
1
1
Котов А.
3
3
2
3
3
3
Новокрещенов В
3
2
1
2
1
2
Самрин Н.
3
1
1
2
1
1
-
Анализ:
Н а рисунке изображен график. Выберите соответствующую формулу этого графика:
а рисунке изображен график. Выберите соответствующую формулу этого графика:
а) ![]()


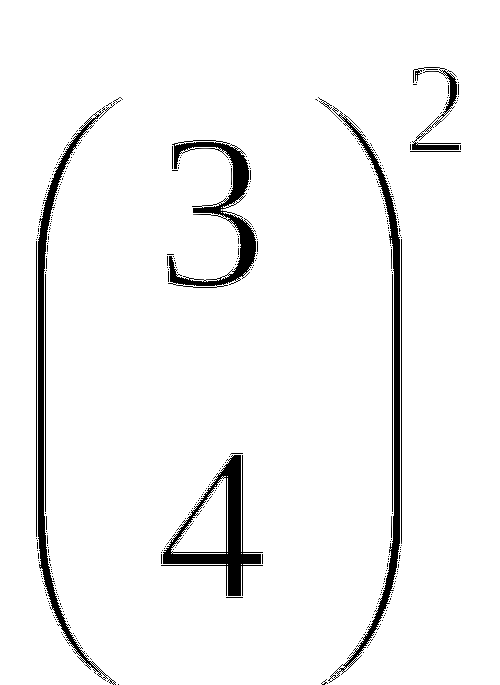
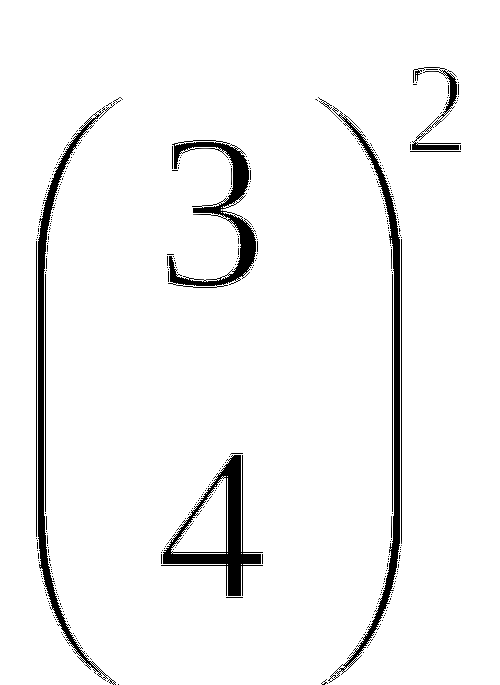
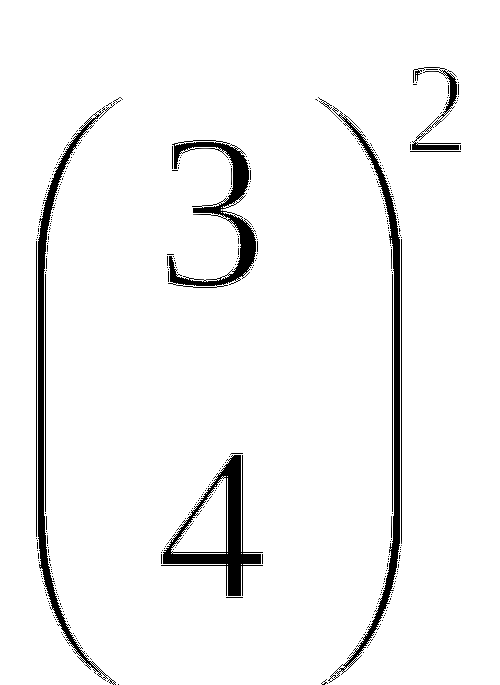
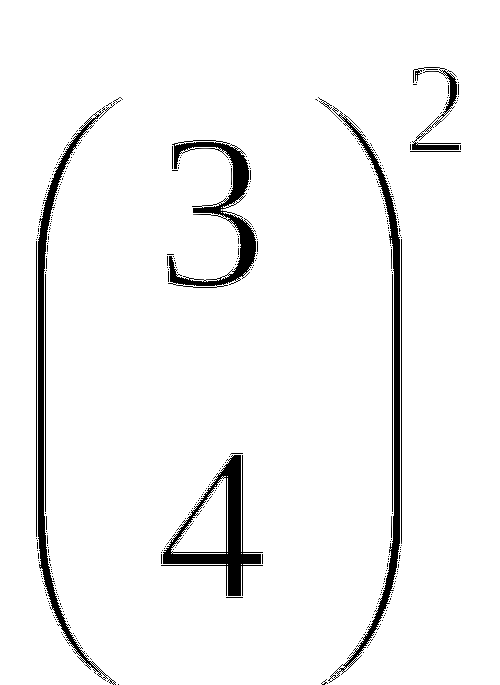 б)
б) ![]() 4
4
в) ![]()
г) ![]()
2. Синтез:
у = ах2 + вх + с - это…
3.Сравнение
В чем сходство и различие функций: у = ах2 при а > 0, у = ах2 при а < 0
-
Выберите для каждого предложения нужную формулу.
-
Параллельный перенос вдоль оси у вниз а) у =
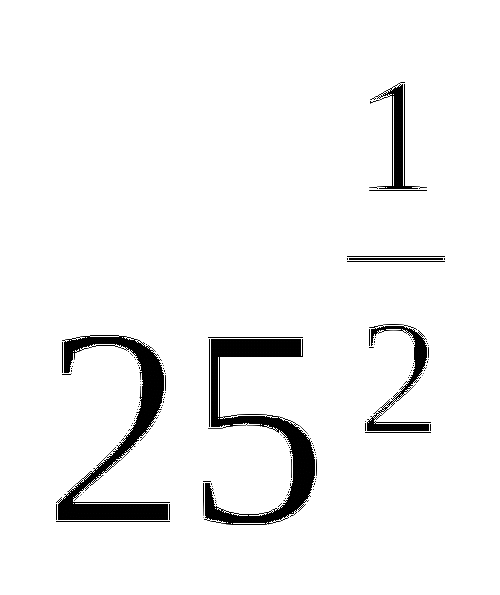 (х - 5)2
(х - 5)2 -
Параллельный перенос вдоль оси х вправо б) у =
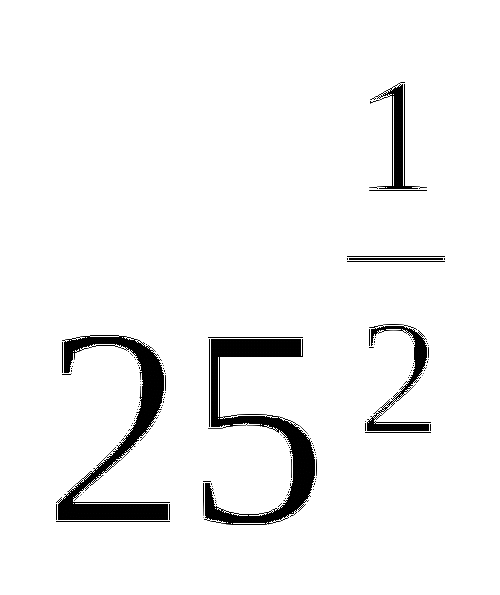 х2 + 3
х2 + 3 -
Параллельный перенос вдоль осей х и у в) у =
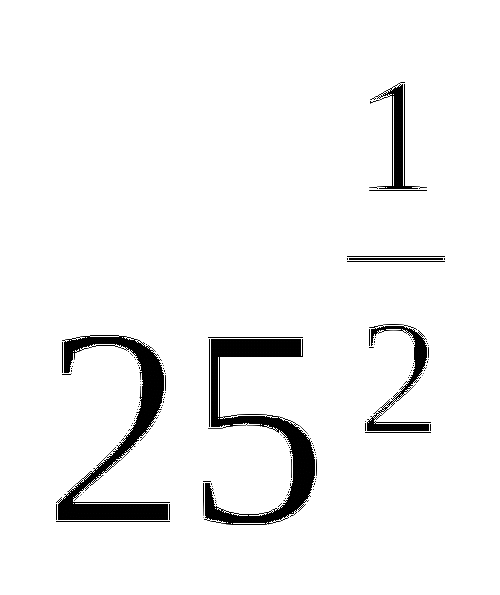 (х - 3)2 + 2
(х - 3)2 + 2 -
Параллельный перенос вдоль оси у вверх г) у =
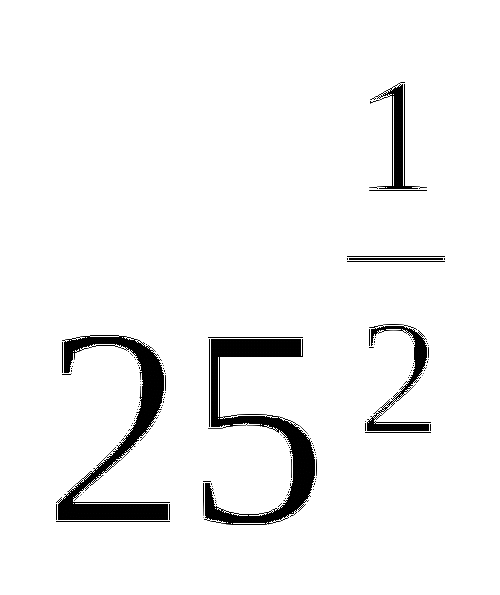 (х + 5)2
(х + 5)2 -
Параллельный перенос вдоль оси х влево д) у =
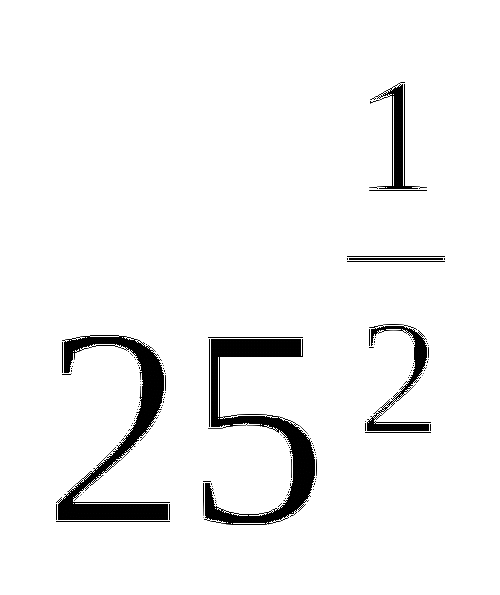 х2 - 3
х2 - 3
-
Как построить график квадратичной функции?