Рабочая тетрадь к спецкурсу 'Живая геометрия' для 6 класса

Автор: Тятюшкина А.А.- учитель математики МОУ «СОШ №11»

Рецензент:

Чумакова Н.А., зам. дир. по УР МОУ «СОШ №11» г. Братска

Живая геометрия 6 класс. Задания для обучения и развития учащихся. - МОУ«СОШ №11», 2009. - 29 с.

Предлагаемое пособие создано для работы на уроках геометрии с учащимися 6 класса и ориентировано на развитие мышления и творческих способностей.

В данное пособие вошли тесты, практические, самостоятельные и контрольные работы.

У ч е б н о е п о с о б и е

Тятюшкина А.А.

ЖИВАЯ ГЕОМЕТРИЯ

6 класс

Задания для обучения и развития учащихся

Редактор Чумакова Н.А.

Компьютерная вёрстка Серёгина А.С.

© МОУ «СОШ №11»

© Тятюшкина А.А.

Содержание

1. Введение

2

2. Тема: Точка. Линия. Плоские и пространственные фигуры

3

3. Тема: Отрезок. Луч. Прямая.

5

4. Треугольники. Виды треугольников.

7

5. Круг и окружность. Их элементы.

9

6. Обобщение изученного материала по теме: «Отрезки. Конструкции из отрезков».

11

7. Тема: Отрезки. Конструкции из отрезков.

13

8. Тема: Сравнение углов. Построение угла, равного данному.

15

9. Тема: Площадь прямоугольника и площадь треугольника.

17

10. Тема: Измерение углов. Транспортир.

19

11. Тема: Получение фигур из параллельных отрезков.

21

12. Тема: Расстояние между точками, от точки до фигуры, прямой и плоскости.

23

13. Координаты точек. Построение точек в системе координат.

25

14. Тема: Построение фигур в системе координат.

27

В

29

29ведение

Предлагаемое пособие создано для работы на уроках геометрии с учащимися 6 класса и ориентировано на развитие мышления и творческих способностей. Рабочая тетрадь является дополнением пропедевтического курса «Живая геометрия» 6 класс, адаптированная программа, утверждена ГИМНЦ г.Братска, 2009 г.

Пособие хорошо приспособлено для организации учебной деятельности и для самостоятельной работы учащихся.

Основными достоинствами данного пособия являются: учет индивидуальных способностей учащихся; проверка качества усвоения не только практического, но и теоретического учебного материала; возможность детальной проверки каждой темы курса; осуществление оперативной диагностики результата овладения учебным материалом каждым учеником; экономии учебного времени при проверке знаний и оценке результатов обученности; оживление процесса обучения.

Главной отличительной особенностью пособия является то, что большинство заданий имеет занимательную форму.

Наряду с формированием математических знаний, задания рабочей тетради помогают развивать у учащихся логическое мышление, интерес к предмету.

Занимательная форма многих заданий привлекает учащихся, побуждает их к четкой, последовательной и аккуратной деятельности.

Т

2ЕМА: Точка. Линия. Плоские и пространственные фигуры.

Самостоятельная работа.

1. Отметить две точки P и Q и нарисует кривую линию с началом в точке Р и проходящую через точку Q. Сколько таких линий ты можешь нарисовать?

2. Выпиши точки, через которые проходит линия на рисунке.

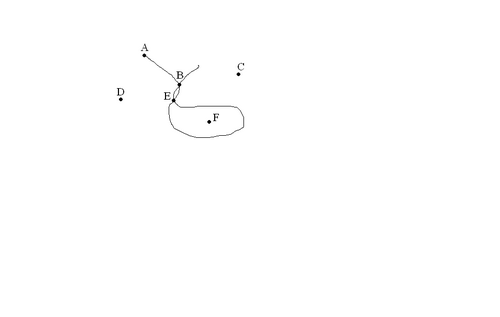
3. Нарисуй трехзвенную ломаную. Назови ее и выпиши названия всех звеньев.

4. Даны точки. Нарисуй разными карандашами две замкнутые ломаные с вершинами в данных точках. Выпиши названия этих ломаных линий.

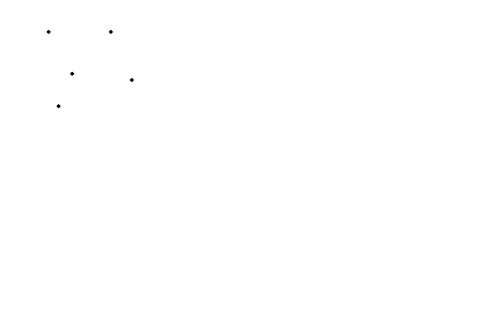
О

3тгадайте, кто это ходит в костяном пальто? Догадались кто это? А теперь постройте систему координат и отметьте точки.

(10;0), (-8;2), (-8;4), (-6;6), (-4;6), (-2;4), (-2;2), (0;4), (2,5;4), (3;2), (1,5;2), (3;2), (0;0), (1;-1), (-9;-1), (-10;0) и (1;3).

ЭКОсправочник: Черепахи - это древние существа, на Земле появились много миллионов лет назад. Большинство их ровесников давно исчезли с лица земли. Черепахи пока сохранились. Пока! Особенно досадно то, что кроме человека, никто не угрожает черепахе. Несчастье морских черепах в том, что они съедобны. Самая большая - морская кожистая черепаха. Её панцирь достигает 2-х метров, а вес - 600 кг. Из сухопутных самая крупная - слоновая черепаха. Эти животные фантастически живучи : до 10 часов остаются живыми в атмосфере, начисто лишенной кислорода. Зеленая, или суповая, черепаха (длиной до 1,5 м и до 400 кг весом) - примерный вегетарианец: кормится морскими водорослями.

В настоящее время в Южной и Северной Америке насчитывается около 100 заповедников по охране и разведению черепахи.

Т

28ЕМА: Построение фигур в системе координат.

Графический диктант.

1. Отгадай и построй:

З

Что за чудо! Вот так чудо!

Сверху блюдо, снизу блюдо!

Ходит чудо по дороге,

Голова торчит и ноги.

агадка:

5

27) Какие из данных фигур являются плоскими, а какие пространственными?

Т

4ЕМА: Отрезок. Луч. Прямая.

Самостоятельная работа.

1. На сколько отрезков разбит отрезок PQ точками А и D. Выпиши названия всех получившихся отрезков.

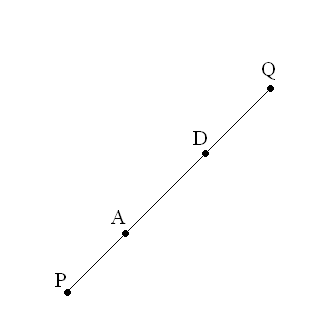
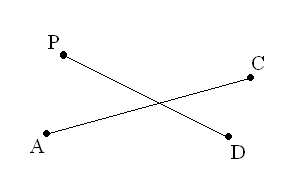
2) С помощью циркуля сравни два отрезка на рисунке.

3. Отметь точки А, В, С. Начерти лучи АВ, ВС, СА.

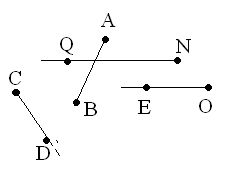
4. Назови все лучи, изображенные на рисунке. Какие из них пересекают отрезок АВ.

5

5) Построй на координатной плоскости четырехугольник ABCD, если А (-10;-2); В (-2;2); С (-2;-6); D (-10;-6). Найди периметр и площадь этого четырехугольника. Проведи диагонали и найди координаты точки пересечения этих диагоналей.

6. Даны точки:

А (0;4), В (-3,5;2), С (7,2;-7,2), D (3;10), Е (-1;-2), F (5;0)

а) Выбери точки, которые расположены выше оси абсцисс.

б) Выбери точки, которые лежат на оси ординат.

в) Выбери точки, которые расположены на оси абсцисс.

Т

26ЕМА: Координаты точек. Построение точек в системе координат.

Самостоятельная работа.

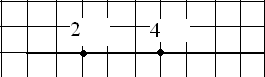
1. Определите начало, направление и шаг координатной прямой.

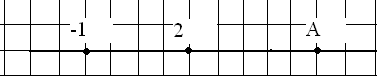
2. Определи координату точки А.

3. Построй треугольник ОВС в системе координат, если О (0;0); В (4;6); С (1;5).

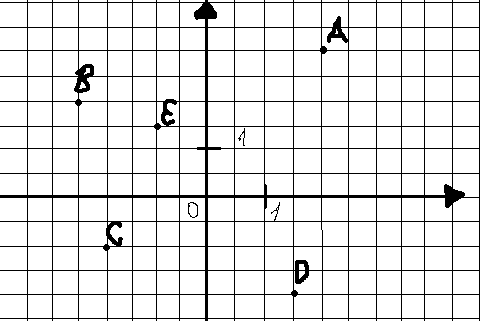
4. Найди координаты точек A, B, C, D, E.

3. 5

   25) Отметь в тетради точки О и К. Проведи через них прямую. Назови все получившиеся фигуры.

3. Проанализируй чертеж и укажи равные отрезки:

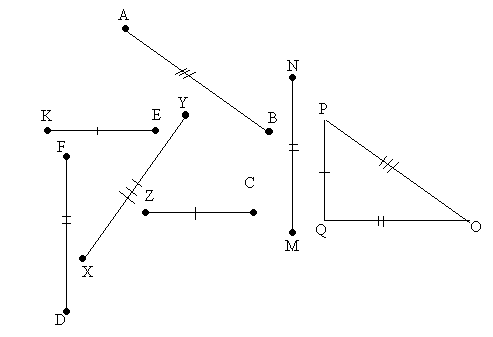
3. Проанализируй чертеж и данные к задаче. Найди длины указанных отрезков. АВ = 8 см, АС = 15 мм. CD - ?

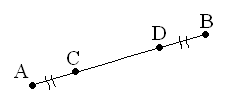
3. На отрезке АВ поставили точки C и D так, что АС = 17 см, а расстояние от точки D до точки В в три раза больше, чем, расстояние от точки С до точки D. Найдите длину отрезка BD, если отрезок АВ = 29 см.

Т

6ЕМА: Треугольник. Виды треугольников.

Практическая работа.

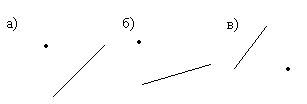
1. Если эти точки соединить отрезками, то они станут вершинами треугольника. Соедини их отрезками. Какой треугольник получится?

а)

б)

в)

2. Найди среди этих треугольников все остроугольные, тупоугольные и прямоугольные.

1

3

9

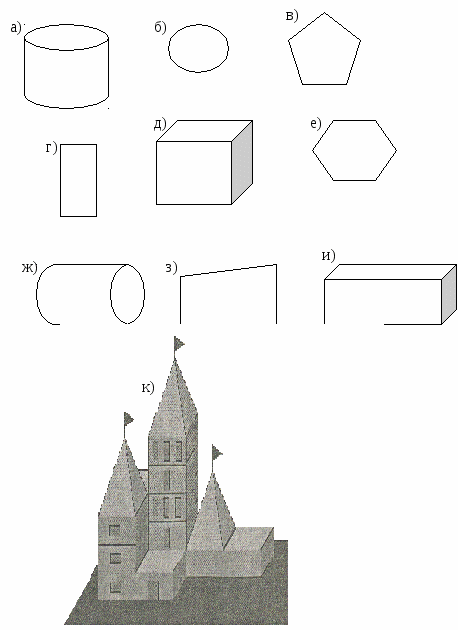
6

2

7

3) а) В этом треугольнике две стороны одинаковой длины. Покажи их. Треугольники с двумя одинаковыми сторонами называются равнобедренными.

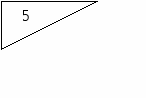
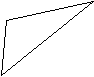
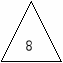
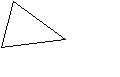
б) Вот еще несколько равнобедренных треугольников. Покажи в каждом из них одинаковые стороны.

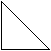
5

7) Покажи на рисунке расстояние от точки А до прямой а.

6)Назови взаимное расположение прямой и плоскости.

Покажи на рисунках, как может располагаться прямая по отношению к плоскости.

Т

24ЕМА: Расстояние между точками, от точки до фигуры, прямой и плоскости.

Самостоятельная работа.

1. Построй 3 точки, не лежащие на одной прямой. Соедини попарно их отрезками. Измерь длины получившихся отрезков.

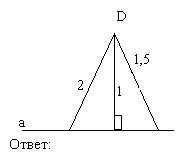
2. Чему равно расстояние от точки D до прямой а.

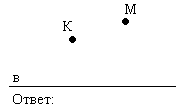
3. Определи (измерением) расстояния от точек К и М до прямой в.

4. Покажи на рисунке расстояние от точки до лягушки.

в

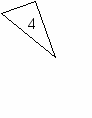
23) Есть ли среди этих треугольников равнобедренные….

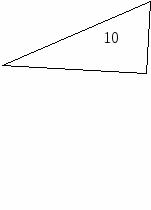
г) Попробуй построить два равнобедренных треугольника

4) А в этом треугольнике все стороны одинаковой длины. Такой треугольник называется равносторонним.

А

4

5теперь попробуй найти равносторонние треугольники среди множества других.

1

3

2

6

5. П

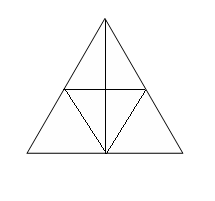
   в)осчитай сколько треугольников изображено на рисунке?

а)

б)

Т

8ЕМА: Круг и окружность. Их элементы.

Тест.

1. Вот три круга: жёлтый, красный и голубой. Скажи у какого из них радиус больше.

а) у жёлтого; б) у красного; в) у голубого

2. Дан круг. Измерь радиус круга.

а) 1 см; б) 2 см 3мм; в) 1 см 5 мм.

3. Сколько общих точек имеют две окружности с радиусами 2 см и 4 см, если расстояние между их центрами равно 3 см.

а) одну; б) две; в) не имеют общих точек.

4. Какую фигуру образуют все точки плоскости, которые удалены от данной окружности на одно и то же расстояние больше или равное радиусу этой окружности?

а) точку; б) прямую; в) плоскость.

п

9олучилась? А теперь выполни аналогичное задание, построив тупоугольный равнобедренный треугольник.

\

4) Построй произвольный четырехугольник, проведи в нем все диагонали. Через каждую вершину проведи прямую, параллельную данной диагонали. Какая фигура получилась?

Т

22ЕМА: Получение фигур из параллельных отрезков.

Практическая работа.

1. Построй какой - нибудь четырехугольник, в котором есть параллельные стороны.

2. Построй куб ABCDA₁B₂C₃D₄, укажи:

а) все отрезки, которые параллельны грани основания грани;

б) все прямые, которые скрещиваются с прямой АВ.

3. Начерти правильный треугольник, через каждую вершину этого треугольника проведи прямую, параллельную противоположной стороне. Какая фигура

5

21) У какого колеса диаметр больше, если первый на расстоянии в 380 м. сделал 150 оборотов, а второй на этом же расстоянии 120 оборотов?

6) На каком рисунке проведена самая длинная хорда?

1) а; 2) б; 3) в.

7) Диаметр колеса тепловоза равен 180 см. За 2,5 минуты колесо сделало 500 оборотов. С какой скоростью идет тепловоз?

а) не знаю; б) 68 км/ч ; в) 100 км/ч.

О

10бобщение изученного материала по теме: «Отрезки. Конструкции из отрезков».

Практическая работа.

1. Построй круг радиусом 3,4 см. Отметь точки М, N и K, принадлежащие кругу; точки S, P, не лежащие на окружности, ограничивающие этот круг; точки C и D, лежащие на границе круга.

2. На каждом из рисунков отмечены восемь точек. Дорисуй картинку так, чтобы получилось два разных изображения куба.

3. Построй тупоугольный равнобедренный треугольник. Обозначь его. Измерь стороны и найди периметр этого треугольника.

4. Построй два вида цилиндров. Закрась верхнее основание.

5. Построй конус. Нарисуй развертку боковой поверхности.

1. 5

   11) Как называют прибор, с помощью которого измеряют углы?

_____________________________________________

6. Построй угол АОС = 75^; угол ЕКМ = 130. Найди угол АОС и угол СОВ.

7. Угол АОВ = 160^. Угол АОС больше угла ВОС в 3 раза

8) Построй прямоугольный треугольник. Покажи расстояние от вершины прямого угла до противоположной стороны треугольника. Измерь величины всех полученных углов треугольника.

Т

20ЕМА: Измерение углов. Транспортир.

Практическая работа.

1. Построй развернутый угол МОК и проведи внутри него луч ОЕ. Измерь получившиеся углы.

2. Построй тупоугольный треугольник. Измерь его углы.

3. На прямой АВ отметь точки О. Проведи лучи ОС и ОР так, чтобы угол АОС был равен 135^, а угол РОВ был равен 150^. Измерь угол РОС.

4. На рисунке угол АОС= 60^; угол СОВ = 25^. Найди угол АОВ.

6

19) Развивай свою фантазию. Из данных 5 точек построй 2 объемных фигуры и 2 плоских фигуры..

1)

2)

3)

4)

Т

12ЕМА: Отрезки. Конструкции из отрезков.

Контрольная работа.

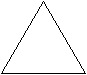
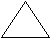
1. Перечисли названия всех изображенных на рисунках фигур.

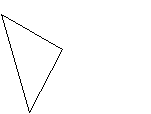
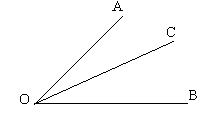
2. Нарисуй какие нибудь две плоские и две пространственные фигуры.

3. Нарисуй какой - нибудь треугольник. Измерь его углы.

4. Охарактеризуй взаимное расположение окружностей с радиусами 2 см и 4 см. Расстояние между центрами которых равно 3 см. Сделай схематический рисунок.

5. Построй три окружности с общим центром.

6. Построй три окружности так, чтобы все они имели хотя бы одну общую точку.

7. На рисунке изображена замкнутая ломаная линия. Попробуй найти её периметр.

4

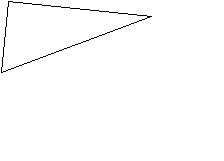
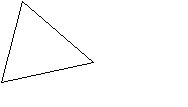
13) А теперь попробуй вычислить площадь треугольника, изображенного на рисунке

1) 6 см²; 2) 3 см²; 3) 9 см².

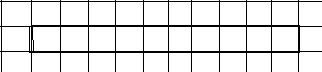
5. Вычисли площадь фигуры на рисунке.

1) 14 см²; 2) 18 см²; 3) 24 см².

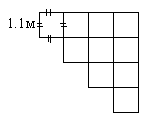
6. Найдите периметр фигуры ABCD, если она составлена из квадратов с площадью 1 ар:

1) 1200 м ; 2) 120 м ; 3) 12 м.

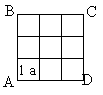
7. Площадь фигуры, составленной из равных квадратов равна:

1) 121 м²; 2) 12,1 м²; 3) 1,21 м²

Т

18ЕМА: Площадь прямоугольника и площадь треугольника.

Тест.

1) Среди этих прямоугольников найди прямоугольник, у которого площадь равна 18 см²

а)

б)

в)

1) а; 2) б; 3) в.

2) Скажи у какого прямоугольника площадь больше.

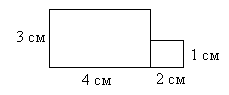
а)

б)

в)

1) а; 2) б; 3) в.

3) В прямоугольном треугольнике 2 противоположные вершины соединены отрезком, который называется диагональю. Эта диагональ делит прямоугольник на два треугольника. Найдите площадь треугольника, если площадь прямоугольника равна 24 см².

1) 24 см²; 2) 12 см²; 3) 18 см².

8

17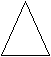) На каждом из рисунков отмечены восемь точек. Дорисуй картинки так, чтобы получилось два разных изображения.

9) Посчитай сколько треугольников на рисунке.

Т

14ЕМА: Сравнение углов. Построение угла равного данному.

Практическая работа.

1. Покажи, какой из этих углов прямой, какой меньше прямого, какой больше прямого.

2. Найди среди этих углов: а) острые; б) тупые; в) прямые.

3. На этом чертеже острые углы закрась одним цветом, а тупые другим

4. Перечисли все углы, которые ты видишь на рисунке.

5

15) Отметь в тетради точки P, S, Q. Начерти угол PQS.

6) Построй луч ОМ. Проведи луч ОК так, чтобы угол КОМ был прямой, и луч ОР так, чтобы угол КОР был острым.

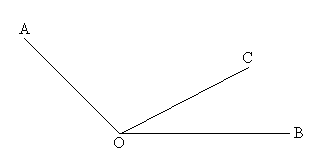
7) На рисунке угол АОС равен углу ЕОD. Сравни углы:

а) угол СОЕ и угол DOA;

б) угол СОА и угол ВОА;

в) угол АОВ и угол DOE;

г) угол DOA и угол ВОА.

16