Технологическая карта урока математики в 10 классе по теме: ' Решение тригонометрических уравнений'

Конспект урока алгебры в 10 классе по теме: «Применение формул тригонометрии при решении уравнений».

Цели и задачи урока:

1) образовательные - сформировать у учащихся умение различать тригонометрические уравнения по способам решения, отработать навыки решения всех видов тригонометрических уравнений; обеспечить их применение при решении задач вариантов ЕГЭ;

2) развивающие - развивать умения работать с книгой, самостоятельно добывать знания; развивать и совершенствовать умения применять имеющиеся у учащихся знания в изменённой ситуации; развивать логическое мышление, умение делать выводы и обобщение;

3) воспитательные - воспитывать трудолюбие, умение общаться со своими сверстниками в процессе работы в парах, аккуратность, культуру поведения, чувство ответственности, способствовать созданию условий для формирования индивидуальной траектории развития профессиональных интересов учащихся, выработке профессионально значимых качеств личности (творческих, организаторских, ораторских).

Напутствие на урок: «Первое условие, которое надлежит выполнять

в математике, - это быть точным,

второе - быть ясным и,

насколько можно, простым».

Л. Карно

Девиз урока: «Не бойтесь формул!

Учитесь владеть этим инструментом

Человеческого гения!

В формулах заключено величие и могущество

разума…» Марков А.А.

Тип урока: урок-практикум, обобщение изученного материала.

Методы обучения: частично - поисковый, исследовательский. Самопроверка.

Формы организации урока: групповая..

Оборудование урока: компьютер, магнитная доска, карточки; рабочие листы, учебники, карточки со словами: синус, косинус, тангенс, котангенс, арксинус, арккосинус, арктангенс, арккотангенс, формулы, уравнения, неравенства, графики. Учебники: Ю.М.Колягин, Ю.В.Сидоров и др. «Алгебра и начала анализа» 10 класс. Раздаточный материал.

Структура урока:

1. Вводно-мотивационная часть.

1.1. Организационный момент.

1.2. Устная работа.

2. Основная часть урока.

2.1. Повторение (чередование фронтальной и индивидуальной форм работы с последующей проверкой задания).

2.2. Знакомство с дополнительными условиями для решения тригонометрических уравнений.

3. Рефлексивно-оценочная часть урока.

3.1. Обсуждение результатов индивидуальной и групповой работы.

3.2. Информация о домашнем задании.

3.3. Подведение итогов урока, рефлексия.

Этапы урока

Учебный материал

Деятельность учащихся

Деятельность учителя

1. Организационный этап.

Задача: подготовить учащихся к работе на уроке.

Проверка домашнего задания.

Приветствие гостей.

На магнитной доске по 1 человеку от групп строят «интеллектуальное дерево» темы.

Отвечают на вопросы и формулируют тему урока, цели урока(слайд 1)

Знакомятся с рабочими листами и поднимают карточку, соответствующую самочувствию ребенка.

Приветствие учащихся.

В это время учитель читает слова напутствие на урок. Слайд 2.

Задает вопросы:

1. Что главное в данной теме

2. Почему выделены некоторые понятия

3. Чем занимались на уроках

4. Как вы думаете, чем займемся сегодня

Сегодня вы работаете в группах, координаторы выбраны. У каждого рабочие листы.

Выясняет, с каким самочувствием каждый начинает урок.

Предлагает написать в рабочем листе: Что знает по теме.

Мотивационный этап.

2. Устная работа (компьютер)

Задача:

актуализировать знания и умения учащихся, которые будут использованы на уроке.

Слайд 4-8

Что называется arcsin а?

Что называется arccos а?

Чему равен arcsin (-а)?

Чему равен arccos (-а)?

Назовите формулу нахождения корней уравнения вида sin x = a.

Назовите формулу нахождения корней уравнения вида cos x = a.

1. Вычислите:

1. arcsin 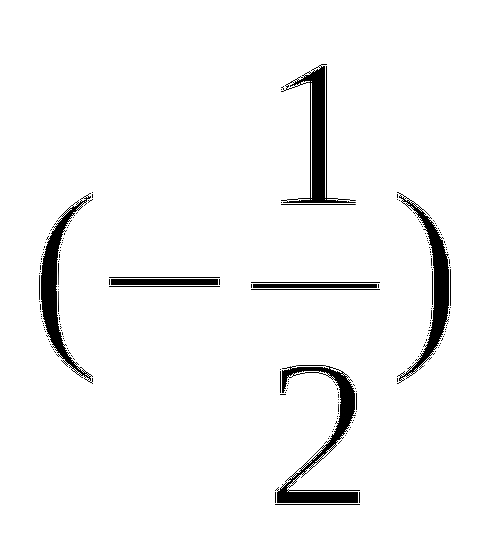; 2) arccos 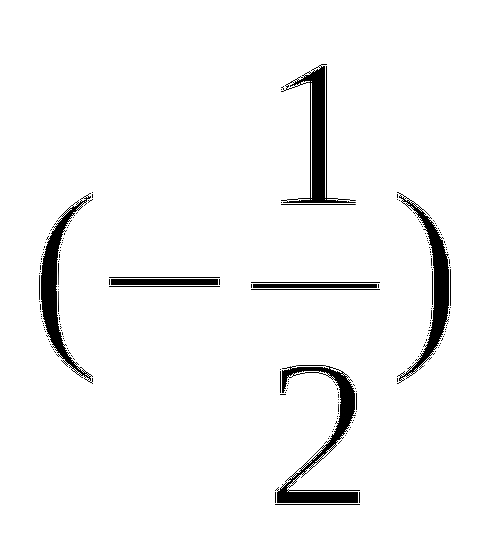; 3) arctg 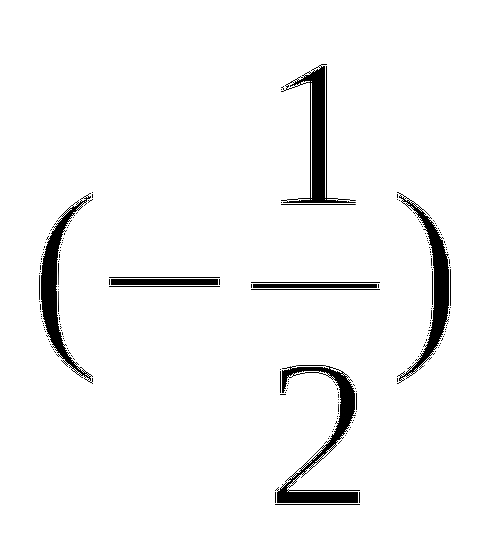; 4) arcsin .

2. Решите уравнения

1) sin x = 1,5; 2) cos x = -2.

4.Найти ошибки в решениях тригонометрических уравнений:

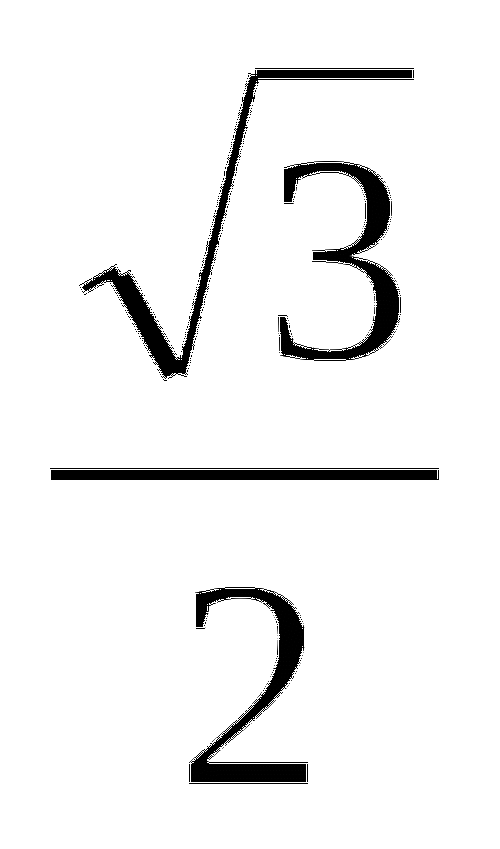
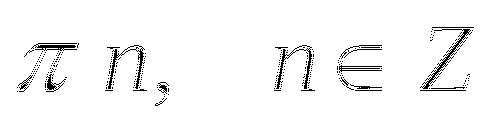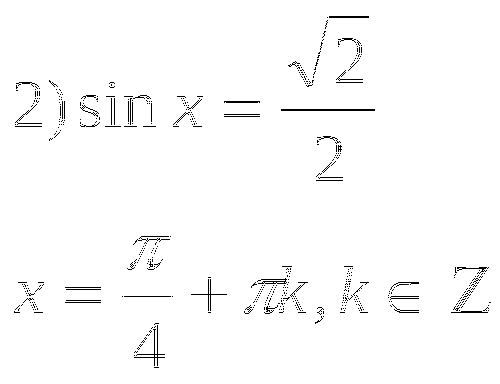(-1^k) _(πk)
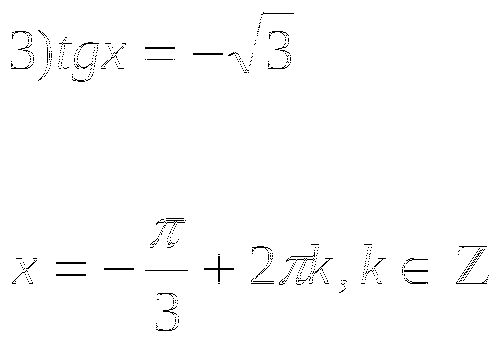(верно) 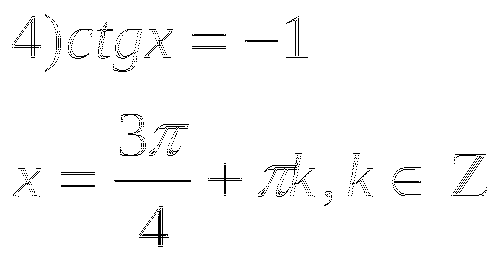_(πk)

sin x = 0, Х= (верно)

5. Может …равным: а) 3,4 , б)П/5 , в)-1,3 ,

6.Устанавливают соответствие.

Сами составляют вопросы для задач.

Отвечают на вопросы.

Делают выводы.

-Что повторили

-Как устанавливают соответствие.

Выставляют оценки в рабочие листы.

Направляет и помогает учащимся подготовиться к дальнейшей работе.

Учитель дает возможность всем высказаться и задать вопрос.

Подводят итог .

Основной этап.

3. Работа в группах «Составь учебник»

Задачи этапа: обеспечивать развитие у учащихся умений анализировать, синтезировать, сравнивать, обобщать, поиск способов решения, отрабатывать навыки самооценки результатов.

На столах лежит лист с перечнем уравнений, лист с перечислением методов решения уравнений, один из них выделен. Группа выбирает уравнения, которые решают данным методом.

Слайд 9.

1-метод замены переменной,

2-метод разложения на множители,

3-метод введения вспомогательного аргумента,

4-метод универсальной подстановки,

5-метод оценки,

6-метод понижения степени.

Вместе работают, выбирают нужный ответ.

Каждая группа отчитывается и все приходят к нужным вариантам.

Предлагает учащимся в каждой группе из предложенных уравнений выбрать только те, которые решаются данным способом.

Руководит проверкой данного задания.

4. Работа в группах: «задача-исследование».

Из списка уравнений решить всем №1.

3-3cosx=2

Все решают в тетрадях и обсуждают ответ на вопрос. Слайд 10.

1-выбрать корни из промежутка [-П ,П]

2- [ 2П ,4П]

3-sinx >=0

4-[-1,5П,0]

5-найти сумму корней (1,7).

На тригонометрическом круге по 1 человеку от группы выходят к доске и объясняют свои варианты ответов.

Оценивают свою работу в Р.Л.

Предлагает каждой группе решить одно уравнение и ответить на дополнительные вопросы.

Подводит итоги.

5. Решение уравнения с дополнительными условиями.

3-3│cosx│=2

Решают, разрабатывают алгоритм решения уравнения с дополнительными условиями.

Решают уравнение и делают вывод, разрабатывают алгоритм решения уравнения с дополнительными условиями.

В вариантах ЕГЭ.

Слово 5 группе. Они изучили варианты за 3 года и пришли к выводу: 12% в работе - это задания с тригонометрией, особое внимание №15. Всем группам раздают задания.

Как можно изменить уравнение, чтобы рассмотреть дополнительные условия.

Где используем дополнительные условия.

Cлайд 11

6. Применение тригонометрии.

Подготовлен небольшой материал по группам:

тригонометрия и геометрия, биология, астрономия и космос.

Учитель:В современных программах подготовки экономистов, финансистов и т.д. курс математики уверено занял одно из ключевых мест. В частности тригонометрия как один из разделов математики находит широкое практическое применение по следующим специальностям: "Финансы", "Экономика, бухгалтерский учет и аудит", "Маркетинг", "Правоведение"

7. Домашнее задание.

1. Найти еще способы решения тригонометрических уравнений.

2. Решить уравнение с доп. условиями из задач вариантов 5-8 выбрать.

3. №888, 932(1,2)

8. Что записано

1. cosx = 3a - 7

2. cosx = (3a - 7)²

3.|cosx| = 3a - 7

4.

Предлагают свои варианты.

Слайд 12.

Какие уравнения записаны?

Добавьте еще уравнение?

Эта работа будет продолжена на следующем уроке.

9. Рефлексия.

Слайд 15.

Отвечают на вопросы, дают оценку своей работе и подводят итог.

Заполнить таблицу: что узнал и что хотел бы узнать.

Продолжи фразу

«Сегодня на уроке я повторил…»

«Сегодня на уроке я закрепил…»

«Сегодня на уроке я понял…»

« Мне надо..»

Сдают рабочие листы.

Поднимают цветные карточки.

Покажите, с каким самочувствием заканчиваете урок.