Библиотека функций для 10-11 классов общеобразовательной школы

Библиотека функций для 11 класса

Введение.

В данном методическом пособии рассматриваются вопросы решения практических аспектов в алгебре общеобразовательной школы с помощью электронных таблиц. В работе представлены примеры построения графиков функций различных типов, приемы оформления в электронных таблицах (программа EXCEL), решение уравнений графическим методом, а также представлен метод решения алгебраических и трансцендентных уравнений методом подбора параметров.

Цель данной работы - дать наглядную интерпретацию в вопросах построения графиков и решения уравнений, создать минимальную библиотеку построения графиков в электронных таблицах.

Данное пособие знакомит учителей математиков с автоматизацией при построении графиков и решении уравнений в курсе средней школы,

а также может быть весьма полезным материалом при проведении уроков.

Наглядное содержание материала может оказать помощь учащимся
при подготовке к единым государственным экзаменам.

1. Построение графиков функций.

Подготовленные таблицы для графиков и решения уравнений , а также сами графики выполнены в программе EXCEL (Приложение 1.).

Материал распределен по отдельным листам (1, 2, 3 и т. д.) которые вызываются через ярлычки на строке «статус». На ярлычках даны также названия построенных графиков. Для вызова Приложения 1 достаточно вызвать гиперссылку.

Лист1. Приложение 1.

Область определения для построенных функций задана в радианах, дан перевод градусов в радианы. На листе 1. Приложения 1. представлены расчетные таблицы и графики функций вида: y= sinx, y= sin10x, y= sin(x/2), y=cosx, y= cos10x, y=cos(x/2), y=tgx, y=asinx. На графиках наглядно видны изменения-трансформации производных графиков относительно стандартных: y= sinx , y= cosx. Эти изменения в производных графиках представлены в виде амплитуды или периода. Графики тригонометрических функций наглядно демонстрируют гармоническую форму -симметричность, повторяемость (периодичность) и плавность изменения значений функции. Для сравнения на листе 1 представлены графики показательных функций у=2^x и y=(1/2)^x. Дополняя друг друга графики образуют симметрию относительно оси Y, но не являются гармоническими функциями. Здесь же дается пример слияния двух функций y= -2cosx и y=1/2x⁴. Графики строятся по условию x<0 и x>0.

Лист 2. Приложение 1.

Область определения для построенных функций задана в радианах, дан перевод градусов в радианы. На листе 2. Приложения 1. представлены расчетные таблицы и графики функций вида: трансформированный синус y=- 3sin(x+pi/2) и y=1/2sin(x/2+pi/6), построены графики по условию 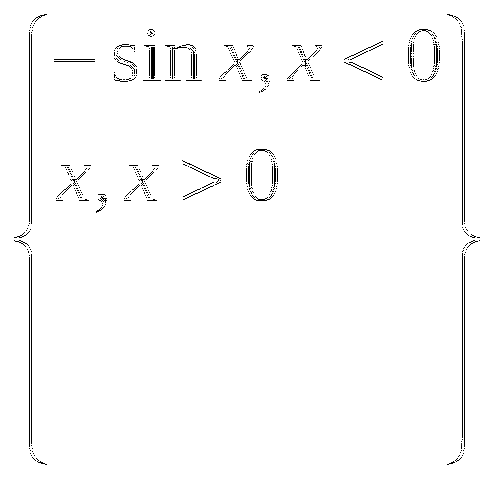Построены графики иррациональных функций y=корень(x) и y=корень(2х). Далее даны графические решения для уравнений

tgx= - корень(3), -cosx=3x-1.

Лист 3. Приложение1.

На листе представлены графики нечетных функций : y=3x-x³ , y=x⁵ -x³ и график четной функции: y=x⁶ -x⁴ . При построении этих графиков особое внимание уделяется масштабу шкал по оси Y и Х, иначе вид графиков будет неверный. Далее рассмотрен график многочлена для четной и нечетной функции: y= -x³ +6x²-5. Здесь же представлены графики обратной функции y=1/x и смешанной функции y= x+4/x; представлены графики дробно-линейных функций вида: y=(2x-3)/(3x+2); y=1/(x²+2x+1).

Интерес представляет сложение графиков иррациональной и линейной функций вида: y=2*корень(х)-x.

Наконец здесь рассмотрены графики функций, содержащие переменную под знаком модуля: y= |x|+2 или графики, содержащие значение фунции под знаком модуля: y=|x+2|; y=|sinx|; y=| x³-3x|.

Лист 4. Приложение1.

На данном листе построены таблицы и графические решения следующих уравнений: x³-3x=(x+1)⁶+2; x^1/4=(x+3)^1/7 ; x^1/3=7-6x. (Необходимо выделять указанные диаграммы с решениями уравнений , для того чтобы просмотреть координаты точек пересечения данных графиков т. е. увидеть решение данного уравнения.) Здесь же построены графики степенных функций с показателями а>1 и а<1 :y=корень(x+3)+4; y=(x+6)^7/4 +2.

Лист5. Приложение 1.

На этом листе представлены таблицы и графики для решения уравнений

графическим методом : x^1/6=|x|; 1/x= x^1/2; 2^x-1=корень(х); 5^x=-2x+5.

При наведении курсора на точку пересечения графиков автоматически выводятся координаты точки пересечения, т.е. показывается корень решения данного уравнения.

Далее рассмотрены таблицы и графики функций, построенные по условию: y=2; y=2x²; y=x^3/2. В результате слияния различных графиков получен единый график. На листе 5. представлены таблицы и графики показательных убывающей и возрастающей функций: y=5^x+1; y=(2/3)^x+0,5.

2. Задачи, приводящие к выделению различных областей на плоскости в системе координат.

Лист1. Приложение 2.

В качестве иллюстрации выделения различных областей, ограниченными линиями, построены таблицы и графики : a) y=x³ ; y=x². b) y=x² ; y=4-x². c)y =корень(х); y=4x² d) x² +y² =a²; x² +y² =b²

e) y=x; y= -x; y=0; f) y=1-x; y=x+1; g) y=x;y=x+3;y=-2x+5; y=-2x+1.

Данный набор графиков хорошо иллюстрирует выделения различных областей на
плоскости в системе координат для решения неравенств или вычисления интегралов.

2. Примеры сложения графиков функций

Лист2. Приложение 2

Особое внимание при построении графиков функций уделяется методу сложения графиков. Этот вопрос рассматривается обычно в технических аспектах.

Приведем примеры сложения графиков простейших тригонометрических функций: y=sinx +cosx; y=sin⁶x+cos⁶x; Второй график демонстрирует максимальное и минимальное значение четной тригонометрической функции. Для сравнения предложен график нечетной тригонометрической функции: y=sin³(x) +cos³x.

В дополнение здесь приведен интересный график трансформированной тригонометрической фунции: y=|2sin(2|x|-pi/4)|.

В качестве примера сложения графиков функций предложена задача сложения трех гармонических колебаний в контуре генератора:

Y=5cos1000x; y=10cos(1000+30)x; y=10cos(1000-30)x.