Урок обобщения и систематизации знаний по теме 'Разложение на множители' (7 класс)

Здоровьесберегающий урок обобщения и систематизации знаний по теме "Разложение на множители" (7 класс)

Соловьева А.В., учитель МОУ СОШ №10

г. Дзержинска Нижегородской области

Методические комментарии.

Предлагаемый урок является первым уроком из трех, отводимых на изучение темы "Применение нескольких способов раложения на множители". В роли учителя при обобщении и систематизации материала по данной теме выступают сами учащиеся, поэтому подготовку к уроку начинается заранее. Учащиеся делятся на три группы, каждая группа работает с одним способом разложения. Группы готовят задания типа:

• решить по алгоритму;

• применение данного способа разложения при решении различных типов заданий.

Предложенные задания должны быть доступны для коллективного решения и ярко демонстрировать каждый теоретический факт. Каждая группа получает шаблон систематизирующей таблицы и продумывает вариант оформления соответствующего столбца в программе WORD. Учитель одобряет вариант или вносит коррективы в конечный вариант оформления столбца таблицы. Для каждой группы учитель делает заготовку рабочего слайда в СМАРТ-презентации, используя инструмент "фотоаппарат". От каждой группы выбирается "учитель" с ассистентом. Совместно с учителем продумывается система вопросов по блоку, предполагаемые ответы учащихся, вариант заполнения столбца шаблона таблицы.

Общая схема работы на уроке заключается в следующем: в ходе повторения основных алгоритмов и выполнения системы заданий составленных одной из групп, происходит повторение основных теоретических положений, связанных с разложением на множители. В процессе работы происходит постепенное заполнение шаблона таблицы на рабочих местах учащихся и заполнение пустых мест на слайдах СМАРТ-презентации, отражающих основные сведения о способах разложения и их применении.

Таким образом, выстраивается система, демонстрирующая большую работу, проделанную школьниками при изучении данной темы. Учащиеся понимают, что в результате изучения данной темы они вооружились еще одним способом решения математических задач через разложение на множители. Осознание важности проделанной работы служит эмоциональным стимулом к продолжению изучения последующих разделов алгебры. Учитель намечает перспективу в изучении более сложных уравнений, подчеркивая, что "Разложение на множители" является одним из общих приемов решения уравнений всех типов.

Конспект урока

Тема урока. Способы разложения на множители.

Тип урока. Урок обобщения и систематизации знаний.

Цели урока. Привести в систему знания о способах разложения, выявить типы задач на их применение.

В результате урока ученик

знает:

что значит разложить алгебраическое выражение на множители;

алгоритмы способа вынесения общего множителя за скобки, способа группировки, использования формул сокращенного умножения;

формулы сокращенного умножения

умеет:

раскладывать алгебраические выражения на множители, применяя один из способов;

решать уравнения путем разложения на множители;

доказывать делимость через разложение на множители;

находить рациональным образом значения алгебраических выражений

осознает:

природу происхождения данной темы;

роль обобщения, систематизации и классификации в получении новых знаний;

значимость темы в курсе алгебры, ее роль для дальнейшего построения курса

Структура урока

1.Мотивационно-ориентировочная часть.

1.1 Мотивация.

1.2 Постановка учебной задачи (цели) урока.

1.3 Планирование учебной деятельности.

2. Операционно-познавательная часть.

2.1 Обобщение и систематизация знаний об отдельных способах разложения на множители.

2.2 Выявление общих типов математических задач на применение способов разложения.

2.3 Анализ построенной системы.

3. Рефлексивно-оценочная часть.

3.1 Оценка и самооценка учебной деятельности.

3.2 Подведение итогов урока.

3.3 Планирование предстоящей учебной деятельности.

Ход урока

Деятельность учителя

Деятельность ученика

1. Мотивационно-ориентировочная часть

1.1. Мотивация

- Здравствуйте, ребята! Мы собрались сегодня на уроке, чтобы подвести итог большой работы.

Все это время какими преобразованиями алгебраических выражений мы занимались?

- Мы умножали многочлен на одночлен, многочлен на многочлен, раскладывали алгебраические выражения на множители.

- Что значит разложить на множители?

Слайд 1 (объекты в движении)

- Разложить на множители - значит представить в виде произведения одночленов и многочленов.

- И это делать мы умеем не единственным способом. Как быть с таким "ворохом" знаний о разложении? Что вы делаете, когда в вашей комнате накапливается много-много разных нужных вещей?

- Мы наводим порядок, раскладываем их по местам.

- Вот и у нас накопилось столько знаний, что пора навести в них порядок, подвести итог всему, что мы знаем о разложении на множители.

- Какие известны способы разложения на множители?

Слайд 1 (объекты в движении)

Способы:

• вынесение общего множителя за скобки;

• способ группировки;

• использование формул сокращенного умножения

- Классифицируйте примеры алгебраических выражений по способам.

-Как разложить и где мы сталкиваемся с необходимостью в разложении ??? Знаний много, их нужно упорядочить.

Слайд 1 (объекты в движении)

Учащиеся размещают объекты в один из столбиков, соответствующих способу разложения:

1.2 Постановка учебной задачи(цели) урока

- Предлагаю посвятить этому занятию сегодняшний урок. Запишем тему урока "Разложение на множители".

(Ученики записывают тему в тетрадях)

- А как сформулировать цель урока?

- Привести в порядок знания о приемах разложения.

- В науке, когда речь идет об упорядочении каких-то знаний, используют оборот "привести знания в систему". Давайте используем этот оборот в формулировке цели. Как будет звучать цель?

- Привести в систему знания о способах разложения.

1.3 Планирование учебной деятельности

- Не только цель урока будет звучать непревычно, сам урок будет необычным.

Сегодня вы попробуете себя в роли учителя. Это очень непросто. Поэтому "учителей" будет несколько, каждый проведет часть урока. Учителя готовились к уроку вместе со своей группой ассистентов. Им известен порядок их выступления. А что делать остальным?

- Слушать, отвечать на вопросы, решать упражнения (если необходима помощь, то можно обратиться к ассистенту)

- И не только это. Перед вами на партах лежит канва таблицы, такая же заготовка фрагментарно сделана на экране интерактивной доски. В ходе урока мы должны заполнить таблицу полностью, но делать это будете только вместе с "учителем".

- Все согласны принять правила работы?

Тогда начинаем постепенно заполнять графы таблицы. Как только таблица будет заполнена, мы постараемся связать ее графы и обсудим результаты работы.

2. Операционно-познавательная часть

2.1 Обобщение и систематизация знаний об отдельных приемах разложения

- Право руководства классом передается представителю первой группы.

- Первый способ - вынесение общего множителя за скобки. Повторим шаги алгоритма и применим для разложения первого выражения.

(Проговаривают действия и результаты записывают в таблице. "Учитель" работает со слайдом 2 и заполняет пустые места. Ученики заполняют постепенно первый столбик таблицы).

-Проиллюстрируем на более сложных примерах.

(Вместе с "учителем" решают примеры на все частные случаи. Ученики переключаются на следующий фрагмент таблицы).

- Итог: мы повторили, как работает алгоритм в различных случаях. Ответили на вопрос как???

- А теперь где, при решении каких задач? Выделим типы задач на применение первого способа. Слово ассистенту №1.

- Решите уравнение. Умеем ли решать уравнения такого типа. Обнаруживаем, что слева выражения знакомого нам вида, справа нуль. Какое преобразование помогает упростить уравнение? На какую мысль вас наталкивает справастоящий нуль?

- Мы умеем решать только линейные уравнения и сводимые к ним. Левую часть можно разложить на линейные множители. Вспомним свойство произведения, равного нулю: произведение равно нулю, если хотя бы один из множителей равен нулю, а другой при этом не теряет смысл.

- Решим уравнение

1. Решить уравнение

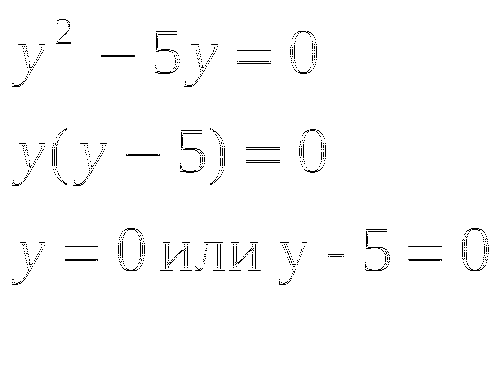
y=0 или y-5=0

y=5

Ответ:0;5.

(Ученики вместе с ассистентом решают уравнение, заполняя фрагмент таблицы, слайд 3).

- Для закрепления решите уравнение 2. (Ассистенты первой группы работают консультантами. Один из желающих работает у доски, пишет маркером). Результаты проверяются по окончании работы.

Слово ассистенту №2

2x(4x+3)=0

x=0 или 4x+3=0

x=-0,75

Ответ:0; -0,75.

- Что значит выражение кратно натуральному числу?

- Кратно - значит делится на данное натуральное число.

- Доказать, что числократно 9

- Какое известно утверждение в математике для доказательства делимости? Какого условия достаточно, чтобы утверждать делимость?

1. Если один из множителей делится на данное натуральное число, то и все произведение делится на это число.

2. Если каждое слагаемое суммы делится на данное натуральное число, то и сумма делится на это число.

- Каким из утверждений воспользуемся для доказательства делимости?

- Явно, что можно попробовать использовать первое утверждение. Но прежде надо выражение представить в виде произведения.

-Докажем.

Сначала разложим способом вынесения на множители.

=(2³)⁶+2¹⁵=2¹⁸+2¹⁵=2¹⁵(2³+1)=2¹⁵∙9

Т.к. один из множителей делится на 9, значит и произведение делится на 9.

(Ученики вместе с ассистентом доказывают делимость, заполняя фрагмент таблицы, слайд 3)

- Итак, подведем итог работы с первой группой. Вынесение общего множителя - один из приемов разложения алгебраических выражений на множители. Его применение основано на распределительном свойстве умножения. Вынесение общего множителя используем при решении уравнений, нахождении значений числовых выражений рациональным способом и доказательстве делимости.

- Спасибо за подробную работу. Благодарю всех ребят первой группы, которые так тщательно подготовили материалы для этой части урока. А нам пора переходить к следующему способу.

2.2. Установление связей между способами разложения.

Другие способы рассматриваются аналогичным образом. В процессе работы заполняются остальные графы таблицы. Параллельно для самопроверки оформляются слайды 4,5,6,7. Анализируя столбцы таблицы, ученики выявляют типичные задания.

2.3. Анализ построенной системы

- Итак, мы заполнили таблицу полностью. Давайте обсудим полученный результат. Что отражено в таблице?

- В таблице отражены сведения о существующих способах разложения на множители. Таблица напоминает теоретическую шпаргалку. Ею можно воспользоваться в случае, если что-то забыл. На нее можно опереться при решении задач. Она служит опорным конспектом.

3. Рефлексивно-оценочная часть

3.1. Оценка и самооценка учебной деятельности

- Действительно, заполненная таблица имеет множество достоинств. Она, я бы сказала, получилась полезной и гармоничной. И все вы хорошо потрудились над ее созданием.

Прошу вас на маленьких листочках :

поставить себе оценку за работу на уроке и при подготовке к нему;

оценить подготовительную работу каждой из трех групп.

3.2. Подведение итогов урока

- Итак, при постановке цели урока мы использовали оборот "привести знания в систему". Достигнута ли поставленная нами цель или нет, зависит от того, построена ли система знаний. Как вы считаете?

- Мы привели знания в систему, потому что повторили все основные сведения о способах разложения и их применении при решении практических задач. Доказательством является заполненная таблица.

3.3. Планирование предстоящей учебной деятельности

- Чаще приходится применять одновременно несколько приемов разложения. Выработать стратегию действий нам предстоит на следующем уроке.