Урок алгебры для 9 класса «Методы решения систем уравнений»

А - 9, Методы решения систем уравнений

Цели:

• систематизировать знания по теме;

• формировать навыки сознательного выбора и способа решения систем уравнений;

• развивать потребности в нахождении рациональных способов решения систем уравнений;

• развивать познавательный интерес к предмету.

Формирование компетенций: компетенции самосовершенствования - саморегулирование и саморазвитие, речевое развитие (через самостоятельную и устную работу, формулировка выводов); компетенции социального взаимодействия - сотрудничество; компетенции в общении - устном, письменном; компетенции познавательной деятельности - постановка и решение познавательных задач; компетенции информационных технологий - приём, переработка и выдача информации, компьютерная грамотность.

Тип урока: урок обобщения знаний.

Средства обучения: компьютер, медиапроектор, интерактивная доска; слайдовая презентация.

Формы организации учебной деятельности: индивидуальная, коллективная, диалог, работа с текстом слайда, работа в тетради, парная.

Методы: наглядный, словесный, графический (практический).

Методы мотивации: поощрение, порицание; побуждение к поиску решения; предъявление учебных требований, прогнозирование будущей деятельности, самооценка деятельности; создание ситуации взаимопомощи, заинтересованность в результатах коллективной работы.

Место проведения урока: МОБУ СОШ №20, для учащихся 9-х классов четырёх школ посёлка в рамках предпрофильной подготовки (присутствовало на уроке 37 учеников, все учащиеся (кроме двоих), учителю не знакомы).

Ход урока:

I. Организационный момент

- Здравствуйте, ребята! Сегодня урок по важной теме: «Решение систем уравнений».

Нет таких областей знаний в точных науках, где бы ни применялась данная тема. Эпиграфом к нашему уроку являются следующие слова: «Ум заключается не только в знании, но и в умении прилагать знания на деле». (Аристотель)

- Сегодня на уроке мы: Повторим методы решения систем уравнений и систематизируем знания по теме.

II. Фронтальный опрос

- Для того, что бы успешно решать системы уравнений, давайте вспомним:

1). Что называется системой уравнений? (Системой уравнений называется несколько уравнений, для которых требуется найти значения неизвестных, удовлетворяющих одновременно всем этим уравнениям).

2). Что значит решить систему уравнений? (Решить систему уравнений, значит найти все решения или доказать, что решений нет).

3). Что называется решением системы уравнений? (Решением системы уравнений называют пару чисел (x; у), при которой все уравнения системы обращаются в верные равенства).

4) Выясните, является ли решением системы уравнений пара чисел: а) х = 1, у = 2; (-) б) х = 2, у = 4; (+) в) х = - 2, у = - 4? (+)

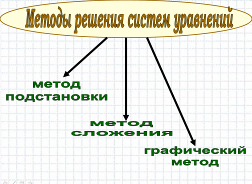
5). Какие методы решения таких систем уравнений вы изучили? (Графический метод, метод подстановки, метод сложения, метод замены переменной).

III. Выполнение практической работы

- Давайте напомним себе, на что нужно обратить внимание, при выборе метода решения системы уравнений? (Если в каком-либо уравнении можно выразить одну переменную, через другую, то применяем метод замены переменной. Если в уравнениях можно уравнять коэффициенты при одинаковых переменных, или эти коэффициенты с противоположными знаками, то применяем метод сложения).

- Повторим! (две системы - заполнить пропуски; один человек - за компьютером, можно вывести шаблон на интерактивную доску, ресурс в программе stratum, ; остальные - по карточкам, затем - проверка). ЕХЕ файлы (нужна программа Stratum2000) взяты из Единой коллекции цифровых образовательных ресурсов на сайте http://school-collection.edu.ru.

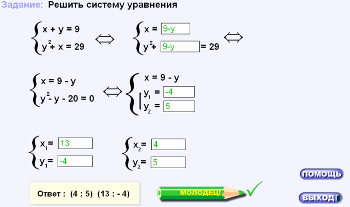
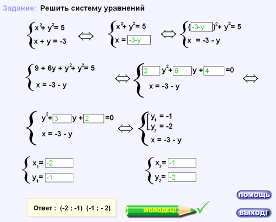
IV. Работа в тетрадях

- А теперь работаем самостоятельно. (Два человека работают у доски для последующей проверки). Выберите способ решения и решите систему:

а) б)

х² + х - 30 = 0,

х₁ = - 6, значит, у₁ = 15; 2у² + 3у - 5 = 0,

х₂ = 5, значит, у₂ = 4. у₁ = 1, значит, х₁ = 4;

Ответ: (- 6; 15); (5; 4). у₂ = -5, значит, х₂ = -8.

Ответ: (4; 1); (- 8; - 5).

- В чем заключается графический метод решения систем уравнений? (Строятся графики каждого из уравнений. В зависимости от того, сколько точек пересечения имеют графики, столько решений и будет иметь система уравнений).

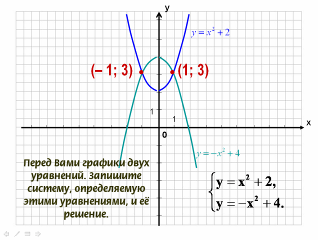
- Перед Вами графики двух уравнений. Запишите систему, определяемую этими уравнениями, и её решение.

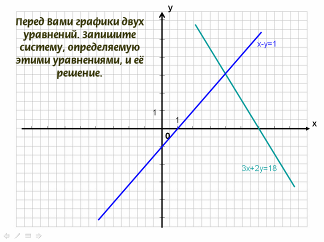
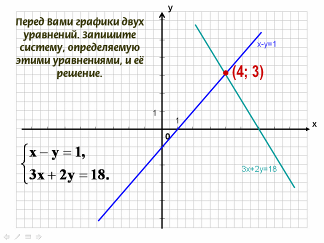
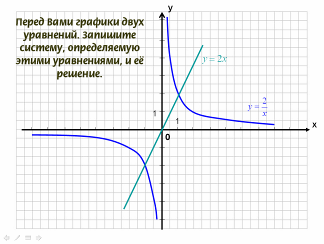
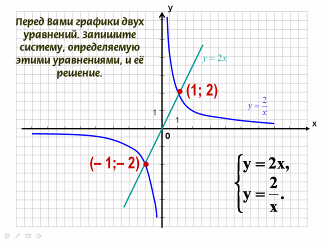
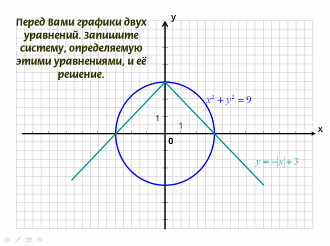
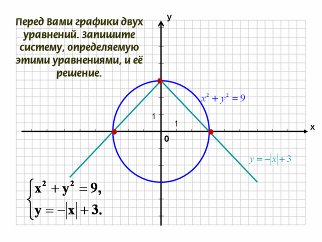
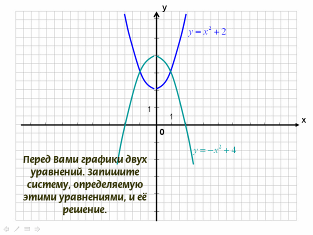
- Какие из перечисленных систем можно решать с помощью данного рисунка?

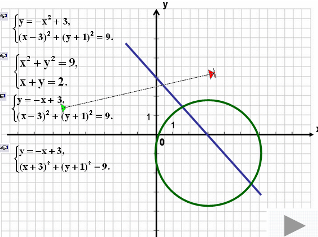
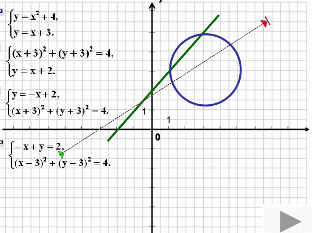
- Были даны 4 системы, их нужно было соотнести с графиками. Сейчас задание обратное: есть графики, их нужно соотнести с системой.

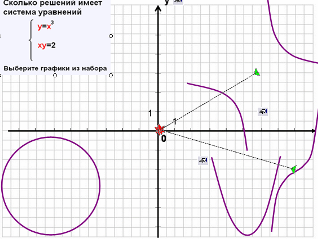
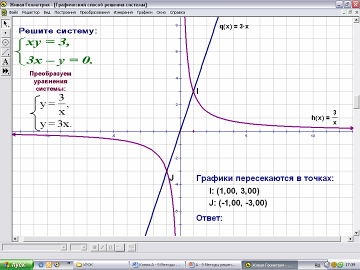
- Подведём итог решения систем графическим методом. (Ссылка на Живую геометрию). Один человек работает за компьютером в программе «Живая геометрия», остальные - самостоятельно в тетрадях, в парах.

V. Пропедевтика

- Решим систему уравнений:

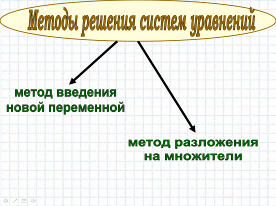
- Какой из известных способов можно применить? (Учащиеся рассуждают, делают выводы, что ни один из известных способов здесь не применим). Проблема?

- Существуют и другие способы решения систем уравнений, которые вы будете применять при решении систем уравнений: это метод введения новой переменной и метод разложения на множители.

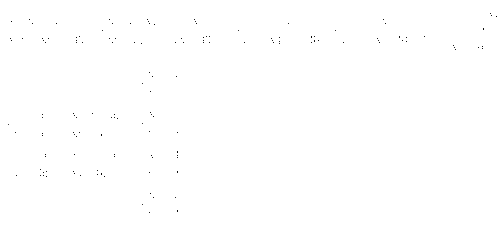Ответ: (5; 1); (1; 5); (3; 2); (2; 3).

VI. Итог урока. Рефлексия