- Учителю
- Конспект урока по геометрии в 8 классе 'Прямоугольник. Ромб. Квадрат. '
Конспект урока по геометрии в 8 классе 'Прямоугольник. Ромб. Квадрат. '
Конспект урока по геометрии 8 класс " ПРЯМОУГОЛЬНИК. РОМБ. КВАДРАТ"
-
Цели: ввести понятие ромба и квадрата; изучить их свойства. развитие памяти, внимательности, формирование умений обобщать, сравнивать, оценивать, анализировать, увеличение степени развивающего воздействия на формирование личностных качеств обучаемых, развитие инициативы, познавательного интереса, формирование чувства ответственности, увеличение степени дисциплинированности, организованности. увеличение развивающих способностей, развитие нестандартного мышления, использование личностного и субъектного опыта, стимулирование «я - концепции», внедрение ситуации «успеха» в образовательный процесс, развитие индивидуальных особенностей учащихся, развитие умений применять математические знания для решения практических задач.
Ход урока
I. Проверка домашнего задания.
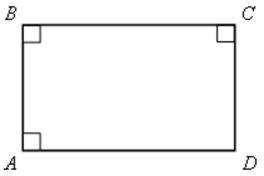
1. АD ![]() АВ, ВС
АВ, ВС ![]() АВ (по условию), тогда АD || ВС (как два перпендикуляра к одной прямой).
АВ (по условию), тогда АD || ВС (как два перпендикуляра к одной прямой).
2. АВ ![]() ВС, СD
ВС, СD ![]() ВС (по условию), тогда АВ || СD (как два перпендикуляра к одной прямой).
ВС (по условию), тогда АВ || СD (как два перпендикуляра к одной прямой).
3. Так как АD || ВС и АВ || СD, тогда АВСD - параллелограмм (по определению).
4. ![]() D =
D = ![]() В (как противолежащие углы параллелограмма).
В (как противолежащие углы параллелограмма).
5. В параллелограмме АВСD: ![]() А =
А = ![]() В =
В = ![]() С =
С = ![]() D = 90°, значит, АВСD - прямоугольник (по определению).
D = 90°, значит, АВСD - прямоугольник (по определению).
Выполнить задания (устно):
1) Найдите боковую сторону равнобедренного треугольника, высота которого равна 6 см, а угол при вершине равен 120°.
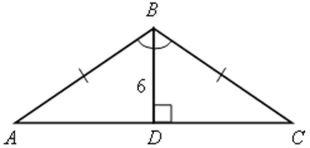
![]() А = 30°, АВ = 2ВD = 12 (см).
А = 30°, АВ = 2ВD = 12 (см).
2) Диагонали параллелограмма взаимно перпендикулярны.
Докажите, что все его стороны равны.
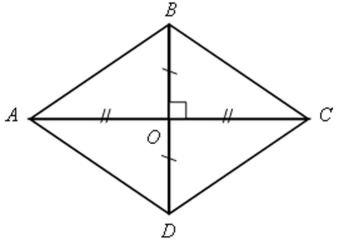
![]() ВОС =
ВОС = ![]() DОС =
DОС = ![]() ВОА =
ВОА = ![]() DОА по двум катетам.
DОА по двум катетам.
Имеем АВ = ВС = DС = АD.
II. Изучение нового материала.
1. Определение ромба.
2. Так как ромб - параллелограмм, то какими свойствами он обладает?
3. Какими особыми свойствами обладает ромб?
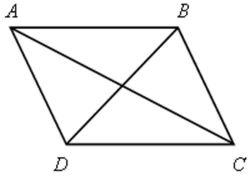
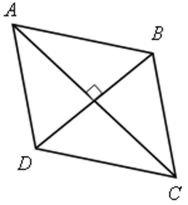
4. Доказательство свойств ромба:
а) диагонали ромба взаимно перпендикулярны;
б) диагонали являются биссектрисами углов.
5. Будут ли верны обратные утверждения? Докажите.
6. Определение квадрата как прямоугольника, у которого все стороны равны.
7. Определение квадрата как ромба, у которого все углы прямые.
8. Так как квадрат является ромбом и прямоугольником, то он обладает их свойствами. Перечислите их.
III. Решение задач.
№ 405 (а).
а) АВ = ВС = АС, ![]() АВС - равносторонний,
АВС - равносторонний, ![]() А =
А = ![]() В =
В = ![]() С = 60° в ромбе
С = 60° в ромбе ![]() АВС = 60°,
АВС = 60°, ![]() ВАD = 120°.
ВАD = 120°.
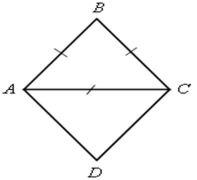
№ 410 (а, б) признаки квадрата.
IV. Итоги урока.
Свойства ромба
АВСD - ромб
![]()
АВ || CD, ВC || АD,
![]() А =
А = ![]() С,
С, ![]() В =
В = ![]() D,
D,
АО = ОС, ВО = ОD
свойства параллелограмма
АВ = ВC = CД = АD
АС ![]() ВD
ВD
АС - биссектриса ![]() А
А
ВD - биссектриса ![]() В
В
все стороны равны
диагонали перпендикулярны
каждая диагональ - биссектриса углов ромба
АВСD - ромб
![]()
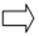
Признаки ромба
АВ = ВС = СD = АD
![]()
АВСD - ромб
АВСD - параллелограмм
АС ![]() ВD
ВD
![]()
АВСD - ромб
АВСD - параллелограмм и АС - биссектриса ![]() А
А
![]()
АВСD - ромб
Свойства квадрата
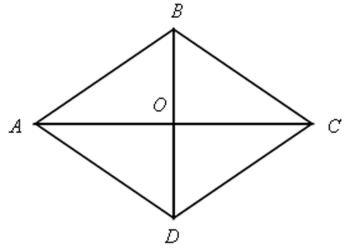
АВСD - квадрат
АВ || CD, ВC || АD
АВ = ВC = CD = АD
![]() А =
А = ![]() В =
В = ![]() C =
C = ![]() D = 90°
D = 90°
АО = ВО = CО = DО
АС ![]() ВD
ВD
АС, ВD, СА, DВ - биссектриса угла
все стороны равны
все углы прямые
отрезки диагоналей равны
диагонали перпендикулярны
каждая диагональ является биссектрисой угла
Признаки квадрата
Для того чтобы доказать, что данный четырехугольник является квадратом, можно:
-
доказать, что четырехугольник является прямоугольником с равными сторонами;
-
доказать, что четырехугольник является ромбом с прямыми углами.
Домашнее задание: вопросы 14-15, с. 115; №№ 405 (б), 409.