- Учителю
- Урок «Решение задач» геометрия 8 класс
Урок «Решение задач» геометрия 8 класс

Подготовила и провела учитель математики:
Цветинская Галина Александровна.

АСТАНА - 2013-2014 учебный год

Вдохновение нужно в геометрии,
как в поэзии.
А.С. Пушкин.
МАТЕМАТИЧЕСКИЙ МАРАФОН: СМЕЛОСТЬ И ЛОВКОСТЬ ПРОТИВ «КОКЕТСТВА»
Цель: Обобщить единичные знания, привести их в систему
Задачи:
-
Практическое применение умений и навыков вычисления площадей фигур, по формулам применяя значения синуса, косинуса, тангенса острого угла.
-
Развивать самостоятельность учащихся, используя творческие задания.
-
Повысить интерес к математике, снять усталость, способствовать развитию внимания.
-
Прививать чувство товарищества, взаимопомощи.
Оборудование: Интерактивная доска, оценочный лист индивидуальный,
и для групповой работы.
Класс поделен на две группы, которые будут соревноваться, и группа поддержки (оставшаяся часть класса).
Для того чтобы связывать теорию с
практикой, с повседневной и всесторонней
работой на общую пользу, для того надо
много и самостоятельно работать.
Н.К. КРУПСКАЯ.
Ход урока:
-
Организационный момент.
-
Презентация команд: команды в произвольной форме создают презентацию о себе с использованием интерактивной доски.
-
Урок поделен на конкурсы.
-
Рефлексия
I конкурс: Разминка.
(разминка поделена на три флипчарта так, чтобы удобно было выполнить на оставшемся пространстве данные задания. )
-
Какой формулой определяется площадь параллелограмма? Сделать соответствующий чертёж и указать элементы из написанной формулы.
-
Площадь, какой фигуры определяется с помощью формулы Герона? Напишите её.
-
Как определяется площадь трапеции? Сделайте чертеж и укажите элементы.
-
Как определяется площадь треугольника, если заданы основания и высота, опущенная на это основание? Сделайте чертеж и укажите элементы.
-
Как определить площадь треугольника по двум сторонам и углу между ними? Сделайте чертеж и укажите элементы.
-
Найдите площадь параллелограмма, если заданы две его стороны 7 см, и 12см и угол между ними - 300.
Подведение итогов по конкурсу.
II конкурс: Старт.
Команды на время решают задачу:
1. Найдите катеты и второй острый угол прямоугольного треугольника по гипотенузе равной 13 см и острому углу ![]() .
.
2. Диагональ параллелограмма равна 10см и делит его на два равных треугольника с периметрами, равными 36см. Найдите периметр параллелограмма.
Задания для группы поддержки:
-
Найдите площадь треугольника со сторонами равными 6см и 5см и углу между ними 600.
-
Найдите площадь трапеции с основаниями 5см, 11см, и высотой 7см.
-
Сторона параллелограмма равна 14см, а высота, опущенная на неё равна 10см. Найдите его площадь.
Подведение итогов по конкурсу.
III конкурс: Забег. (Кто быстрее).
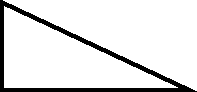
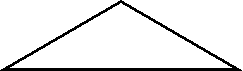
Найдите площади данных фигур:
A
B
-
13
 2)
2)
300
12
C
B
9
A
C
8
B
B
13
2 3) 4)
3) 4)
14

C
C
B
15
A
A
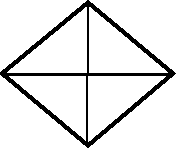
C
B5) 6)

C
A
10
600
15
D
A
D
3
C
B
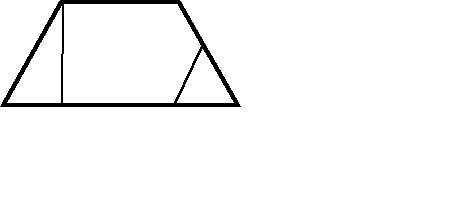 Дано: АС=8, BD=5
Дано: АС=8, BD=5
7
E
5)
2
F
D
A
Дано: AB||FE
Нахождение площадей данных фигур выполняется на скорость решения и надо за определенное время решить большее количество задач. Группа поддержки также решает данное задание, и может свои заработанные баллы отдать той или иной команде.
Подведение итогов по конкурсу.
IVконкурс: Финиш.
1. Площадь прямоугольника равна 313,6 см2, одна из его сторон в 6,4 короче другой. Найдите периметр прямоугольника.
2. Основание равнобедренного треугольника равно 8см, а угол при основании 150. Найдите площадь треугольника.
Подведение итогов по конкурсу.
Заключительное слово учителя. Анализ урока.
К уроку были разработаны:
Рефлексия
Таблица подведения итого конкурсов.
Конкурсы
I команда
II команда
презентация
разминка
старт
забег
финиш
итого
Оценочные листы:
Групповой оценочный лист.
№
Фамилия, имя ученика
разминка
старт
забег
финиш
итого
1
2
3
4
5
6
Индивидуальный оценочный лист для группы поддержки.
Оценочный лист ______________ (Фамилия, имя ученика)
наименование
баллы
итого
разминка
старт
забег
финиш
Решения к уроку.
Решение задач:
-
Разминка:
Дано: ABCD - параллелограмм
AB=7см, AD=12см, BH=?
Найти: S-?
Решение: S=BH![]() AD
AD
найдем высоту BH, катет, лежащий против угла в 300 равен половине гипотенузы. BH =![]() АВ, BH=7
АВ, BH=7![]() = 3,5. S= 3,5
= 3,5. S= 3,5![]() 12=42 см2
12=42 см2
-
Старт:
1.Дано: с=13см, ![]() =350,
=350,
Найти: а, b,![]()
Решение: ![]() ; а =
; а = ![]() 13
13![]() 0,5736=7,46;
0,5736=7,46;
![]() 900 - 350 = 550;
900 - 350 = 550;
![]() b2 = с2 - а2 = 132 - 7,462 = 113,35;
b2 = с2 - а2 = 132 - 7,462 = 113,35;
b=![]() =10,65.
=10,65.
2. Дано: ABCD - параллелограмм
BD =10см -диагональ.
P![]() ABD = P
ABD = P![]() BCD = 36см,
BCD = 36см,
Найти: Р -? Параллелограмма
Решение: BD-общая сторона для двух треугольников,
P![]() ABD = AB+AD+BD,
ABD = AB+AD+BD,
36 = (AB+AD) + 10;
AB+AD = 36-10 = 20см,
P = 2![]() (AB+AD) = 20
(AB+AD) = 20![]() =40см.
=40см.
-
Забег:
-
S =
 BC
BC CA
CA 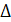 =
= 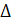 8
8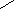 9
9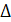 =18 см2
=18 см2 -
АС2 = 132 - 122 = 52, по теореме Пифагора АС=5, S =
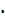 =30 см2
=30 см2 -
S =
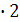 =
=  ;
; -
S =
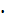 =
= 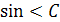 = 84см2 по формуле Герона S =
= 84см2 по формуле Герона S = 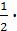 ;
; -
S = BH
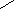 AD; BH = 10
AD; BH = 10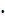 = 10
= 10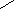 0,8660 = 8,66; S = 15
0,8660 = 8,66; S = 15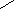 8,66 = 129,9 см2
8,66 = 129,9 см2 -
S =
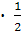 =
= 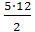 = 20см2;
= 20см2; -
По условию: AB II FE, по теореме Фалеса CK II AB II FE, FD = 2см, KF = 2см, KD = 4см, AD = 3+4 = 7см;
S = ![]() =
= ![]() = 25см2
= 25см2
---------------------------------------------------------------
Для группы поддержки:
1) S = ![]() см2; 2) S = 14
см2; 2) S = 14![]() 10 =140 см2; 3) S =
10 =140 см2; 3) S = ![]() = 56см2;
= 56см2;
B
b
a
C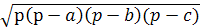 Финиш:
Финиш:
-
D
AДано: ABCD-прямоугольник
S =313,6 см2
b-?, a - 6,4b.
Найти: P-?
Решение: S = a![]() b,
b,
313,6 = 6,4b2
b2 = 313,6:6,4 = 49
b =![]() = 7, a = 7
= 7, a = 7![]() 6,4 = 44,8
6,4 = 44,8
ВP = 2![]() (a +b) =2
(a +b) =2![]() (7+44,8) = 103,6
(7+44,8) = 103,6
-
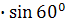 Дано :
Дано : 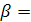 АВС-равнобедренный.
АВС-равнобедренный.
АС - 8см,
![]() = 150
= 150
Найти: S![]() ABC = ?
ABC = ?
Р
Н
С
Аешение: S = ![]() AC
AC![]() BH,
BH,
BH = tg 150![]() AH,
AH,
AH = 4см по свойству равнобедренного треугольника равна
ВН = 4![]() 0,2679 = 1,07
0,2679 = 1,07
S = ![]() 8
8![]() 1,07 = 4,28 см2
1,07 = 4,28 см2