- Учителю
- Урок математика 6 класс
Урок математика 6 класс

Обобщающее повторение темы:
« Делимость натуральных чисел»
Цели урока:
1. Образовательные: повторение, обобщение и проверка знаний по теме: « Делимость натуральных чисел »; выработка основных навыков.
2. Развивающие: развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
3. Воспитательные: посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.
Задачи урока:
Формировать умения применять понятие делителей и кратных; развивать мышление и элементы творческой деятельности; применять признаки делимости в простейших ситуациях; нахождение НОД и НОК чисел, развивать наблюдательность и логическое мышление.
Тип урока - комбинированный.
Форма урока - урок с компьютерной поддержкой.
Оборудование: 1. Доска и мел.
2. Компьютер и проектор.
3. Бумажный вариант всех заданий.
Ход урока.
Числа правят миром.
Пифагор.
-
Организационный момент.
-
Сообщение цели урока. ( слайд 1)
-
Актуализация опорных знаний. ( слайд 2) 1. Что называется делителем числа а?
2. Что называется кратным числа а?
3. Существует ли наибольшее кратное число?
4. Сформулировать признаки делимости?
5. Какие числа называются простыми, а какие составными?
( Сообщение учащихся о Пифагоре, о Эратосфене, о Евклиде)
Исторические сведения:
-
Евклид - древнегреческий ученый (365 - 300 г до н.э). О жизни этого великого ученого известно очень мало. Он жил и трудился в Александрии, городе, основанном Александром Македонским. С именем Евклида связано много легенд. Одна из них рассказывает, что царь Птолемей спросил Евклида : « Нет ли более короткого пути к познанию геометрии?», - на что ученый ответил: « Нет царской дороги в геометрию!». Евклид много занимался теорией чисел: именно он доказал, что простых чисел бесконечно много. Алгоритм нахождения НОД двух чисел, называется алгоритмом Евклида.
Древнегреческий математик Евклид в свой книге « Начала», которая была на протяжении двух тысяч лет основным учебником математики, доказал, что простых чисел бесконечно много, т.е. за каждым простым числом есть еще более простое число.
Пифагор (6 век до н.э.) и его ученики изучили вопрос о делимости чисел. Число равное сумме всех его делителей ( без самого числа ) , они назвали совершенным числом.
Например число 6 ( 6 = 1 + 2 + 3 ) , 28 ( 28 = 1 + 2 + 4 + 7 + 14 ) совершенные.
Следующие совершенные числа 496, 8128, 33550336
Пифагорейцы знали только первые три совершенных числа. Четвертое 8128 стало известно в І веке до н.э.
Пятое число 33550336 было найдено в 15 веке.
К 1983 г. Было известно уже 27 совершенных чисел. Но до сих пор ученые не знают, есть ли нечетное совершенное число, есть ли самое большое совершенное число. Интерес древних математиков к простым числам связан с тем, что любое натуральное число, больше 1 , либо простое число, либо может быть составлено в виде произведения простых чисел: 14 = 2∙ 7, 16 = 2∙2 ∙2∙2
Возникает вопрос: существует ли последнее (самое большое) простое число?
Задача: Задумано простое число. Следующее за ним натуральное число тоже простое. О каких числах идет речь?
Ответ : 2,3.
6. Какие числа называются взаимно простыми?
7. Объяснить, как найти НОД ( НОК) двух чисел.
( Сообщение учащегося о нахождении НОД двух чисел)
Однажды числа 24 и 60 поспорили о том, как им найти НОД. Число 24 утверждало, что сначала надо найти среди всех делителей общие числа, а потом выбрать из них наибольшее число. А число 60 возражало:
- Ну что ты! Мне такой способ не нравится. У меня слишком много делителей, и при их перечислении я могу пропустить какой-нибудь. А вдруг он окажется наибольшим? Нет мне такой способ не нравится. И решили они обратиться за помощью к магистру ДЕЛЕНЧЕСКИХ наук. И магистр им ответил:
- Да 24, твой способ нахождения НОД чисел можно использовать, но это не всегда удобно. А можно найти НОД по-другому.
Нужно 24 и 60 разложить на простые множители .
24
2
12
2
6
2
3
3
1
60
2
30
2
15
3
5
5
1
24 = 2³ ∙ 3
60 = 2² ∙ 3 ∙ 5
Нужно взять общие делители чисел с меньшим показателем степени.
НОД ( 24;60) = 2² ∙ 3 = 12.
А чтобы найти НОК двух чисел нужно:
-
Разложить на простые множители;
-
Выписать все простые множители, которые входят в первое число и во второе число с наибольшим показателем степени.
Значит:
24 = 2³ ∙ 3 60 = 2² ∙ 3 ∙ 5 НОК ( 24;60) = 2³∙ 3 ∙ 5 = 120.
-
Формирование умений и навыков учащихся.
а) работа учащихся у доски( по карточкам)
Задание №1. Спортсменов построили в колонну по 6 человек, а затем перестроили в колонну по 4 человека. Сколько всего спортсменов, если их больше 90 , но меньше 100.
Решение: НОК ( 4,6 ) = 12, значит 90 < 12х < 100, 12х = 96.
Ответ: 96 человек.
Задание №2. Число яблок в ящике меньше 200. Их можно разделить поровну между 2,3,4,5,6 детьми. Какое максимальное количество яблок может быть в ящике?
Решение: НОК ( 2,3,4,5,6) = 60. 60х < 200, значит максимальное количество в ящике 180 яблок.
Ответ: 180 яблок.
Сколько в корзине яиц, если их число одновременно делится на 2, на 3, на 5, на 10, на 15?
Решение: НОК ( 2,3,5,10,15) = 60.
Ответ: 60 яиц.
В это время работа с классом.
Задание №1. (приложение 1)

Задание №2. (приложение 2)

-
Физминутка. (приложение 3)
-
Работа с классом ( приложение 4,
приложение 5).
Задание 1 (устно)


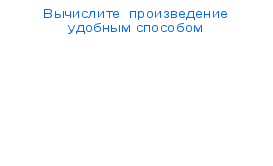
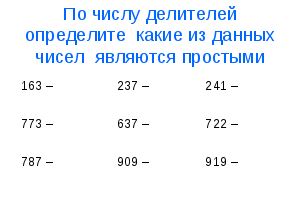
Задание 2 (письменно)

Задание 3 (письменно)
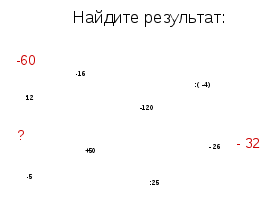
Задание 4 (письменно)

Задание 5 ( устно)


-
.Самостоятельная работа (приложение 6).

