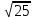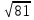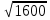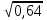- Учителю
- Конспект урока по математике 'Квадратный корень из произведения и частного' (8 класс)
Конспект урока по математике 'Квадратный корень из произведения и частного' (8 класс)
Урок № Дата
Класс 8
Тема «Квадратный корень из произведения и частного»
Цели:
-
обобщить и систематизировать знания учащихся об арифметическом квадратном корне;
-
познакомить с правилами извлечения квадратного корня из произведения и дроби;
-
отрабатывать вычислительные навыки, навыки извлечения квадратного корня;
-
развивать образное и логическое мышление, слуховую и зрительную память.
Ход урока:
-
Организационный момент.
-
Повторение.
-
Что называется арифметическим квадратным корнем из числа а?
-
При каком значении а имеет смысл выражение
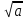 ?
? -
Из какого числа нельзя извлечь корень?
-
Назовите свойства уравнения х2=а.
-
Что представляет собой график функции у=
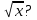
-
Сформулируйте некоторые свойства функции у=
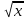 .
.
-
Устная работа.
-
Найдите значение корня:
-
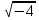
-
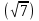 2
2
-
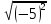
-
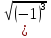 )2
)2
-
Вычислите значение выражения
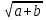 , если а=33, b=-8; a=b=98.
, если а=33, b=-8; a=b=98.
-
Изучение нового материала.
-
Откройте свои тетради и запишите тему урока: «Квадратный корень из произведения и дроби».
-
Но сначала давайте с вами поговорим об истории квадратного корня:
-
В Древней Индии неизвестное именовалось «мула», что означает «начало», «основание», «корень (дерева)». Арабы для этих целей использовали слово «джизр» с тем же значением. Европейцы перевели его на латынь как radix - «корень». Так возник математический термин «радикал». С этим названием связан и привычный нам значок корня 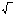 .
.
А история его такова.
На протяжении нескольких веков математики вслед за Леонардо Пизанским квадратный корень обозначали Рх(сокращение от слова radix). Постепенно Рх превратилось в строчную r. В книге по алгебре Кристофа Рудольфа - первом руководстве подобного рода, написанном на немецком языке (1525г.),- вместо r используется значок √. Этот символ уже похож на тот, которым пользуемся и мы. Современную запись корней разных степеней - 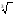 ,
,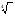 ,…- мы находим у голландского математика Альбера Жирара.
,…- мы находим у голландского математика Альбера Жирара.
А горизонтальную черту над выражением под радикалом ввёл в 1637г Рене Декарт.
-
-
Теперь приступим непосредственно к нашей теме. Для этого я предлагаю вам решить и сравнить результат:
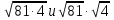 . Я попрошу решить первое выражение Валентину, а второе выражение - Сергею. Решение мы запишем и в тетрадях, и на доске.
. Я попрошу решить первое выражение Валентину, а второе выражение - Сергею. Решение мы запишем и в тетрадях, и на доске. -
К какому результату мы с вами пришли? И какой вывод можно сделать?
-
В учебнике на стр. 84 прочитайте теорему №1 и вытекающее из неё свойство
-
(Учитель записывает на доске свойство, вытекающее из теоремы.)
-
-
Выполним следующее задание:
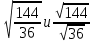 .
. -
К какому результату мы с вами пришли? И какой вывод можно сделать?
-
В учебнике на стр. 85 прочитайте теорему №2 и вытекающее из неё свойство.
-
(Учитель записывает на доске свойство, вытекающее из теоремы.)
-
Закрепление.
№ 369
a) ![]() ;
;
b) ![]() ;
;
c) ![]() ;
;
d) ![]() ;
;
e) ![]() ;
;
f) ![]()
№ 372
a) ![]() =12;
=12;
б)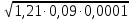 =0,0033;
=0,0033;
в) 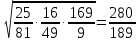 ;
;
г) 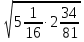 .
.
-
Самостоятельная работа (по уровням)