Обобщающий урок по теме:

"Производная и ее геометрический смысл"

Цели урока:

• Образовательные: обобщить и систематизировать знаний учащихся по данной теме: выработать умения нахождения производной, применения правил дифференцирования, составления уравнений касательной к графику функции в заданной точке; подготовка к ЕГЭ

• Развивающие: развитие математической речи, логического мышления, сообразительности, внимательности.

• Воспитательные: воспитание трудолюбия, аккуратности.

• Оборудование: раздаточный материал с тестовыми заданиями,

• компьютерная презентация (PowerPoint),.

В ходе создания использовались следующие программные средства:

• Microsoft Word - набор и редактирование текста;

• Microsoft PowerPoint - создание презентации.

План урока

1. Организационный этап. Постановка цели.

2. Проверка домашнего задания..

3. Устные упражнения

4. Самостоятельная работа в форме теста

5. Решение задач из КИМов

6. Письменные тренировочные упражнения

7. Итог урока, выставление оценок

8. Сообщение домашнего задания.

Ход урока.

1. Организационный этап. Постановка цели урока

Цель урока - обобщить, систематизировать изученный материал по теме "Производная и её геометрический смысл" Подготовиться к контрольной работе и к ЕГЭ

2. Проверка домашнего задания

№122 . №123 (два ученика выполняют на доске эти задания, а остальные выполняют устную работу)

III Устная работа

Опрос теории

1. Что называется производной функции f(x) в точке х?

2. В чем состоит геометрический смысл производной?

3.Сформулировать правила дифференцирования суммы, произведения, частного

4. Запишите уравнение касательной.

(После фронтального устного опроса проверяется работа учеников, работающих у доски)

Устные упражнения

.Найдите производную функций

См. рис. Что можно сказать о касательной к графику функции?

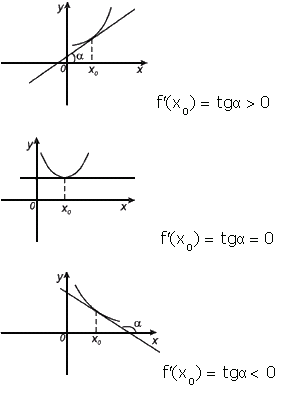
Устно: 1. Какое значение принимает производная функций y=f(x) в точке А?

y

А • y=f(x)

0 1

2.Какое значение принимает производная функции в точке В?

у

B •

1 y=f(x)

0 х

IV. Самостоятельная работа в форме теста

Учащимся необходимо выбрать правильный ответ.

. Найдите значение производной функции у=х²е^х в точке х₀=1.

. Найдите значение производной функции у = еlnх в точке х₀=1

е

0

1

3е

Решение проверяется через проектор.

Вариант 1 Вариант 21. На рисунке изображены график функции у= f(x) и касательная к этому графику, проведенная в точке с абсциссой х_о. Найдите значение производной в точке х_о

№2 На рисунке изображены график функции у= f(x) и касательная к этому графику, проведенная в точке с абсциссой хо. Найдите значение производной в точке хо

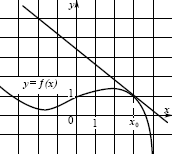
3. На рисунке изображены график функции у= f(x) и касательная к этому графику, проведенная в точке с абсциссой хо. Найдите значение производной в точке хо

№4. К графику функции y = f(x) в его точке с абсциссой х₀ = -3 проведена касательная. Определите угловой коэффициент касательной, если на рисунке изображен график производной этой функции.

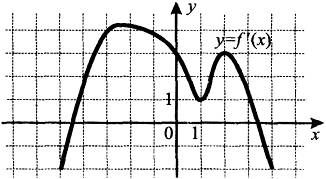
№5. На рисунке изображен график производной y= f'(x) функции f(x)

определенной на интервале (-3;3). Укажите абсциссу точки, в которой

касательная к графику функции y=f(x) параллельна прямой у=4+х или

совпадает с ней

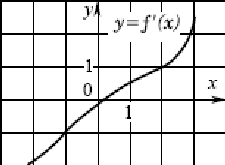
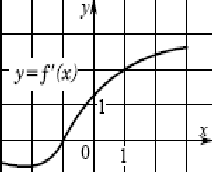
№6 На рисунке изображен график производной y= f'(x) функции f(x)

определенной на интервале (-3;3). Укажите абсциссу точки, в которой

касательная к графику функции y=f(x) параллельна прямой у=2х или

совпадает с ней.

VI Письменные тренировочные задания

Задача №1

Напишите уравнение касательной, проведенной к графику функции

через точку с абсциссой х = 3

Решение: Запишем уравнение касательной у = f(x ) + f(x ) (x-x ).

F(3) = 9+6 = 15 - ордината точки касания, f xx + 2, f (3) = 8 - угловой

коэффициент касательной. Подставим полученные значения в уравнение

касательной. Получим у = 15 + 8(х - 3), у = 8х - 9 - уравнение касательной

Задача №2

Написать уравнение касательной к графику функции f(х) = Sin 2x - ln (х+1)

в точке с абсциссой х=0

Задача №3

Найдите ошибку, если она есть

.

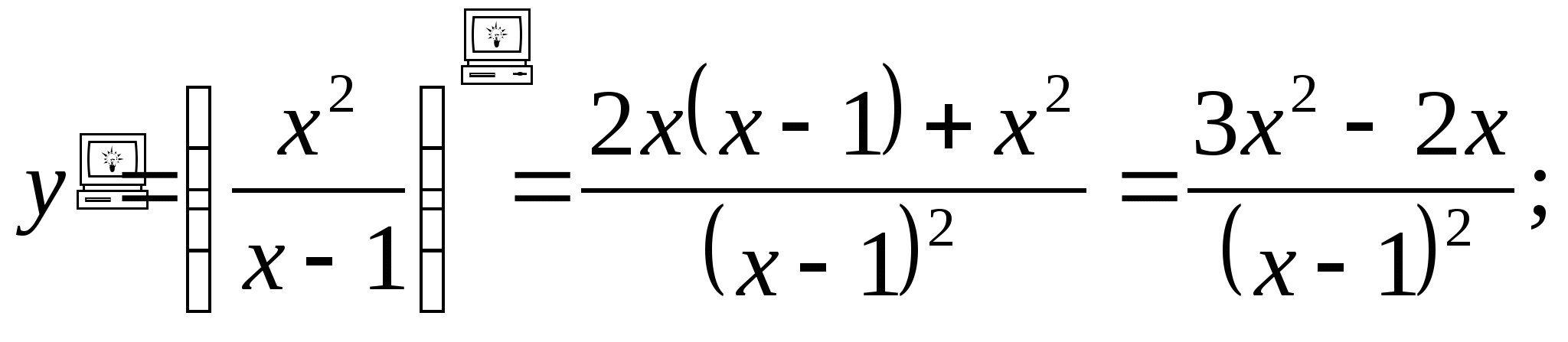
VII. Подведение итогов урока

Закончите фразу:

• «Сегодня на уроке я повторил …»

• «Сегодня на уроке я научился…»

VIII. Домашнее задание

• Стр.95. Повторить вопросы к главе II

• Стр.96. Упр. «Проверь себя»

• Подготовиться к контрольной работе.