Конспект урока по алгебре на тему 'Уравнения' (9 класс)

МКОУ Ударниковская ООШ

Урок по алгебре в 9 классе

Тема урока:

Повторение и обобщение темы «Уравнения»

Цели урока:

• Повторить, систематизировать и закрепить знания об уравнениях и способах их решений.

• Способствовать выработке навыка решения уравнений.

• Развивать логическое мышление учащихся.

• Воспитывать трудолюбие, ответственность при подготовке к экзаменам по алгебре.

Подготовка к уроку:

обобщающие таблицы по теме «Уравнения», карточки к тестированию по теме «Арифметическая и геометрическая прогрессии»,

сборник задач к экзамену

Учитель: Диденко В.Е.

1.Сообщение целей урока и этапов проведения.

2.Тестирование по теме: «Арифметическая и геометрическая прогрессии»

3.Повторение темы «Уравнения»

• Линейные уравнения.

• Квадратные уравнения.

• Дробно рациональные уравнения.

• Уравнения 3-й и выше степеней (в том числе биквадратные уравнения).

• Уравнения, содержащие знак модуля.

• Уравнения с параметром.

Уравнение- равенство, содержащее переменную

Корень уравнения - значение переменной, при котором уравнение обращается в верное равенство.

Решить уравнение - значит найти все его корни или доказать, что корней нет.

1. Линейные уравнения. 3 ученика у доски решают уравнения

1ученик 2ученик 3ученик

2 - 3(х+2) = 5 - 2х 2х+5 = 2х + 12 3( х + 2) + х = 6 + 4х

х = -9, 0х =7, 0х = 0,

уравнение имеет уравнение не имеет уравнение имеет

1. корень корней бесчисл. множество корней

Уравнения вида ах = b, где х -переменная, а, b - некоторые числа называется линейным уравнением с одной переменной.

2. Квадратные уравнения. 3 ученика у доски решают уравнения

1ученик 2ученик 3ученик

-10х² - 9х + 1 = 0 3х² - 2х - 1 = 0 х ²- 2х + 4 = 0

формула 1 формула 2 формула 2

уравнение имеет уравнение имеет уравнение не имеет

2. корня 1корень корней

Уравнение вида ах² +bх + с = 0, где х - переменная, а,b,с - некоторые числа( а= 0) называется квадратным уравнением.

D = b² - 4ac - дискриминант квадратного уравнения

Неполные квадратные уравнения( ах² + bх = 0, ах ²+ с = 0, ах² = 0)

Решить самостоятельно: 3х² - 2 = 0, (х₁ =0, х₂=2/3 ); 7х² - 14 = 0,(х₁=2,х₂=-2)

Приведенное квадратное уравнение - уравнение в котором а = 1.

Теорема Виета

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

х₁ + х₂= -p и х₁ х₂ = q

3. Дробно - рациональные уравнения.

Уравнение с переменной в знаменателе ( уравнение вида P(х)/Q(х) =0) называется дробно рациональным уравнением.

Алгоритм решения: 1. найти общий знаменатель дробей, входящих в уравнение;

2.умножить обе части уравнения на общий знаменатель;

3.решить получившееся целое уравнение;

4.исключить из его корней те, которые обращают в нуль общий знам-ль.

Решить уравнение:

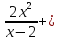
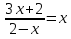2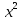-3x-2=x²(x-2)

(x-2)(2x+1)= x²(x-2)

x²(x-2) - (x-2)(2x+1)=0

(x-2)( x² - 2x-1)=0

x-2= 0 или x² - 2x-1=0

X=2 x= 1-, x= 1+,

X=2 - не является корнем уравнения

Ответ: 1-, 1+,

4. Уравнения 3-й и выше степеней.

Приемы решения:

• метод разложения на множители(вынесение за скобки, способ группировки),

• графический метод,

• метод введения новой переменной( биквадратные уравнения, ах⁴+bx²+c=0).

Найти метод решения уравнений (уравнение на экране через кодоскоп)

Решить биквадратное уравнение: 9х ⁴- 10х² + 1 =0, (х₁=1, х₂=-1, х₃=1/3, х₄= -1/3)

Решить уравнение: х³ - 3х² - 32х + 96 = 0, ( х₁ = 3, х₂ = 4 2, х₃ = -4 2)

Подведение итогов урока

Основные группы уравнений: линейные

квадратные

дробно - рациональные

уравнения высших степеней

Основные приемы решений уравнений: по формулам

разложение на множители

введение новой переменной

равенство дроби 0

Домашнее задание: алгебра 9 кл. п.12,13, стр.245-246, повторить «Уравнения»- алгебра 7кл.,8кл.

Сб. к экзамену - выбрать и решить различные виды уравнений

Контроль знаний и умений по теме: «Прогрессии»

1. Заполни таблицу

Арифметическая

прогрессия

Геометрическая

прогрессия

Определение

Рекуррентная

формула

Разность прогрессии

Знаменатель прогрессии

Формула n-го члена

Сумма n - первых

Членов

Сумма бесконечной прогрессии

Характеристическое

Свойство