конспект о радианной мере угла 10 класс

Градусная и радианная мера угла. Тригонометрический круг

Гусная и ная мера угла. Тригонометрический круг

Если угол содержит α° и одновременно измеряется x , то , где K° - постоянный коэффициент. Подставляя, например, и , получаем 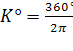. Наоборот, , где .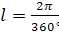

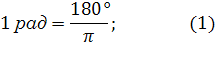
Пример 1. Выразим в ной мере величины углов в 90°, 45°, 60° и 27°.

Решение. з формулы (2) следует: .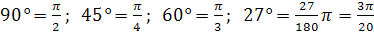

Пример 2. Выразим в гусной мере величины углов в .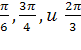

Решение. з формулы (2) следует: .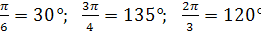

Поворот точки вокруг начала координат

Рассмотрим на координатной плоскости окружность иуса 1 с центром в начале координат. Ее называют единичной окружностью. Введем понятие поворота точки единичной окружности во круг начала координат на угол α , где α - любое действительное число.

1. 1. Пусть α>0. Предположим, что точка, двигаясь поединичной окружности от точки Р против овой стрелки, прошла путь длиной α (рис. 1). Конечную точку пути обозначим М.

В ом случае будем говорить, что точка М получена из точки Р поворотом вокруг начала координат на угол α .

2. 2. Пусть α<0. В ом случае поворот на угол α означает, что движение совершалось по овой стрелке и точка прошла путь длинной (рис. 2).

Поворот на 0 означает, что точка остается на месте.

Примеры.

1) При повороте точки Р(1;0) на угол (рис. 3) получается точка М с координатами (0;1).

2) При повороте точки Р(1;0) на угол (рис. 3) получается точка N(0;-1).

3) При повороте точки Р(1;0) на угол (рис. 4) получается точка К(0;-1).

4) При повороте точки Р(1;0) на угол (рис. 4) получается точка Д(-1;0).

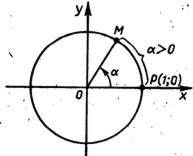
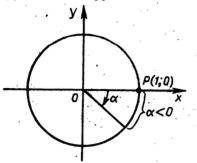
Рис. 1

Рис. 2

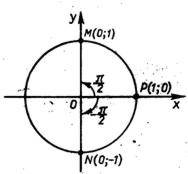
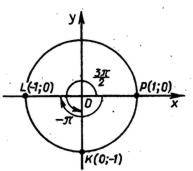
Рис. 3

Рис. 4

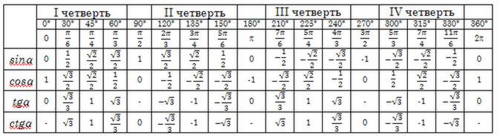
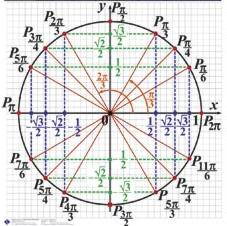
Приведем таблицу поворотов на некоторые углы, выраженные в ной и гусной мерах (рис. 5).

Отметим, что при повороте точки Р(1;0) на 2, т.е. на 360°, точка возвращается на первоначальное положение (см. таблицу). При повороте точки на -2, т.е. на -360°, она также возвращается в первоначальное положение.

Рассмотрим примеры поворотов точки на угол, больший 2, и на угол, меньший -2. Так, при повороте на угол точка совершает два полных оборота против овой стрелки и проходит еще путь (рис. 6). При повороте на угол точка совершает два полных оборота по овой стрелке и проходит еще путь в том же направлении (рис. 7).

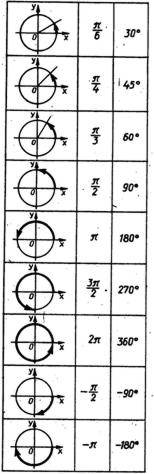
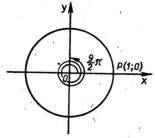
Рис. 6

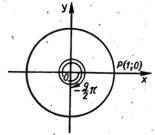
Рис. 5

Рис. 7

Свойства тригонометрических функций

Знаки тригонометрических функций

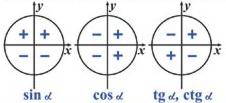
Свойство четности и нечетности

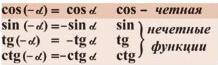
Свойство периодичности

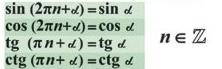
и

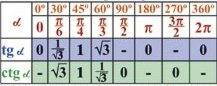
Значения tg и ctg угла α

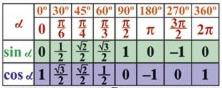
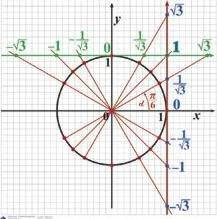
Значения и cos угла α

- это угол поворота, при котором конец начального иуса осывает дугу, длина которой равна иусу.