Конспект урока по математике на тему «Длина окружности» (6 класс)

2. Создание проблемной ситуации

Учитель. На уроке необычные гости. Давайте поинтересуемся, как они здесь появились?

Баба Яга. Как появились? Эх, ступа повредилась. Придется к лешему в ремонт тащить.

Ученик. Не успел и глазом моргнуть, а Баба Яга тут как тут.

Баба Яга. Починил, лохматый? Только сдается мне, скорость у неё не та стала. Как бы проверить?

Ученик. Очень просто. Ты полетай по кругу. Я время замечу, а скорость вычислим по формуле .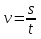

Баба Яга. Как же мой путь измерить? Он же не прямой!

Ученик. Эх, ты ещё древние греки умели находить длину окружности по формуле С=d, где d- диаметр окружности.

Баба Яга. Это что за «закорючка» в формуле?

Ученик. Это греческая буква «Пи».

Учитель. Как же ребята найти это число 

3. Практическая работа

(Выполняется в парах; учащиеся приносят на урок банки)

Учитель. Если «опоясать» банку ниткой, а затем её «Распрямить», то длина нитки будет приблизительно равна длине окружности банки. Чтобы получить более точный результат, нужно «опоясать» банку ниткой несколько раз, а затем длину всей нити разделить на количество «опоясывающих» кругов. Затем нужно измерить диаметр окружности банки линейкой и из формулы С=d найти неизвестный множитель , т.е. разделить длину окружности на диаметр.

Ученики используют микрокалькулятор, округляя значения до сотых. Полученные данные заносят в таблицу, которая имеется на каждой парте.

С₁

С₂

С₃

С_ср

d



Данные учащихся обобщаются в таблице

Значение 

1-й ряд

2-й ряд

3-й ряд

Среднее арифметическое

Если измерения и вычисления выполнены аккуратно, то получаем значение , равное 3,1-3,2. Так как d=2r, то получаем ещё одну формулу для вычисления длины окружности (через радиус): С=2r.

4. Сообщение учителя

Еще в древности людям были известны многие геометрические фигуры, в том числе окружность и круг. Об этом свидетельствуют археологические раскопки. Еще тогда приходилось решать задачи на вычисление длины окружности. Сейчас известно, что значением числа  в разные времена считали разные числа. Так в Древнем Египте(ок. 3500 лет назад) считали =3,16; древние римляне полагали, что =3,12. Все эти значения были определены опытным путем. Великий ученый Древней Греции Архимед определил, что значение p находится в следующих пределах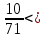: 33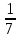. С помощью современных электронно-вычислительных машин число p было вычислено с точностью до миллиона знаков после запятой. Для обозначения частного от деления длины окружности на диаметр впервые букву  использовал английский математик Джонс в 1706 г., но общепринятым это обозначение стало благодаря работам великого математика Эйлера. Он вычислил для числа  153 десятичных знака.

5. Сообщения учащихся

1-й ученик. Число  - это бесконечная десятичная дробь. Первые восемь цифр этого числа можно запомнить так: три, четырнадцать ,пятнадцать, девяноста два и шесть (3,1415926).

Или двенадцать цифр с помощью двустишия, в котором число букв в каждом слове соответствует цифре числа :

это

я

знаю

и

помню

прекрасно

Пи-

лишние

знаки

тут

чужды,

напрасны

3

1

4

1

5

9

2

6

5

3

5

8

2-й ученик. В практических расчетах редко бывает нужно знать более трёх-пяти цифр числа . Если со временем вы их забудете, то задайте вопрос:

Что

я

знаю

о

Кругах?

3

1

4

1

5

Для закрепления в памяти рационального выражения  - числа Архимеда (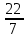) - может оказаться полезной шутка из учебника Магницкого:

Двадцать две совы скучали

На больших сухих суках.

Двадцать две совы мечтали

О семи больших мышах,

О мышах довольно юрких

В аккуратных серых шкурках.

Слюньки капали с усов

У огромных серых сов.

Учитель. Итак, длина окружности вычисляется по формуле

С=d =2r,  3,14

Баба Яга. Ага, научились, научились вычислять длину окружности! Только какой радиус нам выбрать? Подержи меня за помело, я и покручусь. В нем как раз 2 метра.

Ученик. Один оборот Баба Яга сделала за одну секунду. Помогите, ребята, найти скорость.

Учащиеся вычисляют скорость

S=C=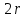=3,14*2*2= 12,56(м),

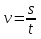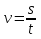= = 12,56 (м/с).

6. Решение упражнений и задач

1. Вычислите длину окружности, если r= 5 см.

()

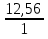2. Вычислите длину окружности, если d = 100 м.

()

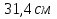3. Ученики организовали соревнования по фигурному катанию на велосипедах. В этих соревнованиях нужно было проехать четыре круга по окружности радиусом 3м. Какое расстояние проехали велосипедисты в этом виде фигурного катания?

(75м)

7. Подведение итогов урока. Задание на дом

Литература

1. Математика.6 класс : учеб. для учащихся общеобразовательных учреждений / И.И. Зубарева, А.Г.Мордкович. - 13-е изд., испр. и доп. - М. : Мнемозина, 2013. -264 с.: ил.

2. Арутюнян Е.Б., Левитас Г.Г. Сказки по математике.- М., 1994.

3. Эмоциональная презентация детище несоизмеримости.- М., Математика в школе, №1/ 1998.