Конспект урока по геометрии в 11-м классе на тему «Простейшие задачи в координатах».

Конспект урока по геометрии в 11-м классе на тему

«Простейшие задачи в координатах».

Цели урока:

Образовательные: научится решать задачи с использованием системы координат: нахождение координат середины отрезка; определение длины вектора; определение расстояния между точками. Подготовится к решению задач с использованием метода координат.

Воспитательные:

Развивающие: способствовать развитию навыков применения формул для вычисления длины вектора и нахождения координат середины отрезка при решении задач

Тип урока: сообщение нового материала.

Вид урока: комбинированный.

Демонстрация: презентация с решением простейших задач в координатах.

Оборудование: компьютер, мультимедийный проектор, интерактивная доска.

Структура урока:

1. Организационный момент;

2. Сообщение темы урока;

3. Изучение и объяснение нового материала;

4. Закрепление материала, изученного на данном уроке;

5. Подведение итогов и результатов урока;

6. Задание на дом.

Литература:

1. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. Геометрия, 10 - 11: Учебник для общеобразовательных учреждений, - М.: Просвещение, 2010г. - 255с.

План урока:

Ход урока.

1. Организационный момент.

2. Сообщение темы урока. (Слайд 1)

3. Изучение нового материала.

Задача № 1. Связь между координатами векторов и координатами точек.

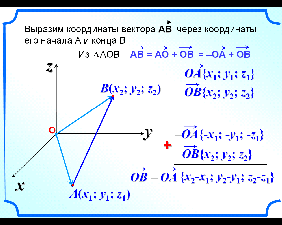На интерактивной доске, появляется слайд 2, на котором изображен век­тор в ПСК. И требуется выразить координаты этого вектора через ко­ординаты его начала и конца. Прово­дим радиус-векторы и .

Раскладываем вектор по векторам и .

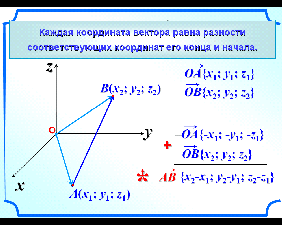
Приходим к выводу (слайд 3), что ка­ждая координата вектора равна разности соответствующих коорди­нат его конца и начала. Учащиеся к себе в тетрадь записывают оконча­тельную формулу:

Задача № 2. Координаты середины отрезка.

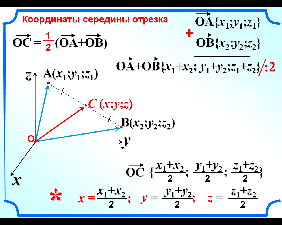
В системе координат отметим точку с координатами и точку с координатами (слайд 4). Выразим коорди­наты середины отрезка через координаты его концов.

Так как точка середина отрезка , то . Координаты векторов и равны соответствующим координатам точек и : и .

Сложив координаты векторов и и разделив на 2, получаем коорди­наты

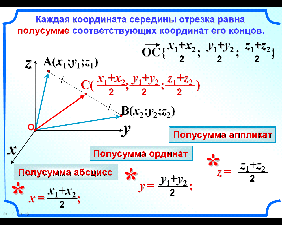вектора (Слайд 5).

Вывод: каждая коорди­ната середины отрезка равна полу­сумме соответствующих координат его концов.

Запись в тетрадь:

Задача № 3. Вычисление длины вектора по его координатам.

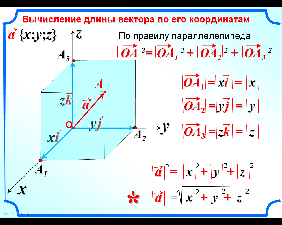На слайде 6 в ПСК задан вектор . Требуется вычислить длину этого вектора.

Отложим на осях координат векторы , , и рассмотрим вектор .

По правилу параллелепипеда: .

Тогда длина вектора равна: .

Так как , , и , то получаем .

Следовательно .

Записать полученную формулу в тетрадь.

Задача № 4. Расстояние между двумя точками.

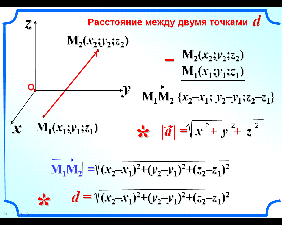Рассмотрим две произвольные точки: точку с координатами и точку с координатами (слайд 7). Выразим расстояние между точками и через их координаты.

С этой целью рассмотрим вектор . Его координаты равны . Длина этого вектора будет равна (вычисляется по формуле, рассмотренной в предыдущей задаче: ) . Причем

Вывод: расстояние между точками и вычисляется по формуле (записать в тетрадь).

4. Закрепление изученного материала.

На интерактивной доске, появляются слайды с заданиями для закрепления изученного материала. Сначала учитель показывает и еще раз проговаривает каждый этап решения, затем вызывает к доске ученика.

2. Найти координаты середины отрезка.

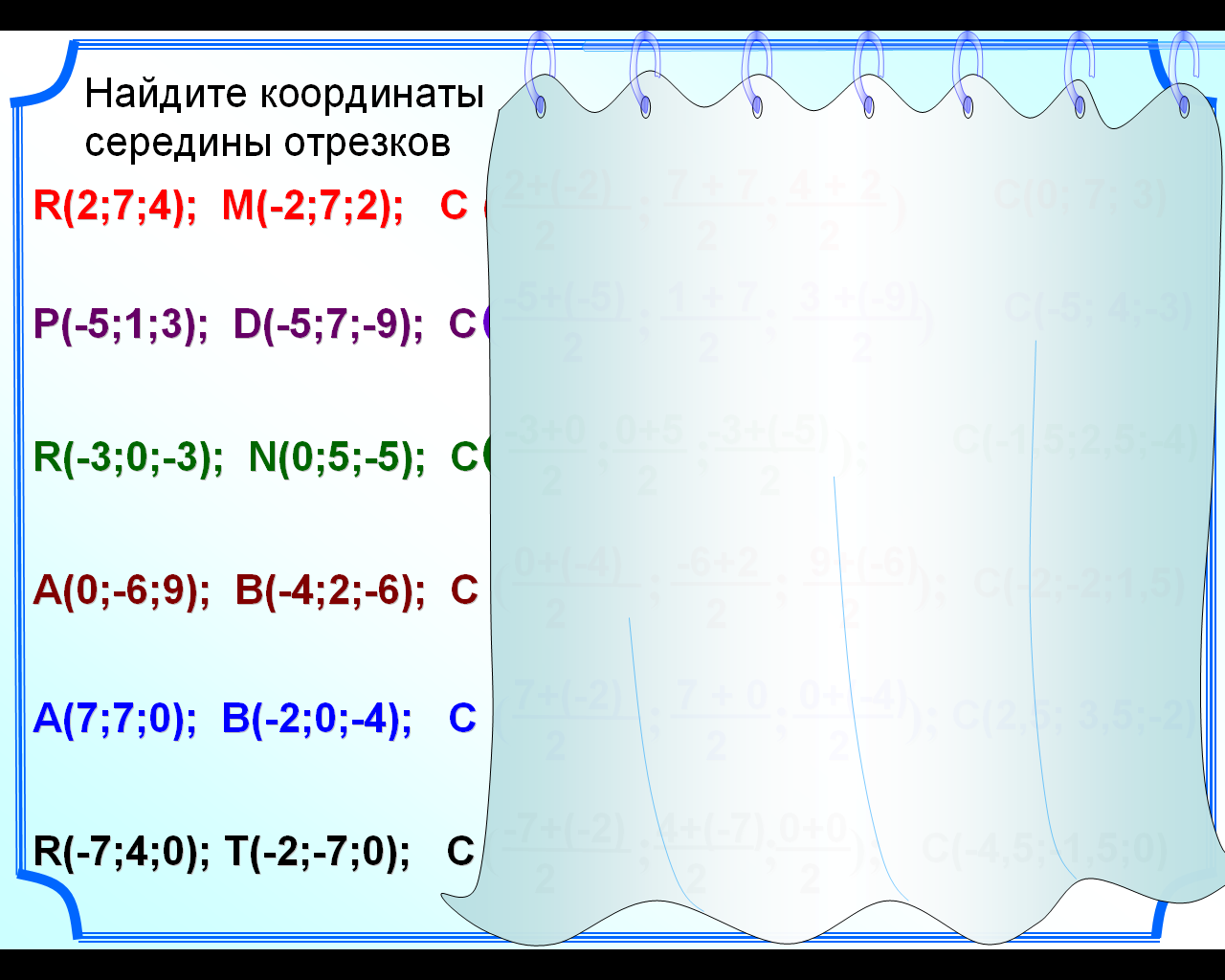
3. Найти длину вектора.

5. Подведение итогов урока.

6. Домашнее задание

§ 44 - 45, № 417, 418.

Учитель математики: Кондратьев И. В.

____________________________________________