- Учителю
- Структурно-логические таблицы по геометрии 10 класс
Структурно-логические таблицы по геометрии 10 класс




















 Анализ:
Анализ:
1.данных
2.чертежа
3.определений
4.теорем и их
следствий
Влияющие факторы:
-
Исходные данные
-
Чертеж
-
способы решения
Перпендикулярность в пространстве
Перпендикулярные прямые:
 Свойство:
Свойство: 
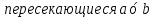
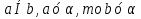 Если
Если 
Перпендикулярность прямой и плоскости:
Определение Признак
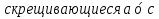 перпендикулярности прямой и плоскости
перпендикулярности прямой и плоскости
Перпендикулярность плоскостей:
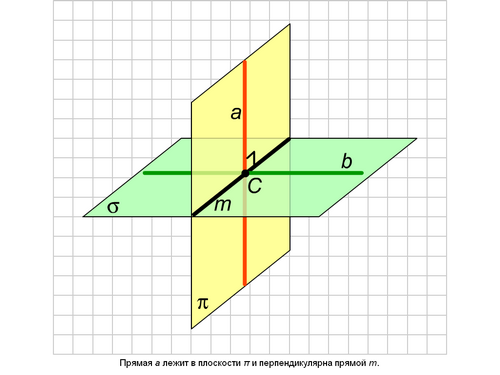
Проблемы:
1.построение чертежа
2. решение задач по стереометрии
3. развитие логического мышления
4.развитие пространствен-
ного воображе-
ния
Опыт. Практика
1.решение стереометрических задач.
2. подготовка к ЕНТ
3. Межпредметные связи:
а) в черчении;
б) в физике;
в) в строительстве;
г) в архитектуре
Анализ: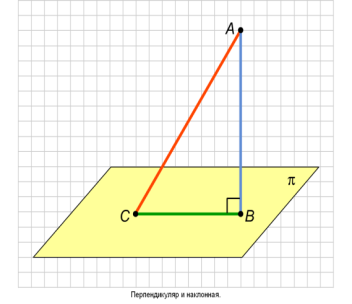
1.данных
2. чертежа
3.определений
4. теорем и их следствий
Влияющие факторы:
-
Исходные данные
-
Чертеж
-
Способы решения
Перпендикуляр и наклонная
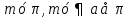 B
B
АС=AD,
то CB=BD
АВ , AC-наклонная, СВ- проекция АС на
, AC-наклонная, СВ- проекция АС на 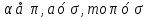
Теорема о трех перпендикулярах
Прямая: 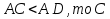
Обратная: AH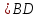
Расстояние
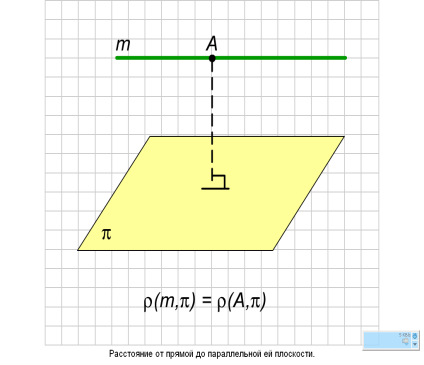
между прямой и параллельной ей плоскостью
между скрещивающими прямыми
от точки до плоскости
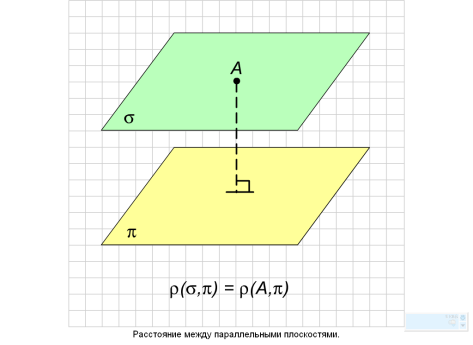
между параллельными плоскостями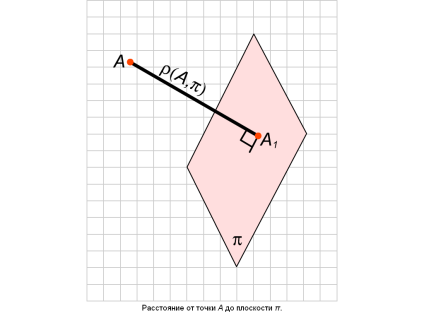

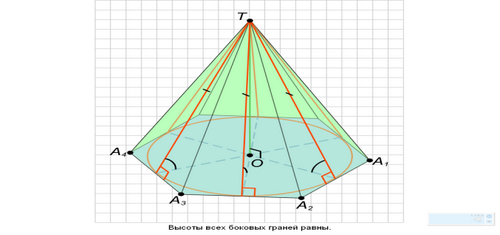
Свойство точки, равноудаленной
TH1= TH2= TH3=… =THn , то Н»O=Н2O=Н3O=…=НbO=r
=
…
SA1= SA2= SA3=…= SAn , то A1O= A2O= A3O=…= AnO=Rот вершин многоугольника от сторон многоугольника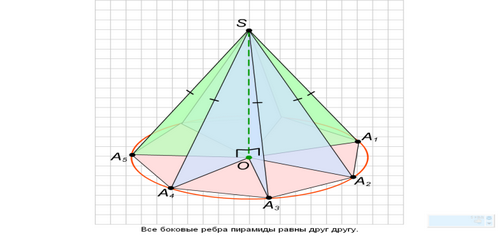
Проблемы:
1.построение чертежа
2. решение задач по стереометрии
3. развитие логического мышления
4.развитие пространствен-
ного воображе-
ния
Опыт. Практика
1.решение стереометрических задач.
2. подготовка к ЕНТ
3. Межпредметные связи:
а) в черчении;
б) в физике;
в) в строительстве;
г) в архитектуре;
д) в технике.
Анализ:
1.данных
2. чертежа
3.определений
4. теорем и их следствий
Влияющие факторы:
-
Исходные данные
-
Чертеж
-
Способы решения
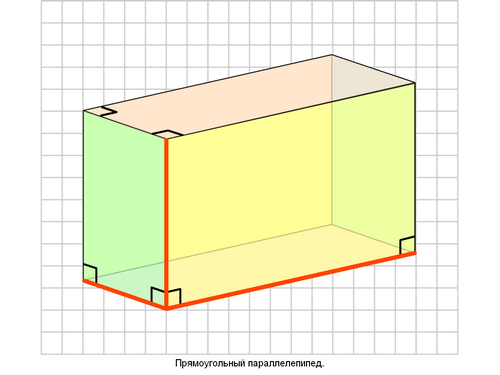
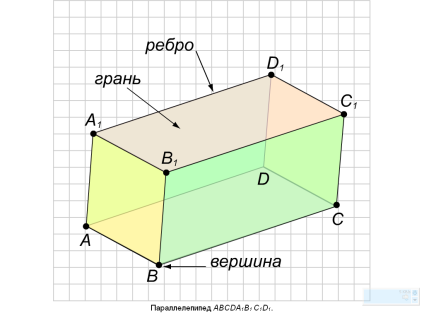
АС1-прямоугольный параллелепипед
ABCD, A1B1C1D1 - основания
AA1, BB1, CC1, DD1- боковые ребра (с)
AA1B1B=CC1D1D, BB1C1C=AA1D1D- боковые грани
BD1=AC1=B1D=A1C-диагонали параллелепипеда (d)
BD- диагональ основания
AB1 -диагональ боковой грани
BB1D1D, AA1C1C- диагональное сечение (прямоугольник)
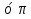 -угол наклона диагонали к плоскости основания
-угол наклона диагонали к плоскости основания
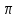
угол наклона диагонали к боковой граниПрямоугольный параллелепипед и его элементы
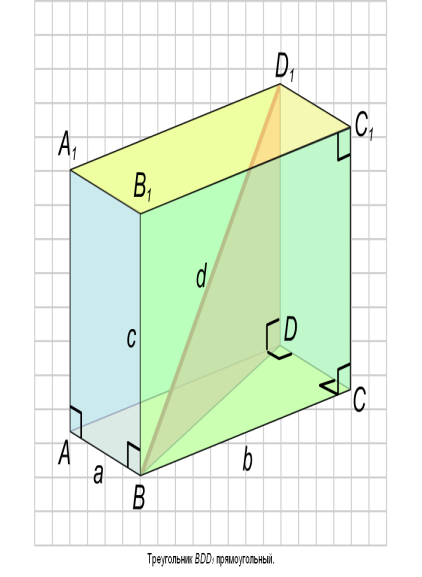
Диагональ прямоугольного параллелепипеда:

Площадь боковой и полной поверхности:
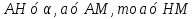
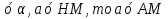
Площадь диагонального сечения:
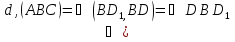
Объем: 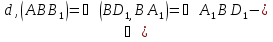
Угол наклона диагонали к плоскости:
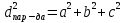 ,
, 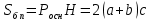
Проблемы:
1.построение чертежа
2. решение задач по стереометрии
3. развитие логического мышления
4.развитие пространствен-
ного воображе-
ния
Опыт. Практика
1.решение стереометрических задач.
2. подготовка к ЕНТ
3. Межпредметные связи:
а) в черчении;
б) в физике;
в) в строительстве;
г) в архитектуре;
д) в технике
е) при ремонте квартиры
Анализ:
1.данных
2. чертежа
3.определений
4. теорем и их следствий
Влияющие факторы:
-
Исходные данные
-
Чертеж
-
Способы решения
КУБ
Sб.п. =4а2 Sп.п.=6а2
V=a3
a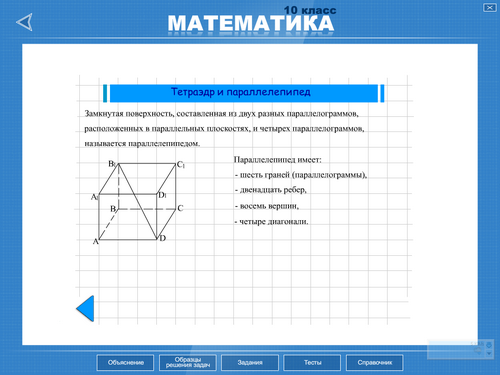
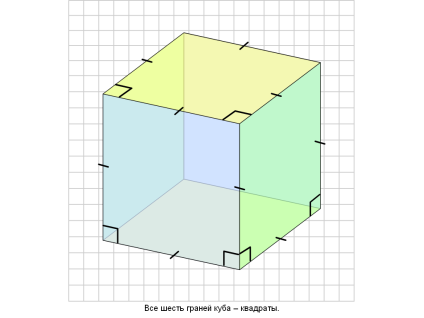
АBCD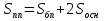 -куб (все грани равные квадраты площадью
-куб (все грани равные квадраты площадью 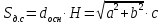 )
)
ABCD, A1B1C1D1 - основания
AA1, BB1, CC1, DD1- боковые ребра (а)
AA1B1B=CC1D1D=BB1C1C=AA1D1D- боковые грани BD1=AC1=B1D=A1C-диагонали параллелепипеда (d=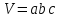 )
)
BD- диагональ основания (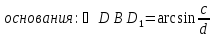 )
)
DC1 -диагональ боковой грани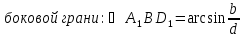 )
)
BB1D1D, AA1C1C- диагональное сечение (прямоугольник со сторонами а и а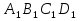 ),
), 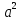
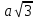
угол наклона диагонали к плоскости основания
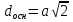
угол наклона диагонали к боковой грани
Проблемы:
1.построение чертежа
2. решение задач по стереометрии
3. развитие логического мышления
4.развитие пространствен-
ного воображе-
ния
Опыт. Практика
1.решение стереометрических задач.
2. подготовка к ЕНТ
3. Межпредметные связи:
а) в черчении;
б) в физике;
в) в строительстве;
г) в архитектуре;
д) в технике
е) при ремонте квартиры
Анализ:
1.данных
2. чертежа
3.определений
4. теорем и их следствий

Влияющие факторы:
-
Исходные данные
-
Чертеж
-
Способы решения
Углы в пространстве
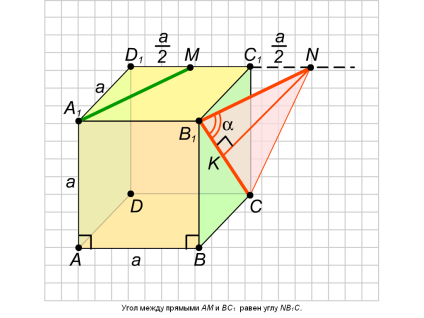
Угол между пересекающими прямыми Угол между скрещивающими прямыми
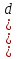
b
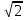
a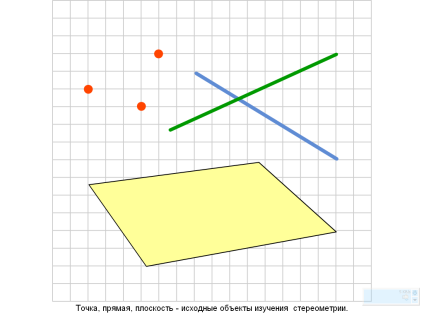

-
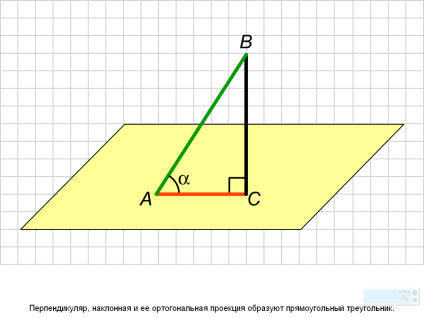
Угол между прямой и плоскостью
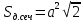 =
=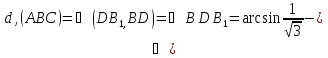 ,
,
где АВ - прямая l,
AC- ее проекция на плоскость 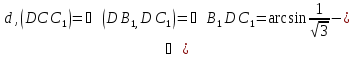 ,
,
ВС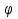

-
Угол между плоскостями
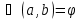 A, AB2) =
A, AB2) =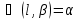 B1AB2 , где В1А
B1AB2 , где В1А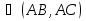 AB2
AB2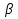
-
Площадь ортогональной проекции многоугольника
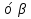 s
s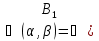 , где
, где 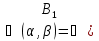 -угол между плоскостью ортогональной проекции и плоскостью многоугольника
-угол между плоскостью ортогональной проекции и плоскостью многоугольника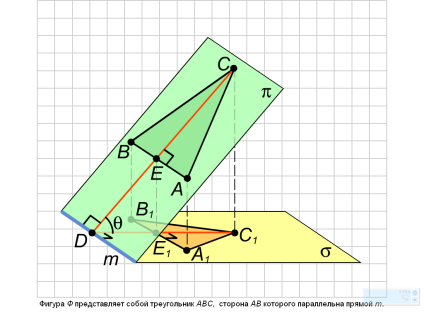

Проблемы:
а ,
, 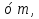 ,
, 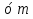 1.построение чертежа
1.построение чертежа
2. решение задач по стереометрии
3. развитие логического мышления
4.развитие пространствен-
ного воображе-
ния
Опыт. Практика
1.решение стереометрических задач.
2. подготовка к ЕНТ
3. Межпредметные связи:
а) в черчении;
б) в физике;
в) в строительстве;
г) в архитектуре;
д) в технике
е) при ремонте квартиры
Понятийный аппарат
по теме: «Перпендикулярность прямых и плоскостей»
Перпендикулярность прямых в пространстве
Определение:
Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Свойства перпендикулярных прямых:
-
Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны.
-
Если одна из двух параллельных прямых, перпендикулярна третьей, то и другая ей перпендикулярна.
Перпендикулярность прямой и плоскости
Определение прямой, перпендикулярной плоскости:
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения.
Признак перпендикулярности прямой и плоскости:
Теорема: Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.
Свойства перпендикулярных прямой и плоскости:
Теорема 1. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Теорема 2. Две прямые, перпендикулярные одной и той же плоскости, параллельны.
Теорема 3.Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая к ней перпендикулярна
Перпендикулярность плоскостей
Определение перпендикулярных плоскостей:
Две пересекающиеся плоскости называются перпендикулярными , если третья плоскость, перпендикулярна прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.
Две плоскости называются перпендикулярными, если угол между ними 90°.
Признак перпендикулярности плоскостей
Теорема: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны .
Свойства перпендикулярных плоскостей
Теорема. Плоскость, перпендикулярная прямой пересечения двух плоскостей, перпендикулярна каждой из этих плоскостей
Понятийный аппарат
по теме: «Перпендикуляр и наклонная»
Определения:
Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
Наклонной, проведённой из одной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной.
Проекцией наклонной называется отрезок, соединяющий основания наклонной и перпендикуляра, проведённых из одной и той же точки.
Теорема о свойствах наклонных:
Если из точки вне плоскости проведены к этой плоскости перпендикуляр и наклонные, то: 1) две наклонные, имеющие равные проекции, равны; 2) из двух наклонных та больше, проекция которой больше; 3) перпендикуляр короче любой наклонной.
Теорема о трёх перпендикулярах:
Теорема (прямая): Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной.
Теорема (обратная): Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
Расстояния в пространстве
Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.
Расстоянием от прямой до параллельной ей плоскости называется расстояние от любой точки этой прямой до плоскости.
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них.
Свойства точки, равноудаленной
от сторон или вершин многоугольника
1.Если точка равноудалена от вершин многоугольника, то она проектируется в центр окружности, описанной около многоугольника.
2. Если точка равноудалена от сторон многоугольника, то она проектируется в центр окружности, вписанной в многоугольник.
Углы в пространстве
Определения:
Две пересекающиеся прямые образуют смежные и вертикальные углы. Вертикальные углы равны, а смежные дополняют друг друга до 180°. Угловая мера меньшего из них называется углом между прямыми.
Углом между прямой и плоскостью называется угол между прямой и ее проекцией на данную плоскость
Угол между прямой и ее проекцией на данную плоскость является наименьшим из всех углов, которые образует эта наклонная с прямыми, проведенными в этой плоскости через основание наклонной.
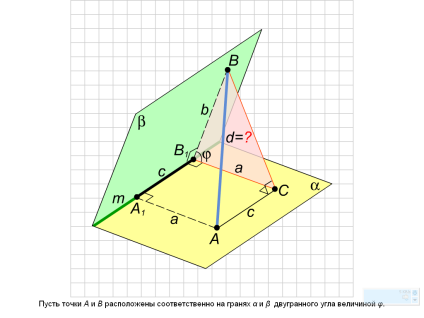
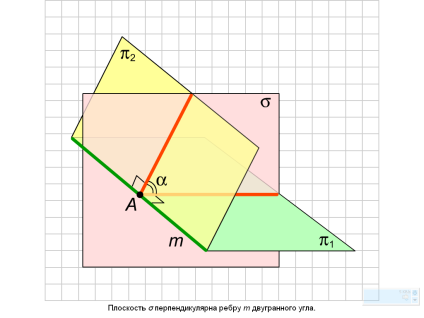
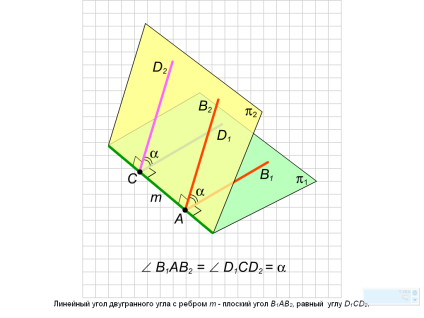
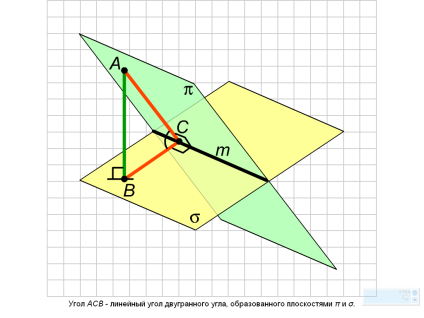
Углом между пересекающимися плоскостями называется угол между прямыми, проведенными в этих плоскостях перпендикулярно прямой их пересечения.
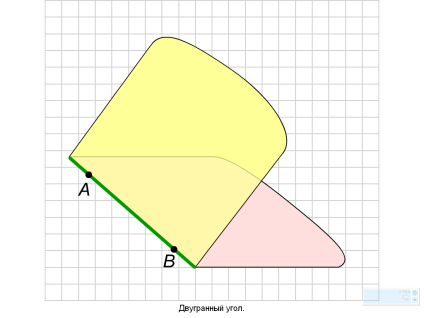
Двугранным углом называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой. Полуплоскости, образующие двугранный угол, называют его гранями , а ограничивающую их прямую- ребром двугранного угла.
Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.