Разработка элективного курса по теме 'Многоликие многочлены' для 9 классов

РАЗРАБОТКА ЭЛЕКТИВНОГО КУРСА ПО ТЕМЕ «МНОГОЛИКИЕ МНОГОЧЛЕНЫ» ДЛЯ УЧАЩИХСЯ 9-Х КЛАССОВ

Математическое образование в системе основного общего образования занимает одно из ведущих мест, что определяется безусловной практической значимостью математики, ее возможностями в развитии и формировании мышления человека, ее вкладом в создание представлений о научных методах познания действительности.

Актуальным остается вопрос дифференциации обучения математике, позволяющей, с одной стороны, обеспечить базовую математическую подготовку, а с другой - удовлетворить потребности каждого, кто проявляет интерес и способности к предмету.

В рамках Концепции профильного обучения на старшей ступени общего образования (приказ МО РФ№2783 от 18.07.2002)для более полного учета интересов, склонностей и способностей учащихся, их намерений в отношении продолжения образования вводиться данный элективный курс «Многоликие многочлены».

Целью изучения предлагаемого курса является создание условий для существенной дифференциации содержания образования, с широкими и глубокими возможностями для осознанного выбора профиля на старшей ступени обучения.

Задачи курса:

• создать положительную мотивацию для дальнейшего обучения на физико-математическом профиле;

• систематизировать знания о многочленах, подготовить необходимый аппарат для решения уравнений;

• познакомить учащихся с ведущими для данного профиля видами деятельности;

• продолжить выработку навыков самостоятельной работы с источниками информации.

Курс целесообразно предлагать учащимся 9 классов в начале учебного года, когда по базовой программе изучается тема «Квадратный трехчлен». Понятия, вводимые на основных уроках, находят свое продолжение на занятиях элективного курса. Вместе с тем совершенствуются навыки тождественных преобразований, в частности, разложение на множители, что необходимо в 9 классе для успешного прохождения итоговой аттестации.

Знакомство с различными видами многочленов: однородными, симметрическими и т.п. - способствует расширению арсенала приемов для решения уравнений соответствующего вида, что, несомненно, помогает школьникам решать задачи повышенной сложности и вырабатывает системный подход в решении уравнений. Эти умения актуальны для успешной сдачи ЕГЭ в 11 классе.

Несмотря на традиционность темы, идеология предпрофильного обучения требует включения в материал элементов нового знания. Современная алгебра опирается на понятие «операция». Знакомство с операциями на доступном уровне вошло в данный курс.

Методы обучения:

• объяснительно- иллюстративный;

• практические методы;

• самостоятельная работа учащихся;

• сочетание индуктивного и дедуктивного методов. Одним из основных методов изложения материала на многих занятиях курса является обобщение, что способствует развитию логической культуры учащихся.

Технологии обучения:

• современная традиционная технология;

• элементы технологии обучения на основе решения задач;

• элементы проектной технологии;

• по возможности, уместно использовать ИТК.

Формы обучения:

• фронтальная;

• групповая;

• контрольно - оценочная;

• взаимоконтроль.

Предполагаемые результаты:

Одним из основных умений, которое должно совершенствоваться, в том числе и на занятиях данного элективного курса, умение работать с учебной и иной литературой. В процессе работы учащиеся должны познакомиться с несколькими книгами для внеклассного чтения по математике.

В результате изучения курса учащиеся должны уметь:

• Выполнять деление многочленов «столбиком» по схеме Горнера;

• Уверенно выполнять разложение на множители сложных выражений;

• Применять изученные свойства многочленов к решению задач.

Формы контроля:

• Презентация прочитанной статьи;

• Сборник занимательных задач по теме (из литературы);

• Создание банка заданий по теме «Делимость многочленов»;

• Итоговая контрольная работа.

Содержание элективного курса

Понятие многочлена с одной переменной и связанные с ним простейшие понятия и их свойства: коэффициенты, стандартный вид, равенство многочлена, старший коэффициент, степень. Нулевой и единичный коэффициент.

Нахождение рациональных корней многочлена с целыми коэффициентами. Стандартные теоремы о целых и дробных корнях. Следствие теоремы, о том, что многочлен с целыми коэффициентами и старшим коэффициентом 1 имеет либо целые, либо рациональные корни. Количество корней многочлена и соответствующего уравнения.

Схема Горнера. Деление многочлена «столбиком». Деление многочлена с остатком. Теорема Безу и ее следствия. Примеры применения следствий при решении уравнений.

Таблица 1

Тематическое планирование:

№

Тема занятия

Количество часов

1.

Многочлены с одной переменной.

1 ч.

2.

Поиск рациональных корней многочлена.

1 ч.

3.

Запуск проекта «Листая книги по математике».

1 ч.

4.

Схема Горнера.

1 ч.

5.

Деление во множестве многочленов.

2 ч.

6.

Теорема Безу.

1 ч.

7.

Контрольная работа.

1ч.

Итого:

8 ч.

Фрагменты уроков

Методическая часть

Поскольку содержание темы традиционное и полно изложено в литературе нет необходимости в данной работе излагать содержание темы. Один из вариантов удачного и современного изложения темы предлагается в учебнике Дорофеева и задачнике к этому учебнику.

Для организации индивидуального контроля по теме неоценимую помощь окажут пособия С.Я и И.Э Гриншпон, в которых представлены дидактические материалы по всем предлагаемым темам.

В методических комментариях представлены следующие материалы:

• Перечень вопросов, рассматриваемых на соответствующих занятиях.

• Примеры реализации деятельностного подхода в обучении.

• Темы рефератов.

• Техническое задание для проекта «Листая книги по математике».

Занятие №1. Что такое многочлен?

1. В этой теме рассматривается понятие многочлена с одной переменной и связанные с ним простейшие понятия и их свойства: коэффициенты, стандартный вид, равенство многочлена, старший коэффициент, степень.

2. Уместно обсудить проблемы, связанные с нулевым и единичным коэффициентом, а также вопрос о том, какие выражения являются многочленами.

3. Логически развитый ученик должен понимать, что судить о вопросе принадлежности выражения к данному классу только по внешнему виду нельзя. (Выражения 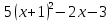, 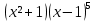являются многочленами, а выражения 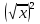, , 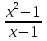не являются).

4. Полезными при решении задач будут следующие свойства:

• Старший коэффициент произведения многочленов равен произведению старших коэффициентов множителей.

• Свободный член произведения многочленов равен произведению свободных членов сомножителей.

• Степень произведения многочленов равна сумме их степеней.

• Свободный член многочлена равен его значению при х=0.

• Значение многочлена при х=1 равно сумме его коэффициентов.

5. Для закрепления свойств можно предложить следующие задачи:

- Найти сумму коэффициентов многочлена .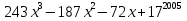

- Найти старший коэффициент многочлена

.

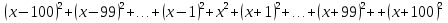1. В качестве домашнего задания предлагается познакомиться с книгой Л.Ф.Пичурина «За страницами учебниками алгебры». В этой работе должны принять все учащиеся.

• 1 группа. «Переходим к третьему киту»;

• 2 группа. «А как было у древних?»;

• 3 группа. «Снова про обобщение».

Поскольку автор книги блестящий публицист и популяризатор математики, знакомство с книгой принесет не только пользу, но и удовольствие.

7. При поиске корней многочлена часто приходиться раскладывать на множители. В ряде случаев полезным оказывается метод неопределенных коэффициентов. Автором этого метода является Рене Декарт.

8. В качестве домашнего задания предлагается познакомиться с жизнью и деятельностью Декарта.

Занятие №2. Рациональные корни многочлена.

1. В качестве проверки домашнего задания предлагается в пяти минутном выступлении каждой группы в тезисной форме изложить содержание прочитанного.

Уместно именно здесь заявить темы рефератов:

• Геометрическая алгебра древних.

• Новый взгляд на алгебру (по книге МПИ « Алгебраические дроби», глава «Ксюша на Кварте, или взгляд на алгебру с космических высот).

• Треугольник Паскаля.

2. В теме решается вопрос о нахождении рациональных корней многочлена с целыми коэффициентами.

3. Приводятся стандартные теоремы о целых и дробных корнях.

4. Следствие теоремы, о том, что многочлен с целыми коэффициентами и старшим коэффициентом 1 имеет либо целые, либо рациональные корни, позволяет решать многие задачи с иррациональными числами.

5. Алгоритм поиска рациональных корней должен быть отработан до уровня навыка и поэтому в этой теме необходимо большое число упражнений.

6. Кроме этого, полезно обсудить терминологический вопрос о количестве корней многочлена и соответствующего уравнения.

Занятие №3. Запуск проекта «Листая книги по математике».

Урок проходит в библиотеке. Ученикам представлен доступ к книгам и журналам. Работа организована по группам.

Цели проектной деятельности:

• Познакомить учащихся с литературой по математике.

• Начать формирование умений работы с учебной и научной литературой.

• Познакомить учащихся с нестандартными задачами и их решениями.

• Готовить учащихся к олимпиадам.

Техническое задание:

1. Просмотреть сборники олимпиадных задач, книги по занимательной математике, подшивки журналов «Квант» на предмет поиска интересных задач о многочленах.

2. Разобрать предложенные решения, попробовать вычленить метод решения, составить указания для решения предлагаемых задач.

3. Подготовить презентацию книг (статей) на итоговой конференции.

4. Подготовить сборник нестандартных задач по теме «Многочлены».

Занятие №4. Схема Горнера.

1. Важным инструментом в решении задач на многочлены является схема Горнера. Не смотря на то, что при применении этой схемы учащиеся могут испытывать определенные затруднения, но, сэкономив время и силу учащихся на изучении данной темы, мы рискуем потерять ее как эффективный метод быстрого нахождения значений многочлена, поиска рациональных корней, деления с остатком и др.

2. Кроме этого, данный материл, работает на развитие алгоритмической культуры, так как эта схема используется в реальных компьютерах. Изучение темы можно провести и путем выстраивания межпредметных связей с информатикой.

3. В качестве возможного варианта изучения темы можно предложить работу с электронным учебником - справочником «Алгебра 7 - 11класс», в котором рассмотрена эта тема и предложены упражнения для отработки.

Занятие №5 -6. Деление многочленов.

1. Эта тема позволит повторить известные свойства делимости чисел и убедиться, что многие из них выполняются и во множестве многочленов, а доказательства отличаются только терминологией и символикой.

2. В теме необходимо отработать алгоритм деления многочленов «столбиком». Это совершенствует вычислительные навыки.

3. Один из уроков можно провести в компьютерном классе с электронным учебником - справочником «Алгебра 7 - 11класс».

4. В качестве домашнего задания придумать 3 примера на деление многочленов. Постараться при этом отразить разные случаи (делание с остатком и нацело, присутствие нулевых коэффициентов и др.). Эти задания нужны для работы в парах на следующем уроке.

5. Индивидуальное задание: книги Л.Ф. Пичурина «За страницами учебника алгебры» пункт «необычное деление».

Переходим к третьему киту.

• Проверь, как ты умеешь преобразовывать многочлены к стандартному виду.

• Для многочленов, так же как для целых чисел всегда выполняются операции сложения, вычитания, умножения. Операция деления выполнима не всегда.

• Можно изучать некоторые общие свойства совершенно различных множеств - различным по свойствам элементам, но «похожих» по поведению относительно некоторых операций.

• Определение кольца.

• Аксиомы алгебры многочленов.

• Для возможности делить многочлены вводят рациональные выражения.

• Проверь себя на нескольких упражнениях на действия с рациональными выражениями.

А как было у древних?

• Читайте классиков.

• Геометрическая алгебра Евклида.

• Геометрический распределительный закон.

• Геометрическое доказательство формулы квадрата суммы.

• Геометрический вывод формулы

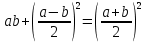
• Изопериметрические задачи.

Снова про обобщения.

• Квадрат суммы нескольких слагаемых.

• Бином Ньютона.

• Треугольник Паскаля.

Занятие №7. Теорема Безу.

Теорема Безу относится к основным факта теории многочленов. Она позволяет доказать рад следствий, которые находят широкое практическое применение при решении уравнений высших степеней.

Также можно предложить творческие задания, например, объединить детей в группы и на темы: «История многочленов», «Вклад Горнера в тему многочлены», «Безу - знаменитый математик», «Треугольник Паскаля», «Бином Ньютона», сделать стен газеты, написать рассказы, доклады, приготовить презентацию.

Занятие №8. Контрольная работа.

Занятие можно провести в компьютерном классе с электронным учебником - справочником «Алгебра 7-11 класс» в режиме зачета.

А можно предложить контрольную работу.

Таблица 2

Вариант № 1

Вариант №2

1)Разложите на множители многочлен: х⁴+3х³-5х²-6х-8

1)Разложите на множители многочлен: х⁴-х³-7х²+13х-6

2)Найти корни многочлена по схеме Горнера:

а) f (x) = x ³ + 2 x ² - 5 x - 6;

2)Найти корни многочлена по схеме Горнера: f (x) = x ⁵ - 5 x ⁴ + 6 x ³ - x ² + 5 x - 6

3) Выполнить деление «углом».

P(x) = x⁴ + x³ + 2x² + x +1

на Q(x) = x² - x + 1

3)Выполнить деление «углом».

P(x) = х⁴ + 2х³-3х² + 5х-2

на Q(x) = х²-2х-2

4)Найти значение многочлена Р₅(х) = 2х⁵ - 4х⁴ - х² + 1 при х = 7.

4)Найти значение многочлена Р₆(х) =х⁶-4х⁴ + х³-2х² + 5 при х = 3.

5)При каком значении а многочлен 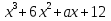делиться на ?

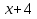5)При каком значении а многочлен 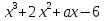делиться на ?

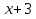Задания, используемые учеником для проверки знаний и учителем для методических работ по предложенной теме

Из анализа литературы и бесед с учителями математики, был выявлен следующий факт, что существует множество литературы, сборников, содержащих задания по теме «Многочлены», но, во-первых, учитель не всегда имеет возможность предложить их детям на уроках в связи с тем, что время на прохождение темы ограничено, во - вторых, формулировка и содержание заданий носят скучный характер, что часто вызывает негатив у учащихся, снижение интереса к их выполнению.

В связи с этим возникла необходимость подобрать и разработать задания, позволяющие развить творчество, повысить интерес к предмету математики, углубить знания по изучаемой теме.

Таким образом, в каждой теме предложенного элективного курса задания классифицируются следующим образом:

- задания с элементами занимательности, делают занятие более увлекательным, способствуют активизации знаний ребят, расширению кругозора, поддержание интереса к предмету, формированию гибкости ума, освобождению мышления от шаблонов;

- задания творческого характера, способствуют развитию творческих способностей, максимально вовлечь учащихся в процесс обучения, формированию познавательного интереса к математике, развитию интеллектуальных умений учащихся, повышается качество знаний, уровень исследовательской деятельности;

- задания повышенного уровня сложности, направлены на то, что степень самостоятельности школьников со временем возрастала, а помощь учителя постепенно снижалась. Сильные учащиеся нуждаются в заданиях повышенной трудности, нестандартных работах творческого характера, именно это позволит им максимально реализовать и развить свои учебные возможности.

Рассмотрим задания с элементами занимательности:

Задание 1.Заполните пропуски:

2х * 3х³= ...

а³с * 2а²в= ...

2а* ... =-18к³а³р

-15х³у²/ ... =5ху

(20х²- ... ):4х=5х-1

... *(5х-4)= 10х-8

…/…=2а³в

(-4у²-6х²)/…=2у²+3х²

2*(-2у+ ... )=-4у-6х

-18к³р³п:9кр²= ...

( ... -3х)*(5-4у)=10-15х- ... + ...

( ...-... )* ... =ав+5а-2в-10

( ...-... ) * +(...-…)=ск-2с+к²-2к

Это задание направленно на отработку действий над многочленами, на формирование и развитие таких способностей как внимание, мышление, логических приемов мыслительной деятельности, познавательной активности и самостоятельности.

Задание 2. Игра «Поле чудес»:

У каждого карточка с заданием, на доске таблица ответов. Номер вашей карточки соответствует порядковому номеру буквы, которая находится в таблице ответов, по выполнению задания, таблица заполняется буквами. Составить зашифрованное высказывание и объяснить правила расстановки знаков препинания.

Таблица 3

1

2

3

4

5

6

7

5

8

9

1

10

5

11

5

12

13

1

14

15

5

11

6

1

14

1

9

10

16

17

1

18

Задания на карточках:

Таблица 4

Выполняя задания, ученик раскладывает на множители с помощью формул сокращенного умножения, способа группировки и приведением подобных слагаемых.

Скажите, все ли знаки препинания здесь стоят? Это задание направленно на интеграцию предметов математики и русского языка.

Задание 3. Тест по теме: "Разложение многочлена на множители с помощью формул сокращенного умножения".

Выберите себе вариант, внимательно прочитайте задание. К каждому заданию даны три ответа, из которых один верный. Решите задание, сравните полученный ответ с предложенным.

Таблица 5

I вариант

Таблица 6

II вариант

Таблица 7

III вариант

В бланке ответов под номером задания поставьте букву в клеточке, которая соответствует выбранному ответу. Перед самопроверкой учащиеся сдают бланки учителю, затем сверяют свои ответы и ставят себе оценки.

Задание 4.

Таблица 8

1) Найдите ошибку:

1. 3х (х-3)=3х²-6х;

2. 2х+3ху=х(2+у);

3. (8+3х)(2х-у)=16х-8у+6х+3ху;

4. х(а+с)-2 (а+с)=(а+с)(х+2).

2) Вставьте пропущенное выражение:

1. 5х(2х²-х)=10х³-…;

2. -3ау-12у=-3у (а+…);

3. (а-5)(11-в)=11а-ав-55+…;

4. (в-с)-а(с-в)=(в-с)(…).

Задание 5. Игра с действиями.

Я многочлен от слова «много»
Во мне всегда звучит тревога:
Как одночлены все собрать,
В какую сумму записать?
Живу всегда с друзьями в мире,
Люблю играть в примеры с ними,
А знаки «плюс», «отнять», «умножить»
Всегда играть готовы тоже.
Так вот, мой друг, сейчас давай-ка
В игру вот эту поиграй-ка.
Даю тебе два выраженья
Ты результат найди сложенья,
Затем я знаки поменяю
И все примеры прорешаем.

Даны два выражения, которые нужно сложить, вычесть из первого выражения второе, умножить.

а) (8+3х) и (2у-1);

б) (m²-2n) и (m²+3n).

Задание 6. Игра «Математическое лото».

Учащимся предлагается большая карта с заданиями и маленькие карточки с ответами. Выполнив задание на большой карте, необходимо найти результат на маленькой карточке и этой карточкой накрыть соответствующее задание на большой карте. Чтобы проверить результат, нужно перевернуть маленькие карточки, обратная сторона которых содержит какой-либо рисунок, если рисунок получился, то учащийся выполнил задание верно.

Таблица 9

Вариант I

Карточки с ответами

Таблица 10

Вариант II

Карточки с ответами

Задание 7. Тест

1. Выполните умножение многочленов (а² - 2b³)(7a²b² + 6a - 3b²) и укажите степень получившегося многочлена.

а) 8; б) 7; в) 6; г) 5.

2. Приведите многочлен (3х - 7у)(2х + 3у) - (4х - 5у)(3х + у) к стандартному

виду.

а) -6х²-16ху-26у²; б) -6х²+6ху-16у²; в) 18х²-16ху-26у²; г) -6х²+6ху+16у².

3. Укажите количество корней уравнения 3х³ = -27х.

а) нет корней; б) 1 корень; в) 2 корня; г) 3 корня.

4. Разложите на множители 4m² - n + 2m - n².

а) (2m-n)(2m+n+1); б) (2m+n)(2m-n+1); в) (2m-n)(-n+2m); г) (2m+1)(2m-n²-n)

5. Выполните деление многочленов (6с³-19с²+31с-14) : (3с-2).

а) 2с² - 7с + 15; б) 2с + 7; в) 2с² - 5с - 7; г) 2с² - 5с + 7.

Задание 8.

Дети знакомы с тождеством 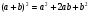, им предлагается игра «Лабиринт», показанная на рисунке 2, как одно из средств самоконтроля.

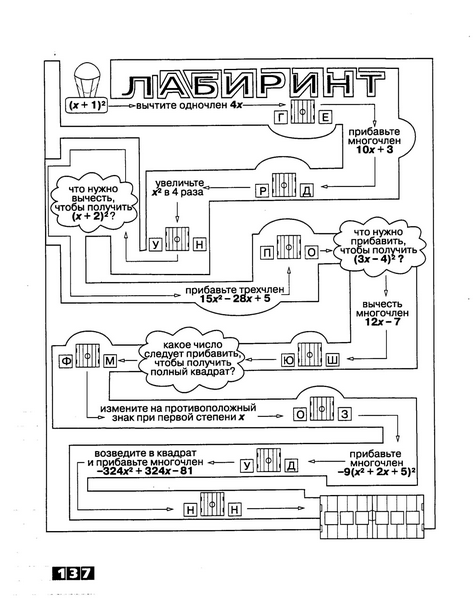
Рис. 1. Игра «Лабиринт»

При этом учащимся дается следующая инструкция: путешествуя по лабиринту, помните: чтобы открыть последнюю дверь, вам необходимо собрать шесть обусловленных драгоценных камней. Вы отыщете их, если правильно выполните задания. У каждого входа нужный камень находится справа от двери (по ходу движения), если к этому моменту получается полный квадрат разности, и слева, если - квадрат суммы.

Далее представлены задания творческого характера:

Задание 1. Составьте кроссворд.

Задание творческого характера - составление кроссворда, где ученик обобщает теоретический материал по изученной теме. Например, задание сделанное учеником может выглядеть так. Задание: составьте кроссворд по теме «Действия над многочленами», также проектируется взаиморешение кроссвордов.

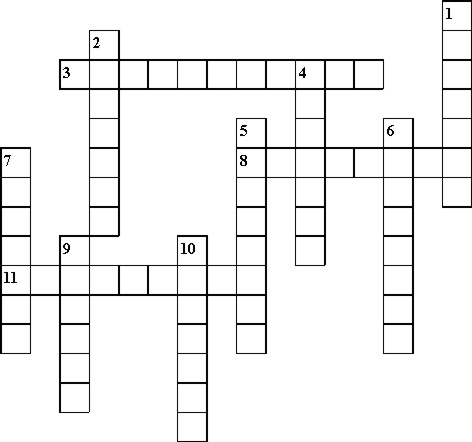
По вертикали:

1. Произведение, состоящее из одинаковых множителей (степень).

2. Какова степень одночлена 7а³b⁴с (восьмая).

4. Показатель степени, который обычно не пишут (единица)

5. Слагаемые, отличающиеся только коэффициентами (подобные).

6. "А ну-ка, отними!" наоборот (сложение).

7. Какова степень многочлена 2а⁶ + а - 1 - 3а⁴ + а⁷?

9. Число, при подстановке которого в уравнение, получается верное равенство (корень).

10. Раздел математики (алгебра).

По горизонтали:

3. Числовой множитель, стоящий перед буквенным выражением (коэффициент).

8. Произведение чисел, переменных и степеней переменных (одночлен).

11. Сумма одночленов (многочлен).

Задача повышенного уровня сложности может звучать следующим образом: При каком целом значении 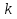один из корней уравнения втрое меньше другого?

Подобные задания увеличивают математическую культуру и развитие математической речи, так же логического мышления, привитие интереса к предмету, воспитание прилежания, самостоятельности, точности, аккуратности.

Задание 2. Сочините задачу по теме «Многочлены».

Детям предлагается составить задачу, связанную непосредственно с темой многочлены. Например, она может звучать так:

Колхоз планировал провести сев за 14 дней. Перевыполнил план, колхозники засевали в день на 30 га больше, чем планировалось, и уже за 4 дня до срока им оставалось засеять только 20 га. Сколько гектаров должен был засеять колхоз?

Обозначим дневную норму сева в (га) буквой х, тогда

1) Сколько всего га должно был засеять колхоз 14х.

2) Сколько га засевалось за 1 день х + 30.

3) Сколько га было засеяно за 4 дня до срока 10 * (х + 30).

Сравните число засеянных за 4 дня до срока, с числом га, которые планировал засеять колхоз за 14 дней, и напишите уравнение.

14х = 10 * (х +30) + 20

х = 80 га

120 га должен был засеять колхоз.

Задание 3.Математические сочинения.

Одной из форм творческой работы учащихся при обучении математике являются математические сочинения. Сочинение развивает самостоятельность мышления школьников и умение кратко изложить текст в письменной форме. При написании математических сочинений ученики выполняют разные виды деятельности:

1) самостоятельные изучения литературы;

2) отбор материала по выбранной теме;

3) связное изложение материала;

4) проведение небольших самостоятельных исследований;

5) подбор или самостоятельное составление задач и их решение.

Тематика сочинений разнообразна. Например: «История многочленов» .

Приложение математики в какой-нибудь области знаний «Применение многочленов в области техники».

Задание 4. Написать доклад на темы: «История многочленов», «Вклад Горнера в тему многочлены», «Безу - знаменитый математик», «Треугольник Паскаля», «Бином Ньютона».

Задание 5. Составьте контрольную работу по теме:

«Действия над многочленами»;

«Нахождение корней многочлена»;

«Схема Горнера и теорема Безу»;

«Производная многочлена».

Оцените сложность выполнения каждого задания (в баллах), и уровень сложности всей контрольной работы.

Закончим классификацию заданиями повышенного уровня сложности:

Задание 1.

а) Найти НОД ((x ⁶ - 1);(x ⁸ - 1)) по алгоритму Евклида.

Решение: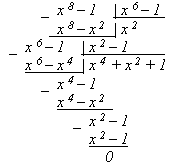

НОД ((x ⁶ - 1);(x ⁸ - 1)) = x ² - 1.

Задание 2. Узнайте, делится ли многочлен f(x) = x ⁵ - 5 x ⁴ + 8 x ³ - 5 x ² + x + 2 на (x - 1), (x + 1), (x - 2)

Решение: По теореме Безу, если f(1) = 0, то f(x) делится на (x - 1). Проверим это.

f(1) = 1 - 5 + 8 - 5 + 1 + 2 > 0, f(x) не делится на (x - 1);
f(-1) = - 1 - 5 - 8 - 5 - 1 + 2 < 0, f(x) не делится на (x + 1);
f(2) = 32 - 80 + 64 - 20 + 4 = 0, f(x) делится на (x - 2).

Задание 3. Многочлен P(x) при делении на (x - 1) дает остаток 3, а при делении на (x - 2) дает остаток 5. Найти остаток от деления многочлена P(x) на (x ² - 3 x + 2).

Решение:

P(x) = (x - 1) Q ₁(x) + 3 (1)
P(x) = (x - 2) Q ₂(x) + 5 (2)
Из (1) и (2) следует, что P(1) = 3, P(2) = 5.
Пусть P(x) = (x ² - 3 x + 2) Q (x) + a x + b или
P(x) = (x - 1) (x - 2) Q (x) + a x + b (3)

Подставив в (3) последовательно x = 1 и x = 2, получим систему уравнений, из которой a = 2, b = 1.

Ответ: 2 x + 1.

Задание 4. При каких m и n многочлен x ³ + m x + n при любых x делится на x ² + 3 x + 10 без остатка.

Решение: При делении "уголком" получим x ³ + m x + n = (x ² + 3 x + 10) (x - 3) + ((m - 1) x + (n + 30)).

Т.к. деление выполняется без остатка, то (m - 1) x + (n + 30) = 0, а это возможно (при любом x) только в случае, когда m = 1, n = -30.

Ответ: m = 1, n = -30.

Задание 5. Применяя схему Горнера, узнайте, делится многочлен (x) = x ⁵ - 5 x ⁴ + 8 x ³ - 5 x ² + x + 2 на (x - 1), (x + 1), (x - 2). Если требуется проверить несколько значений, то для экономии выкладок строят одну объединенную схему.

В последнем столбце в третьей, четвертой и пятой строках - остатки от деления. Тогда f(x) делится без остатка на (x - 2), т.к. r = 0.

Задание 6. Найти корни многочлена f(x) = (x ⁴ - x ³ - 6 x ² - x + 3).

Решение: Делители свободного члена: - 1, 1, - 3, 3 могут быть корнями многочлена. При x = 1 очевидно сумма коэффициентов равна нулю. Значит, x₁ = 1 - корень. Проверим по схеме Горнера на корень число - 1 и другие делители свободного члена.

1

- 1

- 6

- 1

3

- 1

1

- 2

- 4

3

0

- 1

1

- 3

- 1

4

3

1

1

- 1

0

x = -1 - корень
второй раз x = -1 - не корень
проверим x = 3
x = 3 - корень.
f(x) = (x + 1) (x - 3) (x ² + x - 1), x ² + x - 1 = 0,

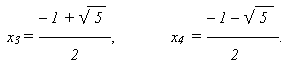
Задание 7. Табличный процессор Excel можно применить для графического решения уравнений третьей степени. Из курса математики нам известно, что корнями уравнения являются значения точек пересечения графика функции с осью абсцисс. С помощью программы Excel можно строить практически любые графики. Но графическое решение дает только приблизительные результаты.

Решите уравнение: х³-2х²+4х-12=0

Это уравнение мы решим с помощью программы EXCEL.

Алгоритм будет следующий:

1. Построим таблицу: в ячейку А2 заносится начальное значение аргумента х=0, для автоматического заполнения всего столбца нужно в ячейку А3 занести формулу А2+0,15 и скопировать её до ячейки А20.

2. При заполнении столбца В в ячейку В2 заносится формула А2*А2*А2-2*А2*А2+4*х-12, которая затем копируется до ячейки В20.

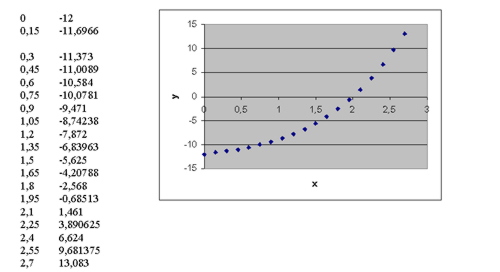
С помощью мастера диаграмм выберем тип диаграммы точечная и построим диаграмму.

На диаграмме видно, что график данной функции имеет точку пересечения с осью ОХ, которое является решением. х=1,9

Ответ: х=1,9

Таким образом, мы видим, что используя программу Excel можно графически решить практически любое уравнение.

Подобные задания повышают интерес, что повышает математическую культуру и интерес подготовленности по математике.

Задание 8.

Определите a и b так, чтобы -2 было корнем многочлена

P(x) = x⁵ + ax² + bx + 1, имеющим, по крайней мере, кратность два.

Решение: Если -2 - корень многочлена P(x) кратности два, P(x) делится на

(x + 2)² без остатка (R = 0)

(x + 2)² = x² + 4x + 4

_x⁵ + ax² + bx + 1 x² + 4x + 4

x⁵ + 4x⁴ + 4x³ x³ - 4x² + 12x - (a + 32)

_-4x⁴-4x³-ax²+bx+1

-4x⁴ - 16x³ - 16x²

_12x³ + (16 - a)x² + bx + 1

12x³ +48x² + 48x

_-(a + 32)x² + (b - 48)x + 1

-(a + 32)x² - 4(a + 32)x - 4(a + 32)

(4a +b - 48 + 128)x + 4a + 129

R = (4a +b - 48 + 128)x + 4a + 129 = (4a +b + 80)x + 4a + 129

Но R = 0 , значит

(4a +b + 80)x + 4a + 129 = 0 при любых x .

Это возможно при условии, что

4a +b + 80 = 0 ,

4a + 129 = 0. Решим систему двух уравнений:

4a +b + 80 = 0 a = -32,25

4a + 129 = 0 b = 49

Ответ: a = -32,25 , b = 49 .

Подобные задания увеличивают математическую культуру и развитие математической речи, так же логического мышления, привитие интереса к предмету, воспитание самостоятельности, точности и аккуратности.