Конспект урока по геометрии в 8 классе. Решение задач по теме «Площадь треугольника»

Конспект урока

Решение задач по теме: «Площадь треугольника».

8 класс

Учитель: Юшко Любовь Леонидовна

МБОУ СОШ №2 г.Волгореченск, Костромской обл.

Цель урока: доказать теорему о площади треугольника, рассмотреть следствия из этой теоремы и первичное применение теоремы к решению задач.

Задачи урока:

1) научиться применять теорему о площади треугольника для решения задач;

2. развивать внимание, память, логическое мышление; активизировать мыслительную деятельность, умение анализировать, обобщать и рассуждать;

3. воспитание трудолюбия, усердия в достижении цели, интерес к предмету.

Оборудование урока: доска, разноцветный мел, разноцветные маркеры.

Тип урока: изучение нового материала.

Орг.форма: традиционная.

План урока:

1. Организационный момент, домашнее задание (3 мин.)

2. Устная работа, проверка домашнего задания (15 мин.)

3. Подготовительный этап (3 мин.)

4. Изучение теоретического материала (7 мин.)

5. Закрепление, решение задач (10 мин.)

6. Итог урока (2 мин.)

Доска в начале урока:

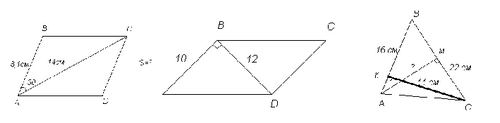
Ход урока:

1. Организационный момент:

В начале урока два ученика готовят домашнее задание на доске. Учитель обобщает знания ребят, полученные на прошлом уроке. Сообщает ученикам план сегодняшнего урока. Просит записать домашнее задание в дневник.

Учитель:

На прошлом уроке мы доказали теорему о вычислении площади параллелограмма

Сегодня на уроке мы проверим домашнее задание, решим одну устную задачу и в результате решения задачи определим тему и цель урока.

Домашнее задание: п.52, вопрос 5, №466, 468(а,г), 470.

2. Устная работа:

Учитель:

Что называют площадью многоугольника?

Каким числом выражается площадь многоугольника?

Что показывает это число?

Как вы понимаете смысл слов: «Площадь комнаты равна 18 м²»?

Сформулируйте основные свойства площадей многоугольников.

Чему равна площадь квадрата?

Сформулируйте теорему о вычислении площади прямоугольника.

Ученик:

• Площадь многоугольника - это величина той части плоскости, которую занимает многоугольник.

• Площадь многоугольника выражается положительным числом.

• Это число показывает сколько раз единица измерения и ее части укладываются в данном многоугольнике.

• Это значит, что в комнате помещается 18 квадратов со стороной 1 метр.

• Равные многоугольники имеют равные площади. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

• Площадь квадрата равна квадрату его стороны.

• Площадь прямоугольника равна произведению его смежных сторон.

Сформулируйте и докажите теорему о вычислении площади параллелограмма.

(1 ученик доказывает эту теорему на доске)

Площадь параллелограмма равна произведению его основания на высоту. (§ 2, п.51)

№ 462 (решает 2 ученик)

Сторона ромба равна 6 см, а один из углов равен 150⁰. Найдите площадь ромба.

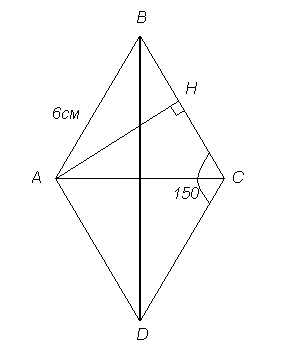
Рассмотрим треугольник АВН. Он прямоугольный, угол В равен 30⁰. Катет в прямоугольном треугольнике, лежащий напротив угла в 30⁰, равен половине гипотенузы. Следовательно, АН = 3 см. S_ABCD=ВС*АН=6*3=18 (см²).

Учитель:

Найдите площадь параллелограмма, изображенного на рисунке.

(решение ученики комментируют с места)

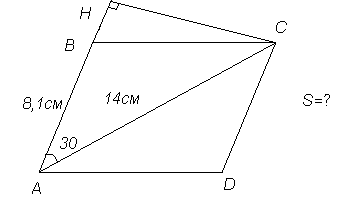
Проведем высоту СН к прямой АВ. Рассмотрим прямоугольный треугольник АНС. Угол А равен 30⁰, следовательно, катет СН равен 7 см. S_ABCD=АВ*СН=8,1*7=56,7 (см²).

3. Подготовительный этап:

Учитель:

Решите задачу.

Дано: АВСD - параллелограмм, ВD - диагональ, АВВD, АВ = 10см, ВD = 12см. Найти:

• площадь параллелограмма АВСD;

• п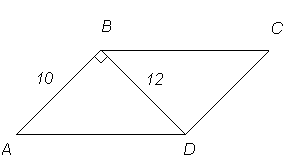лощадь треугольника АВD.

Итак, тема сегодняшнего урока: «Площадь треугольника».

Одну из сторон треугольника часто называют его основанием. Если основание выбрано, то под словом «высота» подразумевают высоту треугольника, проведенную к основанию.

Рассмотрим треугольник АВD. Выберем основание АВ. Назовите высоту треугольника АВD.

Ученик: ВD.

Учитель:

Чему равна площадь треугольника?

Ученик:

Площадь треугольника равна половине произведения его основания на высоту.

4. Изучение теоретического материала :

Дано:

∆АВС;

S - площадь треугольника.

Доказать:

S =АВ*СН.

Доказательство:

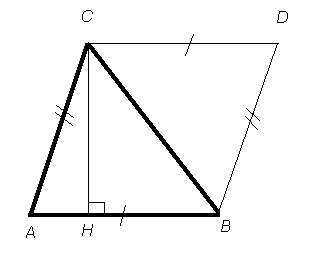
1. Достроим треугольник АВС до параллелограмма АCDВ.

2. ∆АСВ=∆DВС (по трем сторонам) площади треугольников тоже равны площадь S треугольника АВС равна половине площади параллелограмма, т.е.

S =АВ*СН.

■

Учитель:

Начертите прямоугольный треугольник АВС с прямым углом С.

Чему равна площадь прямоугольного треугольника?

Ученик:

S=АС*ВС.

Следствие1. Площадь прямоугольного треугольника равна половине произведения катетов.

Учитель:

• Начертите два различных треугольника АВС и А₁В₁С₁ с равными высотами ВН и В₁Н₁.

• Измерьте основания ваших треугольников.

• Вычислите площади треугольников S и S₁.

• Найдите отношения площадей ваших треугольников.

• Сравните с отношением оснований и сделайте вывод.

Ученик:

Следствие2. Если высоты двух треугольников равны, то их площади относятся как основания.

4. Закрепление, решение задач:

№ 469, 465 (резерв)

№469

С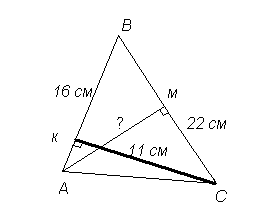тороны АВ и ВС треугольника АВС равны соответственно 16 см и 22 см, а высота, проведенная к стороне АВ, равна 11 см. Найдите высоту, проведенную к стороне ВС.

S_АВС =

S_АВС =

Следовательно, =88; АМ=8 (см).

4. Итог урока:

Учитель:

Чему равна площадь треугольника, площадь прямоугольного треугольника?