- Учителю
- Разработка урока по математике для 8 класса по теме «Решение задач с помощью рациональных уравнений»
Разработка урока по математике для 8 класса по теме «Решение задач с помощью рациональных уравнений»





 муниципальное бюджетное общеобразовательное учреждение
муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 107»
Методическая разработка
Технологическая карта и самоанализ урока по математике в 8 классе
по теме «Решение задач с помощью рациональных уравнений»
Разработала:
Володина Светлана Юрьевна
учитель математики высшей
квалификационной категории
Новокузнецк 2014
Раздел Квадратные уравнения
Тема урока Решение задач с помощью рациональных уравнений
Количество часов на изучение темы - 5, урок 3
Тип урока (типология уроков в дидактической системе деятельностного метода) - урок рефлексии и отработки знаний
Цели урока
Деятельностная: формирование способностей к фиксированию собственных затруднений, выявлению их причин и коррекции собственных действий.
Содержательная: совершенствование умений решения задач с помощью рациональных уравнений.
Развивающая: создание условий для приобретения первоначального опыта математического моделирования, развития интереса к математическому творчеству, развития мышления (умения анализировать, сравнивать, строить аналогии), формирования общеучебных умений.
Воспитательная: воспитание познавательного интереса к математике, ответственности и осмысленной учебной деятельности, коммуникативного умения сотрудничать с одноклассниками и учителем.
Методическая: самоанализ урока при реализации системно-деятельностного подхода на уроках математики в условиях внедрения ФГОС.
Планируемые результаты, в том числе УУД
Предметные: уметь решать задачи с помощью дробно-рациональных уравнений, реализовывая все этапы математического моделирования.
Метапредметные: уметь использовать таблицы для интерпретации информации, понимать сущность алгоритма и уметь действовать в соответствии с алгоритмом, уметь самостоятельно ставить учебные цели, рассуждать по аналогии, делать аргументированные выводы.
Познавательные УУД: уметь выделять необходимую информацию из текстов задач, владеть общим приемом решения задач, переводить словесные формулировки на математический язык, описывать реальные ситуации с помощью математических моделей (уравнений), планировать ход решения задачи, применять алгоритмы решения уравнений, выполнять алгебраические преобразования при решении уравнений, обнаруживать и устранять ошибки арифметического, алгебраического и логического характера.
Личностные УУД: проявлять внимание, познавательный интерес; оценивать собственную учебную деятельность; устанавливать связь между целью деятельности и ее результатом, формировать адекватную самооценку.
Коммуникативные УУД: воспринимать текст с учетом поставленной учебной задачи, находить в тексте необходимую информацию; слушать и понимать речь других; планировать учебное сотрудничество с учителем и сверстниками; осуществлять самоконтроль; организовывать учебное взаимодействие в группе.
Регулятивные УУД: отвечать на вопросы; определять и формулировать цель деятельности на уроке; удерживать цель деятельности до получения ее результата; планировать свои действия; оценивать уровень владения учебным действием (отвечать на вопрос «что я не знаю и не умею?»); осознавать качество и уровень усвоения материала.
Основные понятия темы
Рациональные, квадратные, дробно-рациональные уравнения; математическая модель задачи.
Методы и формы организации деятельности: фронтальная работа, выполнение тестовых заданий, работа в малых группах и парах, самостоятельная работа
Ресурсы: задачник «Алгебра 8» А.Г. Мордковича, мультимедийный проектор и презентация, конверты с задачами и карточками-подсказками, карточки с нестандартными задачами, листы фиксирования результатов деятельности.
Эпиграф урока
Если хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их. Дж. Пойа
Технологическая карта урока
Этапы урока
Задачи этапа
Деятельность учителя
Деятельность учащихся
1.Этап мотивации (самоопределения) к коррекционной деятельности
Создать условия для возникновения внутренней потребности включения в деятельность
Выделить содержательную область деятельности
Сформулировать тему урока
Приветствует обучающихся, проверяет готовность к уроку, организует внимание.
Инициирует мотивационную беседу.
Включаются в деловой ритм урока.
2. Этап фиксации затруднений в деятельности
Подготовить мышление учащихся для выявления места и причины затруднений, осознания ими потребности к исправлению собственных ошибок
Организует самостоятельную работу (тест) для проверки умения составлять уравнение по условию задачи (варианты 1,2 теста на листе фиксирования результатов деятельности - ПРИЛОЖЕНИЕ)
Организует самопроверку работы по готовому образцу с фиксацией своих результатов, (без исправления своих ошибок) (слайды 2-4)
Слайд 5
Зачитывает эпиграф урока. (слайд 6)
Выполняют тест.
Выполняют самопроверку.
Ответы и результат фиксируют в листе результатов
Формулируют тему урока.
3. Этап построения проекта выхода из затруднений
Уточнить индивидуальную цель урока и определить проект выхода из затруднений
Помогает сформулировать индивидуальную цель и составить план деятельности (слайды 7, 11)
Анализируют результаты теста
Выявляют место, в котором допущена ошибка
Уточняют индивидуальную цель дальнейшей деятельности на уроке
4. Актуализация знаний
Актуализировать опорные знания и умения по основным способам решения квадратных, дробно-рациональных уравнений и задач, сводящихся к ним
Организует повторение, способствуя активизации памяти и внимания.
1) Назовите этапы решения задач. (слайд 12)
2) Что является математической моделью задачи?
3) Какие уравнения называются рациональными?
4)Какие выражения являются рациональными?
5) Какие типы рациональных уравнений вы знаете?
6) Что подразумевается под словами «работа с математической моделью»?
7) Решите уравнения (слайд 13)
8) Сформулируйте алгоритм решения квадратного уравнения.
9) Сформулируйте алгоритм решения дробно-рационального уравнения.
Вспоминают и формулируют алгоритмы решения задач и уравнений, применяют теоретические знания, отвечают на вопросы учителя, слушают (исправляют, дополняют) ответы одноклассников.
5. Усвоение способов действий
Решение задач
Способствовать формированию умений и навыков
Выдает задания и необходимые пояснения учащимся, работающим в группах и парах
Задания для работы в группе (карточки -ПРИЛОЖЕНИЕ 2)
Задания для работы в парах (карточки -ПРИЛОЖЕНИЕ 3)
Задания для коллективной работы - (слайды 17,18), для самостоятельной работы: составить уравнение в задачах №№ 27.7, 27.11; решить задачу № 27.18
Все учащиеся могут получить консультацию учителя после окончания коллективной работы.
Учащиеся, работающие в парах, получают вместе с текстом задачи набор подсказок, которыми могут воспользоваться при необходимости; после окончания решения самостоятельно принимают решение о переходе на следующий уровень.
Дополнительное задание для 2 группы: № 27.41
Дополнительное задание для 3 группы: № 27.45
Работают в соответствии с планом:
1. В группе, решая нестандартные задачи
2. В парах, решая задачи на работу, выполняя самопроверку по эталону
3. Коллективно, отвечая на вопросы учителя
4. Самостоятельно, выполняя самопроверку по эталону
6. Рефлексия деятельности
Фиксировать степень соответствия поставленной цели и результатов деятельности
Наметить цели на следующую деятельность, определить задания для работы дома
Дать качественную оценку работы класса и отдельных учащихся.
Инициировать рефлексию учебной деятельности: степени соответствия поставленной цели и результатов:
1. Чему вы научились сегодня на уроке?
2. Сравните свой результат с вашей личной целью (достигли цели или не достигли цели)
3. Запишите этот вывод в оценочный лист.
4. Если вы не достигли цели, что вам помешало (недостаток времени, плохое самочувствие, другое) и что вы можете предпринять для исправления ситуации)
Мотивирует выполнение домашнего задания.
§ 27, № 27.10, №27.17, № 27.27, №27.29, № 27.34 - решить две задачи на свой выбор
Кто повысил свой начальный балл?
Характеризует работу класса.
Объясняет критерии оценок за урок.
Анализируют затруднения в собственной учебной деятельности
Выполняют самооценку результатов деятельности в баллах по предложенной шкале
Записывают домашнее задание в дневник
Литература
-
Алгебра. 8 класс. В 2 ч. Ч.1 Учебник для учащихся общеобразовательных учреждений/[А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. - 13-е изд., сиер. - М.: Мнемозина, 2011.
-
Алгебра. 8 класс. В 2 ч. Ч.1 Задачник для учащихся общеобразовательных учреждений/[А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. - 13-е изд., сиер. - М.: Мнемозина, 2011.
-
Асмолов А. Г. Системно-деятельностный подход в разработке стандартов нового поколения/ Педагогика М.: 2009 - №4. - С18-22.
-
Петерсон Л.Г., Кубышева М.А., Кудряшова Т.Г. Требование к составлению плана урока по дидактической системе деятельностного метода. - М., 2006.
-
Сухов В.П. Системно-деятельностный подход в развивающем обучении школьников. СПб.: РГПУ им. А.И.Герцена, 2004.
-
Шевкин, А.В. Текстовые задачи по математике для учащихся 7-11 классов образовательных учреждений /[А.В. Шевкин] - М.: ИЛЕКСА, 2011.
-
Шубина Т.И. Деятельностный метод в школе http://festival.1september.ru/articles/527236/
ПРИЛОЖЕНИЕ 1 Лист самооценки и фиксирования результатов деятельности
Фамилия, имя____________________________ класс______
1. Тема урока__________________________________________
2. Тест 1 вариант
Прочитайте задачу, заполните таблицу и запишите уравнение по её условию:
1. Велосипедист проехал 18 км с определенной скоростью, а оставшиеся 6 км со скоростью на 6 км/ч меньшей первоначальной. Найдите скорость велосипедиста на втором участке пути, если на весь путь он затратил 1,5 часа.
v, км/ч
t, ч
S, км
Уравнение:
2. Секретарь хочет набрать на компьютере рукопись объемом 450 страниц. Если он будет набирать на 5 страниц в день больше, чем запланировал, то закончит работу на 3 дня раньше. Сколько страниц в день планирует набирать секретарь?
Уравнение:
3. Велосипедист проехал 30 км от города до турбазы. На обратном пути он ехал 2 часа с той же скоростью. а затем на 3 км/ч быстрее и затратил на обратный путь на 6 мин меньше. чем на путь из города до турбазы. какое время затратил велосипедист на обратный путь?
Уравнение:
Количество баллов______________________________________
3. Цель урока__________________________________________________________________________________________________
4. Решение задач (укажите номер задачи или номер карточки)
1) таблица
Уравнение
Ответ:
5. Оценка достижения цели_______________________ в баллах________________________
Тест 2 вариант
Прочитайте задачу, заполните таблицу и запишите уравнение по её условию:
1. Первый пешеход прошел 6 км, а второй пешеход 5 км. Скорость первого пешехода на 1 км/ч меньше, чем скорость второго. Найдите скорость первого пешехода, если известно, что он был в пути на 30 минут больше второго.
v, км/ч
t, ч
S, км
Уравнение:
2. Две машинистки, работая совместно, могут перепечатать рукопись за 8 часов. Сколько времени потребовалось бы каждой машинистке на выполнение этой работы, если одной для этого требуется на 12 ч больше, чем другой?
Урвнение:
3. Велосипедист рассчитывал проехать по маршруту ВС за 2 часа. однако когда до пункта с оставалось 6 км, из-за встречного ветра он снизил скорость на 3 км/ч и прибыл в пункт С на 6 минут позже. чем рассчитывал. Чему равна длина маршрута ВС?
Уравнение:
ПРИЛОЖЕНИЕ 2
Задачи для работы в группе
№ 1 Решите задачу на смеси:
После смешения двух растворов, один из которых содержит 48 г, а другой 20 г безводного йодистого калия, получилось 200 г нового раствора. Найдите концентрацию каждого из первоначальных растворов. если концентрация первого на 15% больше второго.
Справочная информация:
Концентрация - доля чистого вещества в смеси

№ 2
1. Решите задачу, составляя рациональное уравнение
Две старушки вышли одновременно навстречу друг другу из двух городов. Они встретились в полдень и достигли чужого города: первая в 4 ч по полудни, а вторая - в 9 ч. Нужно узнать, когда они вышли из своих городов (обозначьте за х - время до встречи, весь путь примите за 1).
2. Рассмотрите решение задачи с помощью подобия треугольников.
Изобразим график движения старушек и применим метод подобия.
Пусть старушки до встречи шли х ч.
АD - промежуток времени движения первой старушки
СВ - промежуток времени движения второй старушки.
КL - отсекает промежутки времени движения старушек до встречи. На рисунке АL - промежуток времени движения до встречи. S,км
С К 4 D
I
N
II
t,ч
А х L 9 В
Рассмотрите подобие  и
и  ,
, 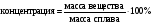 и
и 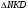 .
.
ПРИЛОЖЕНИЕ 3
Задачи на работу
№1 Профессия - Переводчик
Переводчик должен выполнить художественный перевод 80 страниц текста к определённому сроку. Однако он переводил в день на 2 страницы больше, чем планировал. Поэтому уже за день до срока было переведено на 4 страницы больше. Сколько страниц в день переводил переводчик?
Подсказка 1
Произв-ть, стр./день
Время, дней
Работа. стр.
По плану
Фактически
х
Подсказка 2
Произв-ть, стр./день
Время, дней
Работа. стр.
По плану
х - 2
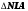
80
Фактически
х
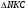
84
Подсказка 3 Уравнение: 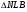
Подсказка 4 Решение уравнения:
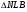 ,
, 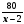
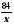
х1=12, х2= - 14 - не удовлетворяет условию задачи,
Ответ: 12 страниц в день переводил переводчик.
№2 Профессия - Секретарь
Одна секретарь может напечатать рукопись на З часа быстрее другой. При совместной работе им потребовалось бы затратить на перепечатку рукописи 6 ч 40 мин. Сколько времени потребуется каждой машинистке, чтобы перепечатать рукопись, работая отдельно?
Подсказка 1
Произв-ть, стр./ч
Время, ч
Работа. стр.
1 секретарь
х
1
2 секретарь
1
вместе
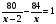
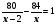
1
Подсказка 2
Произв-ть, стр./ч
Время, ч
Работа. стр.
1 секретарь
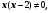
х
1
2 секретарь
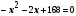
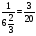
1
вместе
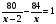
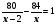
1
Подсказка 3 Уравнение: 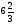
Подсказка 4 Решение уравнения:
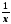 ,
, 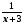
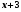
Ответ: 12 часов, 15 часов.
Задачи на работу
№3 Профессия - Экономист в легкой промышленности
Две мастерские должны были пошить по 96 курток. Первая мастерская шила в день на 4 куртки больше, чем вторая, и поэтому выполнила заказ на 2 дня раньше. Сколько курток шила в день каждая мастерская?
Подсказка 1
Произв-ть, кур./день
Время, дней
Работа. кур.
1 мастерская
х
96
2 мастерская
96
Подсказка 2
Произв-ть, кур./день
Время, дней
Работа. кур.
1 мастерская
х
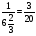
96
2 мастерская
х - 4
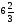
96
Подсказка 3 Уравнение: 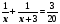
Подсказка 4 Решение уравнения:
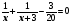 ,
, 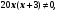
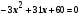
х1=16, х2= - 12 - не удовлетворяет условию задачи,
16 - 4 = 12.
Ответ: 16 курток, 12 курток.
№4 Профессия - Экономист в сельском хозяйстве
Два комбайна убрали поле за 4 дня. За сколько дней мог убрать поле каждый комбайн, если одному из них для выполнения этой работы потребовалось бы на 6 дней меньше, чем другому?
Подсказка 1
Произв-ть, поля в день
Время, дней
Работа
1 комбайн
х
1
2 комбайн
1
вместе
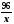
4
1
Подсказка 2
Произв-ть, поля в день
Время, дней
Работа
1 комбайн
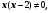
х
1
2 комбайн
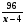
х - 6
1
вместе
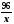
4
1
Подсказка 3 Уравнение: 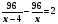
Подсказка 4 Решение уравнения:
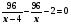 ,
, 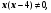
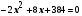
х1=12, х2= 2 - не удовлетворяет условию задачи
Ответ: 12 дней, 6 дней.