Урок Координатно-векторный метод решения стереометрометрических задач

КУРАГИНСКАЯ СОШ № 7

</<br>

РЕШЕНИЕ ЗАДАЧ ПО СТЕРЕОМЕТРИИ

КООРДИНАТНО- ВЕКТОРНЫМ МЕТОДОМ

УЧИТЕЛЬ МАТЕМАТИКИ

ЧЕРВОНЕНКО ТАМАРА ЯКОВЛЕВНА

П. КУРАГИНО 2016 г.

Алгебра - не что иное как записанная

в символах геометрия,

а геометрия - это просто алгебра,

воплощенная в фигурах.

Софий Жермен (1776-1831)

Большую роль в развитии геометрии сыграло применение алгебры к изучению свойств геометрических фигур, разросшееся в самостоятельную науку- аналитическую геометрию. Возникновение аналитической геометрии связано с открытием метода координат, являющегося основным методом. Метод координат - весьма эффективный и универсальный способ нахождения любых углов или расстояний между стереометрическими объектами в пространстве. Рене Декарт является одним из создателей аналитической геометрии . Предложенная им система получила его имя. В геометрии применяются различные методы решения задач. В своей работе я показала решение одной из задач тремя методами. Координатный метод решения задач на сегодняшний день самый мощный и позволяет решить почти все виды математических и не только задач.

АЛГОРИТМ ПРИМЕНЕНИЯ МЕТОДА КООРДИНАТ К РЕШЕНИЮ ГЕОМЕТРИЧЕСКИХ ЗАЧАЧ СВОДИТСЯ К СЛЕДУЮЩЕМУ

1. Выбираем в пространстве систему координат из соображений удобства выражения координат и наглядности изображения.

2. Находим координаты необходимых для нас точек.

3. Решаем задачу, используя основные задачи метода координат.

4. Переходим от аналитических соотношений к геометрическим.

I.Основные формулы:

1.Расстояние между точками А(, ),В, ) равно =.

2.Угол между плоскостями. Если β-угол между плоскостями, заданными уравнениями х+z+ =0 и х+z+ =0, то

.

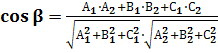
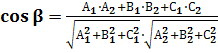3.Расстояние от точки до плоскости. Если ρ- расстояние от точки (, ), до плоскости х+z+D =0,то

ρ=.

4.Уравнение плоскости, проходящей через три заданные точки(, ),(, ),(, ), в координатной форме:

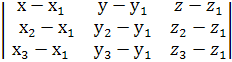
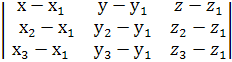=0;

5. Если отрезок, концами которого служат точки А(, ),В, ) разделен точкой С(х, у,) в отношении λ, то координаты точки С определяются по формулам

Х = ; у= ; z=.

Расстояние между скрещивающимися прямыми

Задание 14 (вариант 13 ЕГЭ, Ф. Ф. Лысенко) [5]

В кубе ABCDA₁B₁C₁D₁, ребро которого равно 4, точка M является серединой отрезка BC₁.

а) Постройте сечение куба плоскостью, проходящей через прямую АМ, параллельную прямой А₁В.

б) Найдите расстояние между прямыми А₁В и АМ

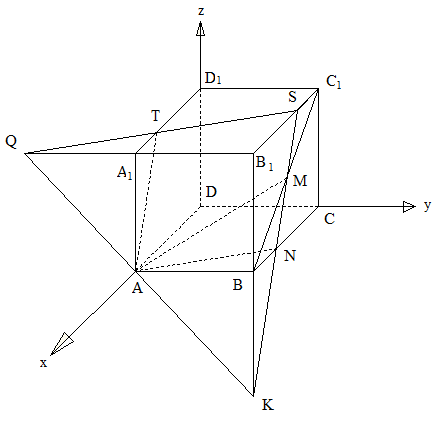
а) В плоскости грани АА1В1В через точку А проведем прямую, параллельную А1В. Q и K- точки пересечения этой прямой соответственно с прямыми А1В1 и ВВ1. Прямая КМ пересекает ребро ВС в точке N, а ребро B1C1 - в точке S. Отрезок SQ пересекает ребро

A₁ D₁ в точке Т.

Четырехугольник ATSN образует искомое сечение, так как все его вершины лежат в плоскости QSK, которая проходит через АМ и прямую АК, параллельную А₁В и, следовательно, (QSK)││ А₁В.

б) Введем систему координат. Ребро куба равно 4. Значит координаты точек:

А(4;0;0); М(2;4;2); К(4;4;-4); А₁(4;0;4); В(4;4;0)

АМ лежит в плоскости сечения, которое параллельно прямой А₁В. Значит за расстояние между прямыми А₁В и АМ можно взять расстояние от любой точки, лежащей на А₁В до плоскости сечения. Составим уравнение плоскости АМК: А(4;0;0); М(2;4;2); К(4;4;-4)

Уравнение плоскости ax+by+cz+d=0

Подставим координаты точек А, М и К в общее уравнение плоскости.

→

Отсюда уравнение плоскости имеет вид

x │

3x+y+z-12=0 Отсюда {3;1;1} нормальный вектор плоскости.

Найдем расстояние

(А₁В, АМ)= == (Формула расстояния от точки до плоскости) [2]

Расстояние от точки до плоскости

(Работа ЕГЭ, математика 2013)

Задача

В правильной треугольной призме АВСА₁В₁С₁ стороны основания равны 2, боковые ребра равны 1, точка D - середина ребра СС₁. Найдите расстояние от вершины С до плоскости ADB₁

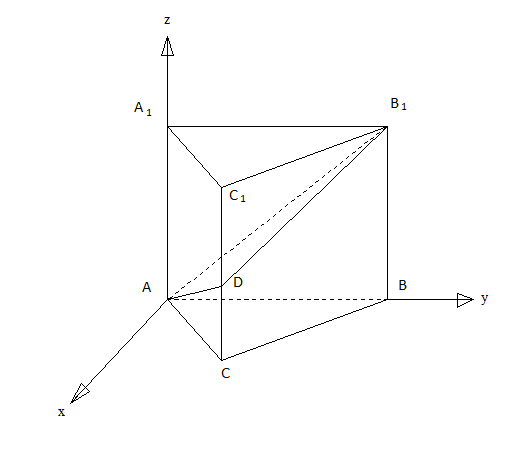
Введем систему координат. Тогда

А (0;0;0) В (0;2;1)

D (;1;0,5) С (;1;0)

Уравнение плоскости, проходящей через 3 заданные точки А (0;0;0), D (;1;0,5) и

В (0;2;1) в координатной форме имеет вид: = 0 [3]

= = 0

Или x+2z-x-y=0

-y+2z=0

y-2z=0 в этом уравнении

ax+bx+cz+d=0

a=d=0

b=

c=-2

{0; нормальный вектор плоскости.

Расстояние находим по формуле из учебника Л. С. Атанасян «Геометрия 10-11» [2]

ρ=(C, ADB₁) = , где C (;C (;

ρ=(C, ADB₁) = = = = =

Расстояние от точки до плоскости

Задание С2 (ЕГЭ 2013, И. В. Ященко) [6]

Радиус основания конуса равен 9, а его высота 12. Плоскость сечения конуса содержит его вершину и хорду основания, длина которой равна 10. Найдите расстояние от центра основания конуса до плоскости сечения.

Эту задачу я решил тремя вариантами чтобы сравнить возможности координатно-векторного метода с другими.

Вариант 1.

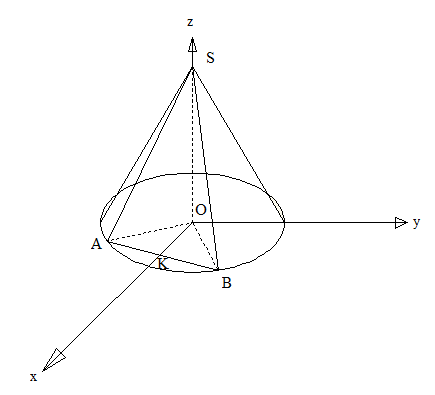
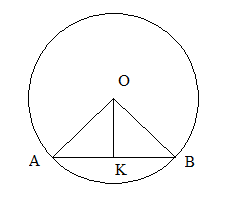
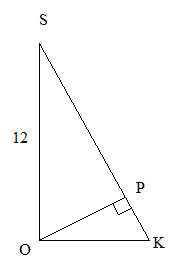
ОК====2;

SK===10

=10*SP

SP===;

ОР²=SP*PK=

ОР=

Вариант2

Рассмотрим объем пирамиды OASB

V_OASB=S_AOB*OS=**10*2*12=

S_OASB=S_ASB*OP

S_ASB*OP=*OP=

OP=

Вариант 3 (координатно-векторный метод)

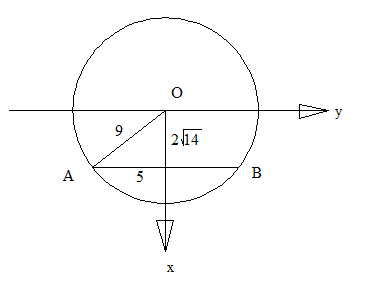
Введем систему координат

А(-5;2;0); В(5; 2

Найдем уравнение плоскости ABS. Общее уравнение имеет вид: ax+by+cz+d=0

Следовательно уравнение плоскости: 0x -

+-1=0

O(0;0;0) найдем расстояние [2]

ρ(0;ABS)=

Угол между плоскостями

Задание 14 (ЕГЭ 2016, Ф.Ф. Лысенко, вариант 31) [5]

В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все рёбра равны 4.

а) Докажите что угол между прямыми AD₁ и DC₁ равен 90^о;

б) Найдите угол между плоскостями FAC₁ и AA₁D

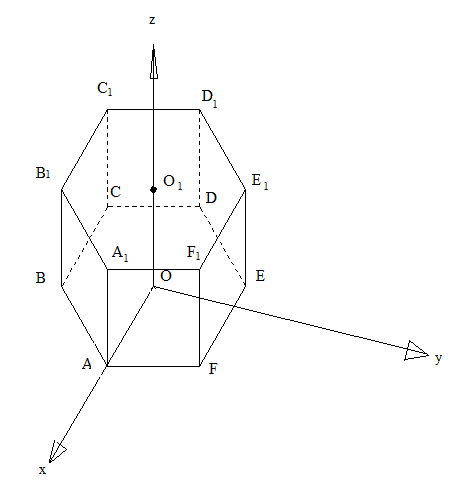
Введем систему координат, тогда точки будут иметь координаты:

A(4;0;0); D(-4;0;0); D₁(-4;0;4); C₁(-2;-2;4)

₁{-8;0;4}; ₁{2;2;4}

₁*₁=-16+16=0

Скалярное произведение векторов равно 0, следовательно вектора перпендикулярны

AD₁ ⊥ DC₁, а значит угол равен 90^о

б) Найдем угол между плоскостями FAC₁ и AA₁D

Составим уравнения плоскостей ax+by+cz+d=0 - общее уравнение плоскости

F(2;2;0); A(4;0;0); C₁(-2;-2;4)

2a+2b+0c+d=0

4a +d=0

-2a-2b+4c+d=0

₁{;нормальный вектор плоскости FAC_1.

Составим уравнение плоскости AA₁D [2]

A(4;0;0); A₁(4;0;4); D(-4;0;0)

a=d=0; с=0; b-любое, пусть b=1. Уравнение y=0.

₂{0;1;0}-нормальный вектор плоскости AA₁D

====

Угол =arccos

Угол между прямыми

Задание 14 ( Вариант 7 ЕГЭ, Ф.Ф. Лысенко) [5]

В основании четырехугольной пирамиды SABCD лежит прямоугольник со сторонами AB=8, BC=15. Боковые ребра SB=6, SC=3, SA=2.

а) Докажите, что SB - высота пирамиды.

б) Найдите угол между SD и AC.

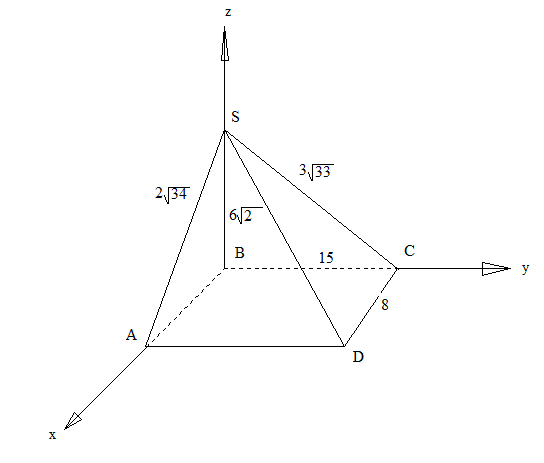
SB плоскости ABCD т.к. SB BC и SB AB

9*33=225+72 верно

136=64+72 верно

Следовательно SB-высота.

б) Введем систему координат A(8;0;0); С(0;15;0); D(8;15;0); S(0;0; 6)

{-8;15;0}, {8;15;- 6}

== [2]

Отсюда =

Площадь сечения.

Задание 14. (Вариант 20 Лысенко 2016) [5]

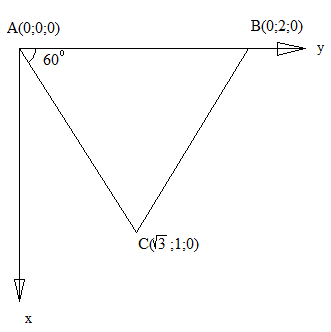
Сторона основания правильной шестиугольной пирамиды SABCDEF равна 6. Боковое ребро наклонено к основанию под углом 60˚. Через меньшую диагональ основания АС проведено сечение, которое пересекает высоту пирамиды в точке, удаленной от основания на расстояние .

а) Докажите что это сечение перпендикулярно противоположному к АС боковому ребру пирамиды SE.

б) Найдите площадь сечения.

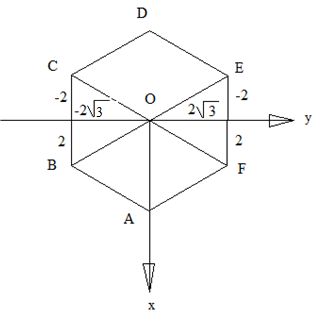
Введем систему координат: ось ОХ т О и середина AF, ось OY-OE

Построим сечение: АС разделим пополам - точка М.

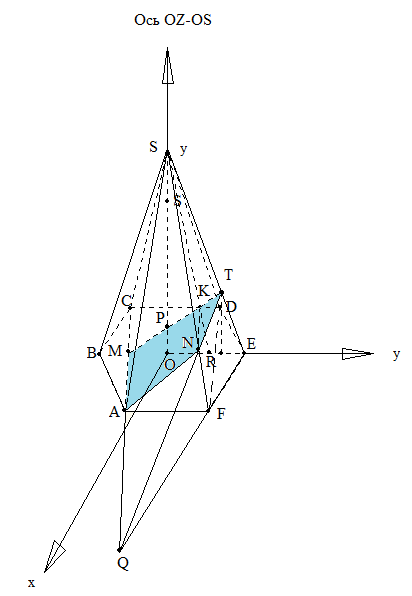
На OS отложим ОР= и соединим МР до пересечения с SE в точке Т, точка К - лежит на SR, где R середина ОЕ. Продолжим АС и FE точка Q, соединим Q c T, точка N точка пересечения QT и SF.

Координаты точек: S(0;0;6); Е(0;6;0); Р(0;0;); М(0;-3;0). Тогда {0;-3;-}

{0;-6;6}, отсюда *=0+18-18=0, то есть .

А(3;-3;0); C(-3;-3;0); {-6;0;0}; *=0+0+0=0

перпендикулярно двум прямым АС и РМ, которые пересекаются в М и лежат в плоскости сечения. Отсюда перпендикулярно плоскости сечения, что и требовалось доказать.

б) Начертим треугольник OSE. В этом треугольнике SEO=60˚; OS=6; ОЕ=6, значит PS=5, S=30˚; ST=7,5; Т¹Е=2,25

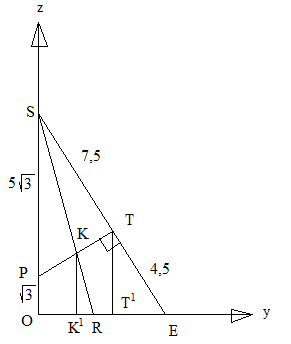
Найдем координаты точки К как точки пересечения прямой МР и SR, PMO=30˚; tgPMO=; отсюда уравнение прямой МР→z=; tgORS==2;

Прямая SR→z=-2y+6

; =; +=; =;

у=; у=; ордината точки К есть

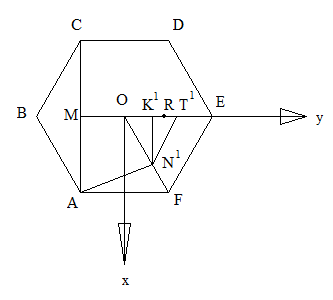
Площадь сечения найдем как площадь проекции МК¹Т¹N¹A, что представляет собой трапецию МК¹N¹А и треугольник К¹Т¹N¹, тогда абсцисса точки К¹ будет

S трапеции=*h; S_МК1_N1_А=*МК¹=;

S∆К¹Т¹N¹=*

½ S проекции сечения=+=

; Тогда площадь половины сечения будет:

:=; где =cos30˚; Откуда площадь всего сечения S=.

Мною рассмотрены ряд разнообразных задач по стереометрии как по нахождению разных величин, так и различных стереометрических тел: призмы, пирамиды, конус. Я просмотрела весь задачник по ЕГЭ 2016 года под редакцией Ф.Ф.Лысенко и постаралась взять из сборника различные задачи. Их решение поможет при подготовке и выполнении ЕГЭ профильного уровня учащимся 11 класса

ИСТОЧНИКИ ИНФОРМАЦИИ

1.Агачев П.Е. Курс высшей математики. Для заочных техникумов.1970, М:, Высшая школа, 539с.

2. Атанасян Л.С., Бутузов В.Ф..Геометрия 10-11,2014,М.: Просвещение,256с.

3. Выгодский М.Я. Справочник по высшей математике. 1973. М:. Наука.,870с.

4..Глаголев Н.А. Элементарная геометрия: стереометрия для 10-11 кл. ср. шк. В 2 ч.-М.: просвещение-ч.2

5..Лысенко Ф.Ф. Математика. Подготовка к ЕГЭ-2016: учебно-методическое пособие.- Ростов-на Дону: Легион-М., 2015 .

6. Ященко И.В. Математика 2012 М.: Астрель 2012-(ФИПИ)

7. Интернет ресурсы:

http: //ru.wikipedia/org/wiki/pi