Урок по алгебре на тему 'Квадратные уравнения' (8 класс)

Открытый урок по алгебре в 8 классе

по теме «Квадратные уравнения»

Цели:

1. Закрепление решений квадратных уравнений.

2. Развитие самостоятельности, творчества, критического мышления.

Задачи:

1. Повторить и обобщить теоретический материал.

2. Развитие вычислительных навыков.

3. Развитие внимательности, самостоятельности, способствовать рациональной организации труда.

Эпиграф: «Знание только тогда знание, когда оно

приобретено усилиями своей мысли, а

не памятью»

Л.Н. Толстой

План урока

1. Организационный момент.

2. Разминка (устная работа).

3. Работа в парах.

4. Работа у доски.

5. Домашнее задание.

6. Рефлексия.

Ход урока

1. Вы уже умеете решать квадратные уравнения. Но знание надо не только иметь, но и надо уметь его показать и применить, что мы и постараемся сегодня сделать на уроке.

а) Составить квадратные уравнения с коэффициентами, заданными в таблице и указать вид уравнения (полное, неполное, приведенное)

№

а

в

с

уравнение

Вид уравнения

1

-2

5

4

2

1

3

0

3

-4

0

1

4

9

0

0

5

1

-5

6

б) Заполнить таблицу

Уравнение

а

в

с

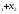
х

х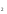∙ х

х, х

х²+ х - 12 = 0

х²-10х + 21= 0

х²-19х + 88 = 0

в) Решить анаграммы ( в словах изменен порядок букв)

1) ИТАИМДКИСНРН (ДИСКРИМИНАНТ)

2) ЭФКОЦИТИФНЕ (КОЭФФИЦИЕНТ)

3) НЕУЕАРВНИ (УРАВНЕНИЕ)

Великий, немецкий ученый А. Энштейн говорил о себе «Мне приходится делить свое время между политикой и уравнениями . Однако , уравнения по- моему, гораздо важнее, потому что политика существует только для данного момента, уравнения будут существовать вечно»

Тема «Квадратные уравнения» очень важна в курсе алгебры и является ступенькой в изучении более сложного материала.

2. Работа в парах

а) один из самых молодых и суровых олимпийских видов спорта, корни которого базируются на гонках, проводимых во Франции в 1920-1930 годах «Гонках находчивых»

Решите уравнения, вычеркните из таблицы буквы, соответствующие корням квадратных уравнений. Оставшиеся буквы будут образовывать нужное слово.

0; 4

0; 3

0;-6

1; 2

6; 0

1;-1

1; 3

3;-3

7;0

-7;1

0; 2

6;2

-1;-4

с

т

а

р

и

д

а

к

т

л

у

о

н

(ТРИАТЛОН)

1. х²-4 х = 0

2. х²+7 х = х

3. 5х²-5 = 0

4. х²-9=0

5. 3х² = 6 х

Триатлон- один из самых молодых олимпийских видов. Впервые на

Олимпиадах соревнования по триатлону прошли в Сиднее (Австралия)

в 2000 году. В этих изнурительных состязаниях участникам нужно

преодолеть три упражнения: плавание 1500 м, велосипед 40 км, бег 10

км ,перерывов между дисциплинами не предусмотрено.

б) Назовите один из зимних олимпийских видов спорта, который зародился в Швейцарских Альпах.

Решите уравнения, вычеркните буквы, соответствующие уравнениям, которые не имеют корней.

1. х²-11 х +5= 0 С

2. х²+7 х +30 = 0 М

3. 3х²-14 х +16 = 0 К

4. х²+7 х +3 = 0 Е

5. 2х²-4 х + 9 = 0 Д

6. -4х²-9 х +3 = 0 Л

7. 5х²+8 х - 9 = 0 Е

8. х²+2 х+ 5 = 0 В

9. 7х²-20 х +14 Т

10. 5х²+9 х +4 = 0 О

11. 9х²-30х +25 = 0 Н

Скелетон- спуск по ледяному желобу на двухполозьевых санях. Победитель определяется по сумме двух заездов.

В) кандидат на включение в олимпийские виды спорта, спортивный вид восточных боевых единоборств, признанный в Российской Федерации и других странах мира

1; 10

0; 2

-3; 3

0; 1

(КУДО)

К х²-5=(х - 5) (2 х -1)

Д 2(х²-5)= х²-1

О (х+3)( х-4)=-12

У (х+1) ²=( 2х-1) ²

Кудо включает в себя элементы и приемы каратэ, дзюдо, английского и

тайского бокса, создан в 1981 году.

3. Решение квадратных уравнений с параметром

1. В уравнение х²+рх+35=0 один из корней равен 7. Найти другой корень и коэффициент Р.

2. Один из корней уравнения ах²-3х-5=0 равен 1. Найдите коэффициент а.

4) Рефлексия

Учащимся предлагается ответить на вопросы:

Что понравилось мне сегодня на уроке?

В чем я испытывал затруднения?

Сегодня мне удалось…

Кто может сказать: "Да, я умею решать квадратные уравнения!"

5) Домашнее задание

1-группа Решить уравнения:

х²+5х-24=0

х²-11х+18=0

х²-5х-6=0

х²-4х+4=0

3х²+4х+20=0

5х²-3х-2=0

Вашему вниманию предлагается одна из задач знаменитого индийского XII в. Бхаскары:

«Обезьянок резвых стая,
Всласть поевши, развлекалась.
Часть восьмая их в квадрате
На поляне забавлялась.
А двенадцать по лианам…
Стали прыгать, повисая…
Сколько ж было обезьянок,
Вы скажите, в этой стае?»
Решить с помощью квадратного уравнения.

2-группа - Решить уравнения

3х²-7х+4=0

8х²-14х+5=0

3х²-8х+5=0

3(х-2)²=0

(х+4)²=3х+40