- Учителю
- Урок по алгебре в 10 классе
Урок по алгебре в 10 классе
Конспект урока
Тема: "Показательная функция»
Выполнила
Гаврилова Александра Михайловна
Тема: " Показательная функция".
Класс: 10.
Тип урока: урок формирования новых знаний.
Цели урока:
Обучающие: познакомить учащихся с показательными функциями; дать представление о показательных функциях; научить определять виды показательных функций; научить самостоятельно строить и описывать свойства показательных функций.
Развивающие: продолжить развитие умения анализировать, сопоставлять, сравнивать, выделять главное, устанавливать причинно-следственные связи; приводить примеры, формировать умения работы с литературой
Воспитательные: формирование трудолюбия, эстетических навыков при выполнении записей в тетрадях, построении графиков, навыков работы с книгой, вычислительных навыков
образовательные: познакомить;научить чтению и анализу карт, схем; активизировать познавательную активность; раскрыть типичные черты и.т.д.
Оборудование: компьютер, программа Excel, классная доска, презентация, учебник, рабочая тетрадь, чертёжные инструменты.
Литература:
1. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни/ [С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин]. - 8-е изд. - М.: Просвещение, 2009. - 430 с.
2. Алгебра и начала математического анализа. Дидактические материалы. 10 класс: базовый и профил. уровни/ М. К. Потапов, А. В. Шевкин. - 5-е изд. - М.: Просвещение, 2011. - 159 с.
План
-
организационный (2 мин);
-
сообщение темы урока (2 мин);
-
изложение нового материала (15 мин);
-
решение задач (19 мин);
-
подведение итогов обучения (5 мин);
-
домашнее задание и его инструктаж (2 мин).
Ход урока
№ п/п
Действия учителя
Действия ученика
Методы обучения
Средства обучения
Форма организации учебной деятельности
1
Заходит в класс, приветствует учеников.
Приветствуют учителя
2
На прошлом уроке мы с вами изучили степень с иррациональным показателем. Тетради с домашней работой вы мне сдали, поэтому я их проверю и выставлю за них оценки. Сегодня на уроке мы познакомимся с новым видом функций, а именно с показательными функциями. Открываем тетради, записываем число, классная работа, тема: "Показательные функции"
Открывают тетради, записывают число, классная работа и тема урока: "Показательные функции"
3
(слайд 1) Функция - основной математический инструмент для изучения связей, зависимостей между различными величинами. Чем большим запасом функций мы располагаем, тем шире и богаче наши возможности математического описания окружающего мира. Какие функции вам известны?
Какие свойства функций вам известны?
(слайд 2, 3) Рассмотрим графики некоторых функций и определим для них значения этих свойств.
(слайд 4) Ученые-биологи, изучая жизнь бактерий, установили, что рост числа бактерий происходит по формуле N=5t, где N-число колоний бактерий в момент времени t, t- время размножения.
(слайд 5) Вычислите, как изменится число колоний бактерий за 2 секунды?
За 3 секунды?
Т.е. каждому моменту времени соответствует свое определенное число бактерий.
Зависимость такого типа между двумя переменными была замечена не только в процессе роста числа микроорганизмов, но и, например, в спорте - зависимость длины прыжка спортсмена с трамплина от начальной скорости полета.
Для зависимостей данного вида составлена следующая математическая модель: y = ax.
Я предлагаю вам сегодня на уроке исследовать эту математическую модель. Что значит "изучить функцию"?
(слайд 6) Функция y = ax с основанием а > 0, а ![]() 1 называется показательной функцией с основанием а. Приведите примеры показательных функций. (Названные учениками примеры записать на доске). Эта функция обладает одним замечательным свойством: скорость роста пропорциональна значению самой функции.
1 называется показательной функцией с основанием а. Приведите примеры показательных функций. (Названные учениками примеры записать на доске). Эта функция обладает одним замечательным свойством: скорость роста пропорциональна значению самой функции.
Какие значения может принимать основание показательной функции?
Почему на основание функции наложены такие ограничения?
(слайд 7) Итак, чтобы исследовать свойства показательной функции, построим графики этой функции при различных основаниях с помощью приложения Excel. Причем, отдельно будем рассматривать функции с основанием в виде правильной дроби, отдельно - с основанием в виде неправильной дроби. Займите компьютеры. Результаты ваших исследований запишите в таблицу ().
(слайд 8) 1. Область определения
2. Множество значений
3. Пересечение с осью OY
4. Монотонность
(слайд 9) 1. Область определения
2. Множество значений
3. Пересечение с осью OY
4. Монотонность
Теперь сделаем вывод по проделанной работе и составим таблицу (слайд 10)
Линейная функция, описывает, например, равномерное прямолинейное движение; Квадратичная функция - описывает движение с ускорением;
Обратная пропорциональность - описывает, например, зависимость объема, занимаемого газом, от его плотности.
-
Область определения
-
Множество значений
-
Точки пересечения графика с осями координат
-
Промежутки монотонности
(проверяют свойства по презентации)
Увеличится до 25.
Увеличится до 125.
Изучить функцию, значит, дать ее определение, рассмотреть свойства и построить график. Это и есть цели нашего сегодняшнего урока.
а > 0, а ![]() 1
1
Пусть а < 0. Чему равно (-7)1/2? - не имеет смысла
Пусть а = 0. Чему равно 00? - не имеет смысла
Пусть а = 1, Чему равно 1х? =1 - константа
Поэтому, основание показательной функции а > 0, а ![]() 1.
1.
(выполняют работу)
y = ax , а > 1
x ![]() (-
(-![]() ;+
;+![]() )
)
y ![]() (0;+
(0;+![]() )
)
(0;1)
Возрастает на всей области определения
0
x ![]() (-
(-![]() ;+
;+![]() )
)
y ![]() (0;+
(0;+![]() )
)
(0;1)
Убывает на всей области определения
Опрос
Объяснение
Исследо
вание
Презента
ция
Excel, прило
жение 2
Презента
ция
Фронталь
ная
Индиви
дуальная
4
Свойство монотонности показательной функции используется при решении многих задач. Например: 1) Сравнить числа, 15-2 и 152 .
2) Сравнить числа 0,4-2 и 0,42.
Я предлагаю вам выполнить несколько заданий, чтобы проверить, как вы усвоили новый материал (приложение 3). С последующей проверкой
Критерии оценок:
"5" - 5 правильных ответов;
"4" - 3 - 4 правильных ответа;
"3" - 2 правильных ответа.
(слайд 11 с ответами)
Рассмотрим функцию у = 15х, т.к. основание 15 > 1, то функция монотонно возрастает, сравниваем показатели: - 2 < 2, значит, 15-2 < 152.
Т.к. функция у = 0,4х убывает и -2 < 2, то 0,4-2 > 0,42.
Решение задач
Приложе
ние 3, презента
ция
Индивидуаль
ная
5
Какая функция называется показательной?
Назовите свойства показательной функции для а > 1 и 0
Какие свойства функции являются общими для этих двух случаев?
Функция y = ax с основанием а > 0, а ![]() 1 называется показательной функцией с основанием а.
1 называется показательной функцией с основанием а.
0
a>1
1. Область определения
x Î(-∞;+∞)
x Î (-∞;+∞)
2. Множество значений
y Î(0;+∞)
y Î(0;+∞)
3.Пересечение с осью OY
(0;1)
(0;1)
4. Монотонность
убывает
на всей области определения
возрастает
на всей области определения
Область определения и значения, пересечение с осью OY
Опрос
Фронталь
ная
6
Дома вам надо изучить самостоятельно пункт 4.8. № 4.60 и задание на карточке (приложение 2). (прощается с учениками)
(записывают задание в дневники, прощаются с учителем)
Приложение 1
1. Запустите программу Excel
2. На Листе 1 постройте в одной системе координат графики функций у=2х , у=3х , у=4х ,
хÎ[-2; 2], шаг 0,5. Измените цену деления оси ОУ: пкм - формат оси - шкала - цена основных делений 1.
3. На Листе 2 постройте в одной системе координат графики функций у=(1/2)х , у=(1/3)х , у=(1/4)х , хÎ[-2; 2], шаг 0,5. Измените цену деления оси ОУ: пкм - формат оси - шкала - цена основных делений 1.
4. Исследуйте свойства функции у=ах при а > 0 и 0< а <1. Результаты исследования запишите в таблицу
Свойства функции.
![]()
![]()
1. Область определения
2. Множество значений
3. Пересечение с осью OY
4. Монотонность
Приложение 2
Решение домашнего задания
1. Упростите выражение ![]()
![]()
![]()
Ответ. 0.
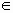
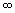
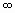
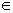
Приложение 3.