Пробный экзамен по математике ЕГЭ ( профильный)

1. Флакон шампуня стоит 160 рублей. Какое наибольшее количество флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25%?

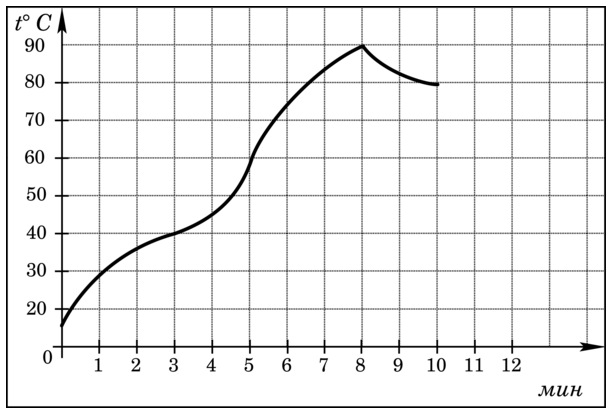
2. На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее с момента запуска двигателя, на оси ординат - температура двигателя в градусах Цельсия. Определите по графику, сколько минут двигатель нагревался от температуры до температуры .

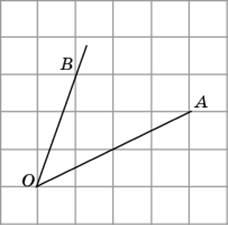
3. На клетчатой бумаге с размером клетки 1 x 1 изображён угол BOA. Найдите тангенс этого угла.

4. Фабрика выпускает сумки. В среднем 3 сумки из 25 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов.

5. Найдите корень уравнения .

6. В прямоугольном треугольнике АВС угол С равен , AB = 4, . Найдите АС.

7. Прямая является касательной к графику функции . Найдите абсциссу точки касания.

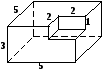
8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

9. Найдите значение выражения .

10. Трактор тащит сани с силой кН, направленной под острым углом к горизонту. Работа трактора (в килоджоулях) на участке длиной м вычисляется по формуле . При каком максимальном угле (в градусах) совершенная работа будет не менее 2000 кДж?

11. Первый и второй насосы наполняют бассейн за 9 минут, второй и третий - за 14 минут, а первый и третий - за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?

12. Найдите наименьшее значение функции на отрезке .

13. а) Решите уравнение .

б) Найдите все корни этого уравнения, принадлежащие отрезку .

14. В правильной четырехугольной призме ABCDA₁B₁C₁D₁ точка K делит боковое ребро AA₁ в отношении AK:KA₁ = 1:2. Через точки B и K проведена плоскость , параллельная прямой AC и пересекающая ребро DD₁ в точке M.

а) Докажите, что плоскость делит ребро DD₁ в отношении DM:MD₁ = 2:1.

б) Найдите площадь сечения, если известно, что , .

15. Решите неравенство .

16. Окружность, вписанная в треугольник KLM, касается сторон KL, LM и MK в точках A, B и C соответственно.

а) Докажите, что .

б) Найдите отношение LB:BM, если известно, что и .

17. Вася мечтает о собственной квартире, которая стоит 3 млн.руб. Вася может купить ее в кредит, при этом банк готов выдать эту сумму сразу, а погашать кредит Васе придется 20 лет равными ежемесячными платежами, при этом ему придется выплатить сумму, на 180% превышающую исходную. Вместо этого, Вася может какое-то время снимать квартиру (стоимость аренды ― 15 тыс. руб. в месяц), откладывая каждый месяц на покупку квартиры сумму, которая останется от его возможного платежа банку (по первой схеме) после уплаты арендной платы за съемную квартиру. За какое время в этом случае Вася сможет накопить на квартиру, если считать, что стоимость ее не изменится?

18. Найдите все такие значения параметра , при каждом из которых наименьшее значение функции меньше 2.

19. После того, как учитель доказал классу новую теорему, выяснилось, что большая часть класса не поняла доказательство. На перемене один ученик вдруг понял доказательство (и только он). Также известно, что в классе учится не более 30, но не менее 20 человек.

а) Могло ли получиться так, что теперь уже меньшая часть класса не понимает доказательство?

б) Могло ли получиться так, что исходно процент учеников, понявших доказательство, выражался целым числом, а после перемены ― нецелым числом?

в) Какое наибольшее целое значение может принять процент учеников класса, так и не понявших доказательство этой теоремы?