- Учителю
- МЕТОДИЧЕСКАЯ РАЗРАБОТКА 'РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ'
МЕТОДИЧЕСКАЯ РАЗРАБОТКА 'РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ'
ГБПОУ "КЛТ"
Методическая разработка для обучающихся I курса
по теме "Решение тригонометрических уравнений"
по дисциплине математика
Преподаватель Дзюба Л.Г.
2015
Арксинусом числа а и обозначают arcsin a: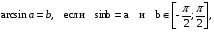 при этом
при этом
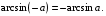
Пример: 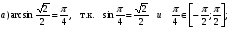
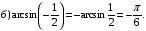
Арккосинус 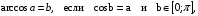 при этом
при этом
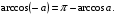
Арктангенс 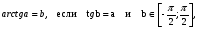 при этом
при этом
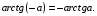
Арккотангенс 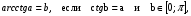 при этом
при этом
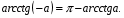
Примеры:
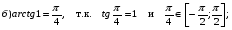
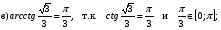
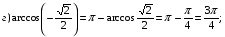
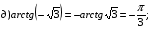
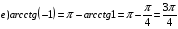 .
.
№ 1. Вычислите:
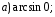
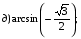

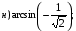
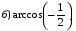
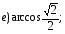
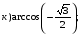

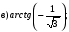
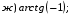

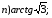
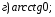
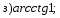
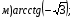
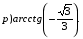
№ 2. Найдите значение выражения:
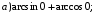

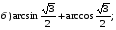
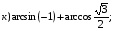
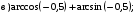
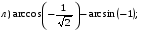
Таблица значений тригонометрических функций
Значения тригонометрических функций можно определять по таблицам М.В. Брадиса, но в тригонометрии чаще используются углы, содержащиеся в следующей таблице: Заметим, что 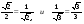
nо
0о
30о
45о
60о
90о
120о
135о
150о
180о
210о
225о
240о
270о
300о
315о
330о
360о
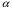
0
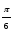
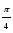
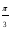


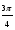
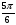
π
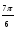
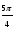

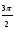
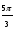
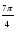
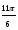
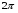
sin α
0
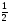
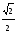
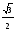
1
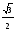
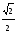
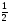
0
-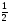


-1


-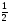
0
cos α
1
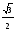
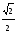
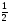
0
-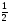


-1


-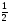
0
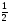
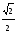
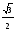
1
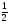
0

1

-
-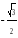
-1
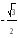
0

1

-
-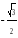
-1
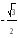
0
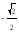
-

1

0
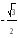
-1
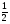
-
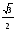
1

0
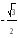
-1
-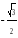
-
Урав-нение
Решение
Частные случаи
Примечания
sinx=a
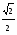
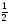
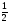
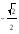

cosx=a
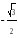
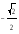
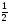
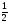

tgx=a
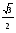
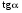

ctgx=a
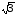
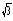
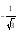
При решении простейших тригонометрических уравнений удобнее пользоваться стандартными формулами:
Пример: Решите уравнение:
 Ответ:
Ответ:  .
.
б)
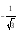
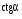 ;
;  Ответ:
Ответ: 
в)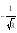
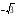
 Ответ:
Ответ: 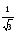
г)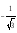
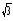
 Ответ:
Ответ: 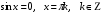
д)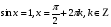 Преобразуем выражение
Преобразуем выражение
2 ;
; 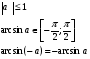
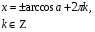
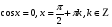 Ответ:
Ответ: 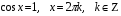
е)
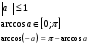
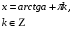
 Ответ:
Ответ: 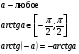
ж) , т.к. аргумент у косинуса - сложная функция, то уравнение решают сначала относительно
, т.к. аргумент у косинуса - сложная функция, то уравнение решают сначала относительно  , а затем выражают
, а затем выражают 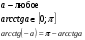 .
.
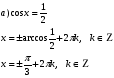
![]()

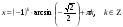 Ответ:
Ответ: 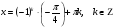
з)
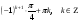
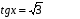

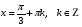 Ответ:
Ответ: 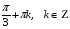
№ 3. Решите уравнение:

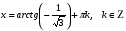



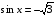

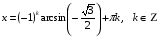

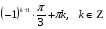
№ 4. Решите уравнение:
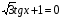
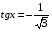
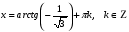

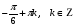
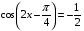
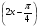

№ 5. Решите уравнение:
а)

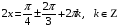


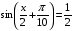
№ 6. Решите уравнение:

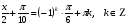
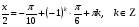


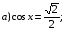
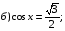
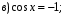
Методы решения тригонометрических уравнений
Заметим, что каково бы ни было заданное тригонометрическое уравнение, существует только четыре вида уравнений, дающие решения - это простейшие тригонометрические уравнения.
Рассмотрим основные методы решения тригонометрических уравнений, позволяющие сводить их к простейшим.
-
Упрощение уравнения, используя тригонометрические формулы.
Пример 1. Решите уравнение: 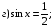
Преобразуем выражение и воспользуемся формулой 
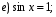

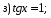 ;
;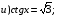 - простейшее тригонометрическое уравнение
- простейшее тригонометрическое уравнение
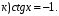 ;
; 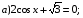
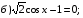 Ответ:
Ответ: 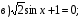
Пример 2. Решите уравнение: 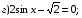
Используем Формулы приведения 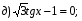 ;
; 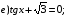
Пример 3. Решите уравнение: 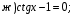

Пример 4. Решите уравнение: 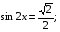

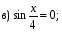
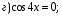
Ответ: 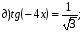 ;
; 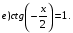 .
.
Пример 5. Решите уравнение: 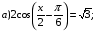 Используя формулы приведения заменим
Используя формулы приведения заменим  :
: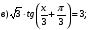
представим выражение в виде произведения:
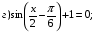
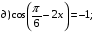 ;
; 
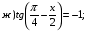 ;
;  Ответ:
Ответ: 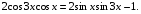
Пример 6. Решите уравнение: 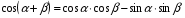
Используя формулу (1) п. 6, заменим 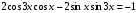 на 1.
на 1.
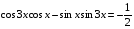 Ответ:
Ответ: 
Пример 7. Решите уравнение: 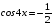
Сгруппируем слагаемые так, чтобы получились формулы: суммы и двойного аргумента.
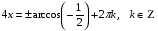
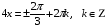 ;
; 
Вынеся 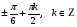 общим множителем, получим два простейших уравнения:
общим множителем, получим два простейших уравнения:
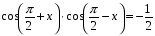
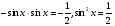
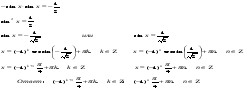


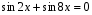
Ответ: 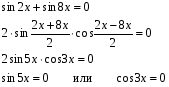 ;
; 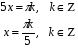 .
.
II. Метод введения новой переменной
Очень часто тригонометрическое уравнение по внешнему виду напоминает квадратное уравнение. Выполнив в уравнении соответствующую замену переменной, можно легко найти его решение.
Пример 8. Решите уравнение: 
Замена 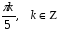

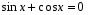
Обратная замена: 
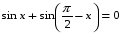
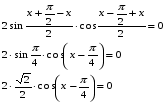
Ответ: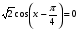 ;
; 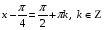 .
.
В некоторых уравнениях требуется сделать дополнительное преобразование, чтобы уравнение свелось к квадратному:
Пример 9. Решите уравнение: 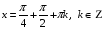
Заменим, , 
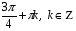
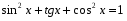 Замена:
Замена: 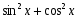
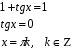 Решив уравнение, найдем
Решив уравнение, найдем 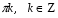 Обратная замена:
Обратная замена: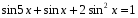 - уравнение не имеет решения,
- уравнение не имеет решения,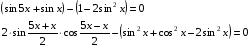 т.к.
т.к. 
Ответ: 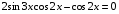 .
.
Пример 10. Решите уравнение: 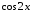
Заменим  , и выполним домножение обеих частей
, и выполним домножение обеих частей
уравнения на  . Учитывая, что
. Учитывая, что  , имеем:
, имеем:

 Замена:
Замена: 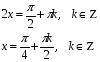
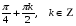 .
.
 Обратная замена:
Обратная замена:
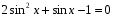
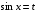
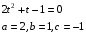
Ответ: 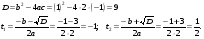 ;
; 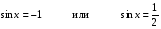 .
.
III. Однородные тригонометрические уравнения.
Однородные тригонометрические уравнения разделяются на два вида:
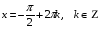 - однородное уравнение первой степени;
- однородное уравнение первой степени;
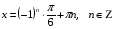 - однородное уравнение второй степени.
- однородное уравнение второй степени.
Разделив обе части уравнения а) на cosx; б) на 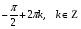 , с учетом, что
, с учетом, что 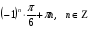 , получим уравнения:
, получим уравнения:
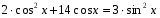 - простейшее;
- простейшее;
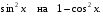 - квадратное.
- квадратное.
Рассмотрим несколько решений однородных уравнений:
Пример 11. Решите уравнение: 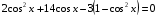
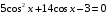 ;
; 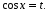

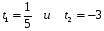 Ответ:
Ответ:  .
.
Пример 12. Решите уравнение: 
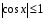
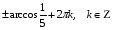 Решив это уравнение, получим:
Решив это уравнение, получим:
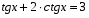

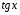
Ответ: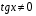 ;
; 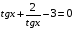 .
.
Если в однородном уравнении второй степени присутствует свободный член 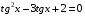 , то его можно заменить:
, то его можно заменить: 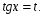 .
.
Пример 13. Решите уравнение: 

 , откуда
, откуда 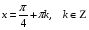 ,
,
т.е. 

Ответ: 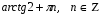 ;
;  .
.
Рассмотренные в данном пункте методы решения тригонометрических уравнений являются базовыми и обязательны к изучению.
№ 7. Решите уравнение:
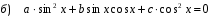
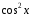

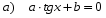
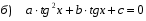
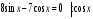

№ 8. Решите уравнение  и найдите сумму его решений на отрезке
и найдите сумму его решений на отрезке 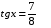
№ 9. Найдите (в градусах) все решения уравнения  , удовлетворяющие условию
, удовлетворяющие условию 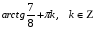 .
.
№ 10. Решите уравнение:
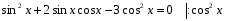
№ 11. Решите уравнение:

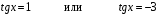
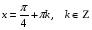

№12. Найдите все решения уравнения 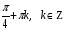 принадлежащие отрезку
принадлежащие отрезку  .
.
№ 13. Упростите выражение 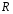 и укажите х, при которых его значение равно
и укажите х, при которых его значение равно 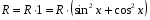
№14. Решите уравнение:
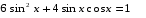

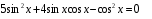

№ 15. Найдите все решения уравнения 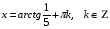 , лежащие в интервале
, лежащие в интервале 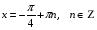
№ 16. Решите уравнение: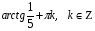 ;
;
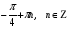 ;
;
 ;
;

№ 17. Решите уравнение:
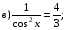
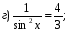
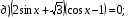

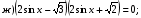
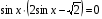
№ 18. Решите уравнение:
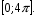

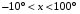
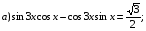
№19. Решите уравнение: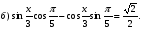
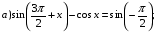
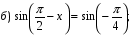

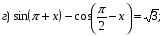

Практическое занятие Тема: Решение тригонометрических уравнений.
Цель занятия : изучить приемы и методы решения различных тригонометрических уравнений .
Задание 1. Решите уравнения:
1) 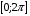 ; 2)
; 2) 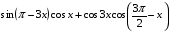 ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 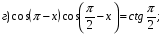 ; 6)
; 6) 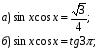
7) 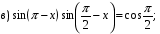 ; 8)
; 8) 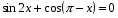 ; 9)
; 9)![]() 10)
10) 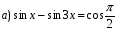 11)
11) ![]()
12)![]() 13)
13) 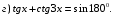 ; 14)
; 14)  ; 15)
; 15)  ; 16)
; 16) 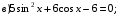 ;
;
17) ![]() 18)
18) ![]() 19)
19)![]() 20)
20)![]() 21)
21)![]()
22)![]() 23)
23)![]() 24)
24)![]() 25)
25) 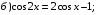 26)
26) 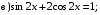 27)
27) 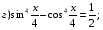
28) tg 2x=0 29) tg (x-1)= 1 30) 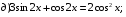 31)
31)  32)
32) 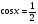
Задание 2. Решить уравнение, используя метод замены переменной и сводя его к квадратному :
1) 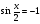 ; 2)
; 2) 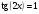 ; 3)
; 3) 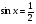 ;
;
4) 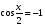 ; 5)
; 5) 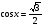 ; 6)
; 6) ; 7)
; 7)  ;
;
8)  ; 9)
; 9) 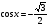 ; 10)
; 10)  ;
;
11)  12)
12)  ; 13)
; 13) 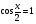 ; 14)
; 14) 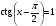 ; 15)
; 15) 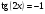

25)  26)
26)  27)
27) 
27)  28)
28)  29)
29) 
30)  31)
31) 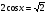 32)
32) 
3. Решить уравнение методом разложения на множители:
1) 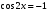 ; 2)
; 2) 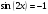 ; 3)
; 3)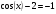 4)
4)  ;
;
5) 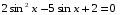 6)
6)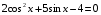 ; 7)
; 7) 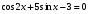
 17)
17)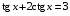 18)
18) 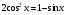
20) 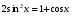 ; 22)
; 22) 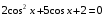 ; 23)
; 23) 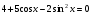
24) 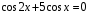 ;25)
;25)  ; 26)
; 26) 
27) 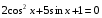 ; 28)
; 28) 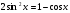 ;29)
;29) 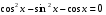 ; 30)
; 30) 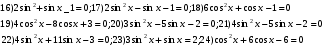
31)  32)
32) 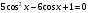
4. Решите уравнение, используя однородность:
1) 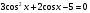 ; 2)
; 2)  ; 3)
; 3) 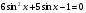 ;
;
4) 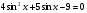 ;5)
;5) 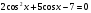 ;
;
6)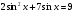 7)
7) ; 8)
; 8) 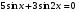 ;
;
9) 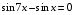 ;10)
;10) 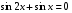 11)
11)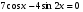 ; 12)
; 12) 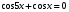 ;13)
;13) 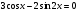 14)
14) 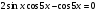 ; 15)
; 15)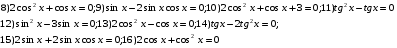 ; 16)
; 16) 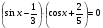 ; 17)
; 17)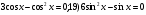
18) 19)
19)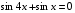 20)3sin2 x - 4sin x cos x + cos2 x = 0
20)3sin2 x - 4sin x cos x + cos2 x = 0
21) sin x = 2 cos x 22) 7cos2 x + 3 sin2x =0 23) 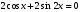 sin x + cos x = 0 24)
sin x + cos x = 0 24) 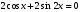 sin 3x - cos 3x = 0
sin 3x - cos 3x = 0
25) 4cos 3x + 5 sin 3x =0 26) 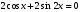 cos2x +sin 2x =0 27)
cos2x +sin 2x =0 27) 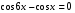
28)  29)
29) 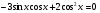 30)
30) 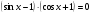
31)  32)
32) 