Практический материал к проведению олимпиады по математике в 9, 10 и 11 классах

Задания районного этапа олимпиады

школьников по математике

2013-2014 учебный год

11 класс

1. Доказать, что, если а, в, с - положительные числа, то .

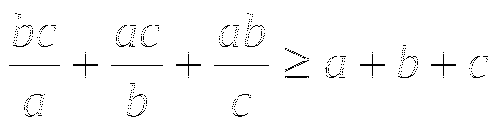(5 баллов)

2. Решите уравнение: .

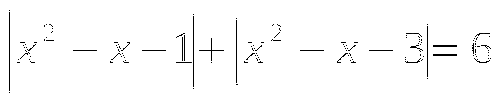(7 баллов)

3. Непараллельные стороны трапеции продолжены до взаимного пересечения и через полученную точку проведена прямая, параллельная основаниям трапеции, Найти отрезок её, ограниченный продолжениями диагоналей, если основания равны а и в (а>в).

(10 баллов)

4. Известно, что 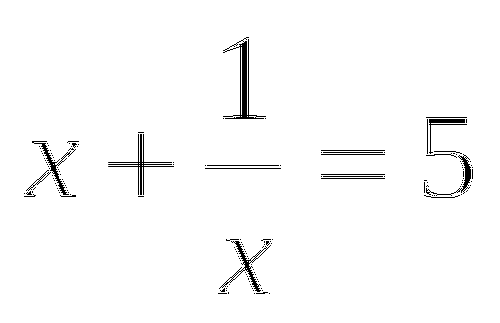, найти .

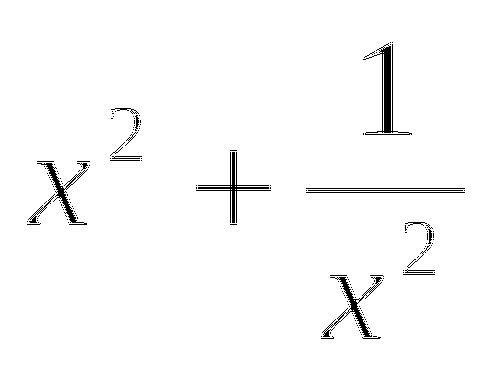(5 баллов)

5. При каких значениях параметра a уравнение 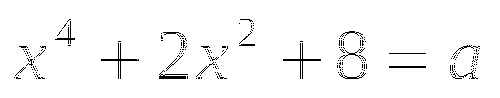не имеет корней?

(5 баллов)

Ответы и указания

к заданиям районного этапа олимпиады

школьников по математике

2013-2014 учебный год

11 класс

1. Указание. Использовать неравенство ;

1) ; 2) ; 3) . Складывая три неравенства, получим то, что нужно было доказать.

2. Пусть , тогда уравнение принимает вид .

Найдём нули модулей Решим уравнение:

1) Вернёмся к замене ; корней нет.

2)

3) Вернёмся к замене ; два корня. .

Ответ: .

3. Указание.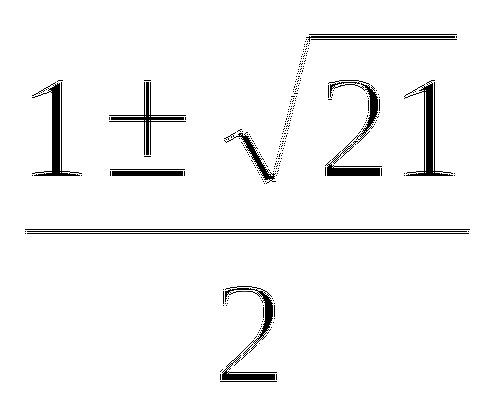

Сделать рисунок и рассмотреть три пары подобных треугольников, записать пропорциональность сторон, обозначив высоту искомой трапеции за h, а построенной трапеции за .

Пусть ДМNЕ искомая трапеция, точка С точка пересечения продолжения диагоналей, а АВ искомый отрезок. Тогда треугольники ДМЕ и СМА; ДNЕ и ВNС; МNЕ и АСЕ являются подобными, поэтому

Откуда следует АС=СВ, а из первого и третьего равенства следует АС=.

Ответ: .

4. Возвести в квадрат обе части уравнения ,

Ответ: .

5. Уравнение не имеет корней, если . ; .

Ответ:

Задания районного этапа олимпиады

школьников по математике

2013-2014 учебный год

9 класс

1. Известно, что 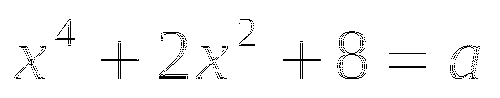, 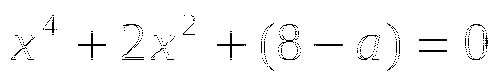. Чему может равняться .

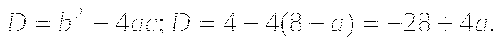(5 баллов)

2. Решите уравнение: .

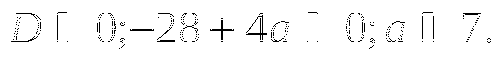(5 баллов)

3. На сторонах АВ и ВС параллелограмма АВСД вне его построены равносторонние треугольники АВМ и ВСN. Докажите, что треугольник ДМN равносторонний.

(5 баллов)

4. Четверо ребят - Алексей, Борис, Владимир и Григорий участвовали в лыжных гонках. На следующий день, на вопрос кто какое место занял, они ответили так:

Алексей: Я не был ни первым и ни последним;

Борис: Я не был последним;

Владимир: Я был первым;

Григорий: Я был последним.

Известно, что три из этих ответов были правдивыми, а один - ложью. Кто сказал правду? Кто был первым?

(5 баллов)

5. Среди 81 монеты имеется одна фальшивая (более лёгкая) монета. Как её найти, используя не более четырёх взвешиваний.

(5 баллов)

Ответы и указания

к заданиям районного этапа олимпиады

школьников по математике

2013-2014 учебный год

9 класс

1. Указание. Возведите обе части выражения в квадрат.

Ответ. 15.

2. Умножьте обе части уравнения на 2, , , после группировки получим , откуда .

Ответ: .

3. Построить. Стороны треугольника ДМN найти по теореме косинусов. Эти стороны равны.

4. Проверить каждое рассуждение, предположив, что оно ложно. Если солгал Алексей, то солгали ещё Владимир и Григорий, чего не может быть : Пусть солгал Борис, тогда он был последним, но Григорий: также утверждает, что он был последним. Значит, данного случая тоже не может быть. Пусть солгал Владимир, тогда он был ни первым, в этом случае всё получается и первым был Борис. Последний случай, когда солгал Григорий не может быть, так как тогда последним никто из ребят не был.

Ответ. Правду сказали Алексей, Борис и Григорий. Первым был Борис.

5. Разделим монеты на три кучки по 27 монет. Взвесим первую и вторую кучки. Если весы в равновесии, то фальшивая монета в третьей кучке.

Если весы не в равновесии, то фальшивая монета в той кучке, которая легче. После этого разбиваем кучку из 27 монет (в которой есть фальшивая монета) на три кучки по 9 монет и вторым взвешиванием определяем более лёгкую кучку. Третьим взвешиванием определяем более лёгкую тройку монет. И, наконец, четвёртым взвешиванием определяем фальшивую монету.

Задания районного этапа олимпиады

школьников по математике

2013-2014 учебный год

10 класс

1. Упростите выражение: и найти его значение, если .

(6 баллов)

2. Решите уравнение .

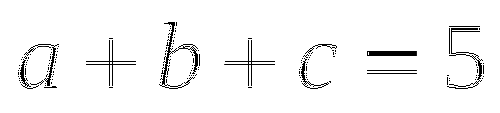(5 баллов)

3. Из горячего крана ванна заполняется за 23 минуты, из холодного за 17 минут. Маша открыла сначала горячий кран. Через сколько минут она должна открыть холодный кран, чтобы к моменту наполнения ванны горячей воды налилось в 1,5 раза больше, чем холодной?

(8 баллов)

4. Найдите площадь прямоугольного треугольника, если радиус описанной около него окружности равен 5, а радиус вписанной в него окружности равен 2.

(5 баллов)

5. Сколько цифр содержит число ?

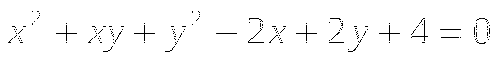(5 баллов)

Ответы и указания

к заданиям районного этапа олимпиады

школьников по математике

2013-2014 учебный год

10 класс.

1. Складываем последние два слагаемых, затем полученную сумму с впереди стоящим слагаемым и т. д. В результате получим . Подставляя вместо , получаем ответ .

2. Рассмотреть два случая, когда и решить квадратные уравнения.

Ответ: -5; 3.

3. За 1минуту наливается горячей водой часть ванны, а за 1минуту наливается холодной водой часть ванны. Пусть холодной воды налили х литров, а горячей 1,5х литров. Итак, , откуда , то есть холодной водой заполнено ванны, горячей ванны. Для заполнения холодной водой ванны потребуется минут, а горячей минут, значит кран нужно открыть через 7 минут.

4. Используя свойства вписанной и описанной окружности и теорему Пифагора, запишем систему. . Откуда . Площадь равна .

Ответ: .

5. .

Ответ: 13 цифр.