Конспект урока по темеГрафическое решение уравнений сводящихся к линейному уравнению

Графическое решение уравнений сводящихся к линейному уравнению

Предварительная подготовка к уроку: учащиеся должны знать следующие темы: «Линейное уравнение», «Линейная функция и её график», «Взаимное расположение графиков линейных функций», владеть навыками построения графиков линейных функций.

Цели урока:

• развить навыки графического решения уравнений, сводящихся к линейным;

• выработка у учащихся умения обобщать изученный материал, анализировать, сопоставлять и делать выводы;

• развивать навыки использования компьютера и мультимедийных учебных программ для выполнения лабораторно-практических работ по алгебре.

Оборудование: оборудование кабинета информатики (ПК, проектор, экран), программное обеспечение (МК-плеер 6.1, Математика. Коллекция интерактивных моделей. 5-11 классы).

Тип урока: лабораторно-практический.

Ход урока

1. Актуализация знаний (устная работа)

• Что такое уравнение? (Равенство содержащие неизвестное (переменную)).

• Что такое корень уравнения? (Значение переменной (число), при котором уравнение обращается в верное равенство.)

• Что значит решить уравнение? (Найти все его корни, или доказать, что корней нет.)

• Дайте определение линейной функции. (Линейной функцией называется функция, которую можно задать формулой вида у=ax+b, где х - независимая переменная, a, b - некоторые числа.)

• Что является графиком линейной функции? (Прямая.)

• Какой формулой задается график линейной функции? (у=ax+b).

• Что обозначает х в данной формуле (Это независимая переменная.)

• Что такое а и b? (Некоторые числа, причем а - угловой коэффициент.)

• Что из себя представляет график функции y=b? (Прямую параллельную оси абсцисс, a=0 - угловой коэффициент равен нулю.)

• Что из себя представляет график функции y=0? (Ось абсцисс, a=0 - угловой коэффициент равен нулю, b=0 - сдвига вдоль оси ординат нет.)

2. Выполнение заданий (фронтальная работа с классом)

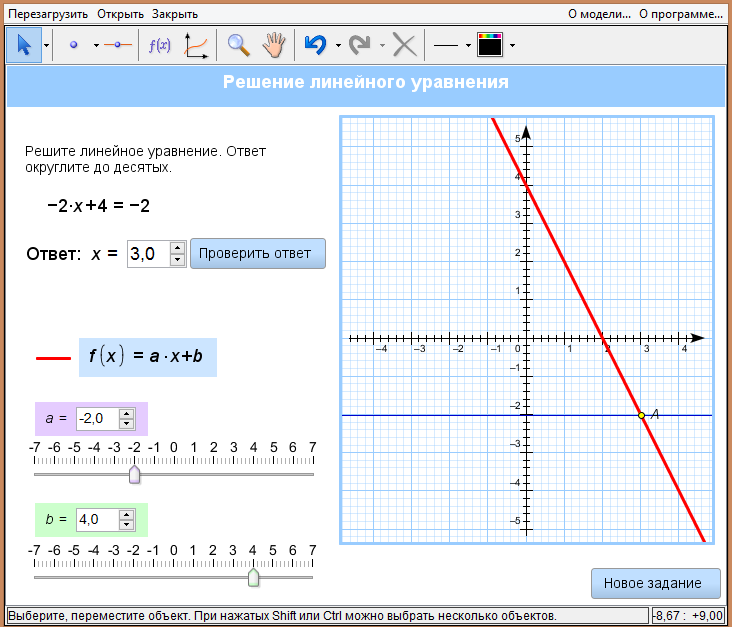
1. Используя модель, построить графическое решение для трех случайно сгенерированных линейных уравнений, используя для построения левой части уравнения значения параметров а и b, для правой части горизонтальную прямую.

Например:

2. Используя построение графиков функций , рассмотреть решения следующих линейных уравнений:

1. 2(3х-1)=4(х+3)

2. 2(3х-1)=4(х+3)-14+2х

3. 2(3х-1)=4(х+3)+2х

Для этого (рассмотрим на примере уравнения 2(3х-1)=4(х+3)):

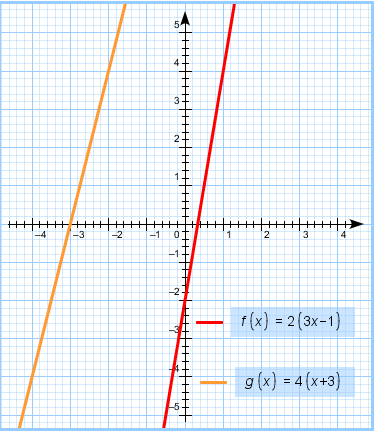
1. Построить график для левой части уравнения f(x)= 2(3х-1)

2. Построить график для правой части уравнения g(x)= 4(х+3)

</

3. Используя строку статуса определить координаты курсора, наведенного на точку пересечения соответствующих прямых, значение абсциссы - приближенное решение данного уравнения.

3. Аналитическим способом решить уравнение:

2(3х-1)=4(х+3)

6х-2=4х+12

6х-4х=12+2

2х=14

х=7.

4. Аналогично найти решения для второго и третьего уравнений (графическим и аналитическим способами).

5. Заполнить таблицу:

(значение абсциссы)

Решение уравнения

(аналитическим способом)

Выводы

1. 2(3х-1)=4(х+3)

прямые пересекаются в точке, х7,01

х=7

а≠0, b≠0

один корень

2. 2(3х-1)=4(х+3)-14+2х

прямые совпали

0х=0

a=0, b=0

х - любое число, много корней

3. 2(3х-1)=4(х+3)+2х

прямые параллельны

0х=14

a=0 , b≠0

нет решений

3. Лабораторно-практическая часть урока (работа за компьютерами в парах)

1. Решить уравнения графическим способом (найти приближенные решения уравнений).

2. Решить уравнения аналитическим способом (найти точные решения уравнений).

3. Сделать выводы.

4. Результаты работы оформить в виде таблицы:

(значение абсциссы)

Решение уравнения

(аналитическим способом)

Выводы

1. 7х-5=3х+7

2. 3(3х+4)=2(4х+5)+х

3. 6(2х+3)-8х=4х+18

4. 12-(4х-18)=(36+4х)+(18-6х)

5. 1,6х-(х-2,8)=(0,2х+1,5)-0,7

6. 0,25х-31=х-18+5

7. (1,5х-37)-(1,5х-73)=36