рабочая программа по алгебре 7 класс Макарычев

Пояснительная записка

к рабочей программе алгебра 7 класс

Рабочая программа учебного курса алгебры для 7 класса составлена в соответствии с федеральным компонентом государственного образовательного стандарта основного общего образования по математике, на основе авторской программы для общеобразовательных учреждений Макарычев Ю.Н. .Алгебра.7-9 классы //Сборник программ по алгебре 7-9 классы. М.Просвещение,2009 составитель Т.А. Бурмистрова.

Данная рабочая программа составлена для изучения алгебры по учебнику Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б., под редакцией Теляковского С.А. «Алгебра 7 класс» (издательство «Просвещение» 2010 год).

Программа рассчитана на 105 часов

10 часов отведено для проведения текущих контрольных работ.

В результате изучения курса алгебры 7 класса обучающиеся должны:

знать/понимать

• существо понятия математического доказательства; примеры доказательств;

• существо понятия алгоритма; примеры алгоритмов;

• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• примеры статистических закономерностей и выводов;

• каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики.

Алгебра

уметь

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

• выполнять основные действия со степенями с натуральными показателями, с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

• решать линейные уравнения решать линейные решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• изображать числа точками на координатной прямой;

• определять координаты точки плоскости, строить точки с заданными координатами;

• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• применять графические представления при решении уравнений, систем, неравенств;

• описывать свойства изученных функций (у=кх, где к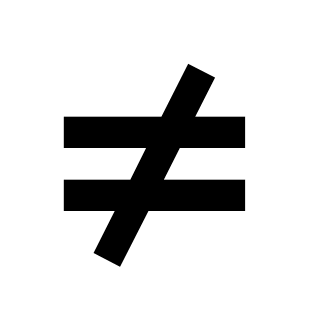0, у=кх+b, у=х², у=х³), строить их графики.

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;

• описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

• интерпретации графиков реальных зависимостей между величинами.

Элементы логики, комбинаторики,
статистики и теории вероятностей

уметь

• проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;

• решать комбинаторные задачи путем систематического перебора возможных вариантов, вычислять средние значения результатов измерений;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выстраивания аргументации при доказательстве (в форме монолога и диалога);

• распознавания логически некорректных рассуждений;

• записи математических утверждений, доказательств;

• анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;

• решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;

• решения учебных и практических задач, требующих систематического перебора вариантов;

• понимания статистических утверждений.

Содержание обучения

1. Выражения, тождества, уравнения (19 часов)

Числовые выражения с переменными. Простейшие преобразования выражений. Уравнение, корень уравнения. Линейное уравнение с одной переменной. Решение текстовых задач методом составления уравнений. Статистические характеристики.

Основная цель - систематизировать и обобщить сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной.

Первая тема курса 7 класса является связующим звеном между курсом математики 5-6 классов и курсом алгебры. В ней закрепляются вычислительные навыки, систематизируются и обобщаются сведения о преобразованиях выражений и решении уравнений.

Нахождение значений числовых и буквенных выражений даёт возможность повторить с обучающимися правила действий с рациональными числами. Умения выполнять арифметические действия с рациональными числами являются опорными для всего курса алгебры. Следует выяснить, насколько прочно овладели ими учащиеся, и в случае необходимости организовать повторение с целью ликвидации выявленных пробелов. Развитию навыков вычислений должно уделяться серьезное внимание и в дальнейшем при изучении других тем курса алгебры.

В связи с рассмотрением вопроса о сравнении значений выражений расширяются сведения о неравенствах: вводятся знаки ≥ и ≤, дается понятие о двойных неравенствах.

При рассмотрении преобразований выражений формально-оперативные умения остаются на том же уровне, учащиеся поднимаются на новую ступень в овладении теорией. Вводятся понятия «тождественно равные выражения», «тождество», «тождественное преобразование выражений», содержание которых будет постоянно раскрываться и углубляться при изучении преобразований различных алгебраических выражений. Подчеркивается, что основу тождественных преобразований составляют свойства действий над числами.

Усиливается роль теоретических сведений при рассмотрении уравнений. С целью обеспечения осознанного восприятия обучающимися алгоритмов решения уравнений вводится вспомогательное понятие равносильности уравнений, формулируются и разъясняются на конкретных примерах свойства равносильности. Дается понятие линейного уравнения и исследуется вопрос о числе его корней. В системе упражнений особое внимание уделяется решению уравнений вида ах=b при различных значениях а и b. Продолжается работа по формированию у обучающихся умения использовать аппарат уравнений как средство для решения текстовых задач. Уровень сложности задач здесь остается таким же, как в 6 классе.

Изучение темы завершается ознакомлением обучающихся с простейшими статистическими характеристиками: средним арифметическим, модой, медианой, размахом. Учащиеся должны уметь пользовать эти характеристики для анализа ряда данных в несложных ситуациях.

2. Функции (12 часов)

Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и её график.

Основная цель - ознакомить обучающихся с важнейшими функциональными понятиями и с графиками прямой пропорциональности и линейной функции общего вида.

Данная тема является начальным этапом в систематической функциональной подготовке обучающихся. Здесь вводятся такие понятия, как функция, аргумент, область определения функции, график функции. Функция трактуется как зависимость одной переменной от другой. Учащиеся получают первое представление о способах задания функции. В данной теме начинается работа по формированию у обучающихся умений находить по формуле значение функции по известному значению аргумента, выполнять ту же задачу по графику и решать по графику обратную задачу.

Функциональные понятия получают свою конкретизацию при изучении линейной функции и ее частного вида - прямой пропорциональности. Умения строить и читать графики этих функций широко используются как в самом курсе алгебры, так и в курсах геометрии и физики. Учащиеся должны понимать, как влияет знак коэффициента на расположение в координатной плоскости графика функции у=кх, где к0, как зависит от значений к и b взаимное расположение графиков двух функций вида у=кх+b.

Формирование всех функциональных понятий и выработка соответствующих навыков, а также изучение конкретных функций сопровождаются рассмотрением примеров реальных зависимостей между величинами, что способствует усилению прикладной направленности курса алгебры.

3. Степень с натуральным показателем (13 часов)

Степень с натуральным показателем и ее свойства. Одночлен. Функции у=х², у=х³ и их графики.

Основная цель - выработать умение выполнять действия над степенями с натуральными показателями.

В данной теме дается определение степени с натуральным показателем. В курсе математики 6 класса учащиеся уже встречались с примерами возведения чисел в степень. В связи с вычислением значений степени в 7 классе дается представление о нахождении значений степени с помощью калькулятора; Рассматриваются свойства степени с натуральным показателем: На примере доказательства свойств а^m · аⁿ = а^m+n; а^m : аⁿ = а^m-n, где m > n; (а^m)ⁿ = а^m·n; (ab)^m = a^mb^m учащиеся впервые знакомятся с доказательствами, проводимыми на алгебраическом материале. Указанные свойства степени с натуральным показателем находят применение при умножении одночленов и возведении одночленов в степень. При нахождении значений выражений содержащих степени, особое внимание следует обратить на порядок действий.

Рассмотрение функций у=х², у=х³ позволяет продолжить работу по формированию умений строить и читать графики функций. Важно обратить внимание обучающихся на особенности графика функции у=х²:график проходит через начало координат, ось Оу является его осью симметрии, график расположен в верхней полуплоскости.

Умение строить графики функций у=х² и у=х³ используется для ознакомления обучающихся с графическим способом решения уравнений.

4. Многочлены (18 часов)

Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочленов на множители.

Основная цель - выработать умение выполнять сложе­ние, вычитание, умножение многочленов и разложение многочленов на множители.

Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений. Формируемые здесь формально-оперативные умения являются опорными при изучении действий с рациональными дробями, корнями, степенями с рациональными показателями.

Изучение темы начинается с введения понятий многочлена, стандартного вида многочлена, степени многочлена. Основное место в этой теме занимают алгоритмы действий с многочленами - сложение, вычитание и умножение. Учащиеся должны понимать, что сумму, разность, произведение многочленов всегда можно представить в виде многочлена. Действия сложения, вычитания и умножения многочленов выступают как составной компонент в заданиях на преобразования целых выражений. Поэтому нецелесообразно переходить к комбинированным заданиям прежде, чем усвоены основные алгоритмы.

Серьезное внимание в этой теме уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Соответствующие преобразования находят широкое применение как в курсе 7 класса, так и в последующих курсах, особенно в действиях с рациональными дробями.

В данной теме учащиеся встречаются с примерами использования рассматриваемых преобразований при решении разнообразных задач, в частности при решении уравнений. Это позволяет в ходе изучения темы продолжить работу по формированию умения решать уравнения, а также решать задачи методом составления уравнений. В число упражнений включаются несложные задания на доказательство тождества.

5. Формулы сокращенного умножения (18 часов)

Формулы (а - b )(а + b ) = а² - b ², (а ± b)² = а²± 2а b + b², (а ± b)³ = а³ ± За²b + За b² ± b³, (а ± b) (а² а b + b²) = а³ ± b³. Применение формул сокращённого умножения в преобразованиях выражений.

Основная цель - выработать умение применять формулы сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители.

В данной теме продолжается работа по формированию у обучающихся умения выполнять тождественные преобразования целых выражений. Основное внимание в теме уделяется формулам (а - b)(а + b) = а² - b ², (а ± b)² = а²± 2а b + b². Учащиеся должны знать эти формулы и соответствующие словесные формулировки, уметь применять их как «слева направо», так и «справа налево».

Наряду с указанными рассматриваются также формулы (а ± b)³ = а³ ± За²b + За b² ± b³, (а ± b) (а² а b + b²) = а³ ± b³. Однако они находят меньшее применение в курсе, поэтому не следует излишне увлекаться выполнением упражнений на их использование.

В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для решения широкого круга задач.

6. Системы линейных уравнений (15 часов)

Система уравнений. Решение системы двух линейных уравнений с двумя переменными и его геометрическая интерпретация. Решение текстовых задач методом составления систем уравнений.

Основная цель - ознакомить обучающихся со способом решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и применять их при решении текстовых задач.

Изучение систем уравнений распределяется между курсами 7 и 9 классов. В 7 классе вводится понятие системы и рассматриваются системы линейных уравнений.

Изложение начинается с введения понятия «линейное уравнение с двумя переменными». В систему упражнений включаются несложные задания на решение линейных уравнений с двумя переменными в целых числах.

Формируется умение строить график уравнения ах + bу=с, где а≠0 или b≠0, при различных значениях а, b, с. Введение графических образов даёт возможность наглядно исследовать вопрос о числе решений системы двух линейных уравнений с двумя переменными.

Основное место в данной теме занимает изучение алгоритмов решения систем двух линейных уравнений с двумя переменными способом подстановки и способом сложения. Введение систем позволяет значительно расширить круг текстовых задач, решаемых с помощью аппарата алгебры. Применение систем упрощает процесс перевода данных задачи с обычного языка на язык уравнений.

7. Повторение (10 часов)

Основная цель - повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры 7 класса.

Итоговый зачет, итоговая контрольная работа.

Календарно-тематическое планирование учебного материала

по алгебре 7 класс

№ п/п

Содержание материала

Кол - во

часов

Даты проведения

план

факт

Выражения и их преобразования. Уравнения.19ч.

Числовые выражения.

1

Выражения с переменными.

1

Сравнение значение выражений.

1

Свойства действий над числами.

1

Тождества.

1

Тождественные преобразования выражений

1

Правила раскрытия скобок.

1

Контрольная работа №1 по теме «Выражения и их преобразования».

1ч.

Уравнение и его корни.

1

Линейное уравнение с одной переменной.

1

Алгоритм решения линейного уравнения с одной переменной.

1

Решение задач с помощью уравнений.

1

Выбор, обозначение неизвестного и составление уравнения по условию задачи.

1

Исследование результата уравнения в соответствии с условием задачи.

1

Статистические характеристики. Сбор и группировка статистических данных;

1

Среднее арифметическое, размах и мода.

1

Наглядное представление статистической информации.

1

Медиана, как статистическая характеристика.

1

Контрольная работа №2 по теме «Уравнение».

1ч.

Функции. 12ч.

20.

Что такое функция.

1

21.

Вычисление значений функции по формуле.

1

22.

График функции.

1

23.

Чтение графика. Построение по точкам графика функции, заданной формулой.

1

24.

Прямая пропорциональность.

1

25.

Работа с графиком прямой пропорциональности.

1

26.

Линейная функция и ее график.

1

27.

Построение и чтение графика функции у = kх + b, при различных значениях к и b.

1

28.

Нахождение координат точек пересечения с осями координат графика функции у = kх + b.

1

29.

Взаимное расположение графиков линейных функций.

1

30.

Геометрический смысл коэффициентов к и b.

1

31.

Контрольная работа №3 по теме «Функции».

1ч.

Степень с натуральным показателем. 13ч.

32.

Определение степени с натуральным показателем.

1

33.

Свойства степеней с натуральным показателем.

1

34.

Умножение и деление степеней.

1

35.

Применение свойства степени.

1

36.

Возведение в степень произведения .

1

37.

Возведение в степень степени.

38.

Выполнение действий со степенями.

39.

Одночлен и его стандартный вид.

1

40.

Умножение одночленов. Возведение в степень.

1

41.

Функции у = х² , у = х³ и их графики.

1

42.

Графическое решение уравнений.

1

43.

Абсолютная и относительная погрешности погрешность и точность приближения.

1

44.

Контрольная работа №4 по теме «Степень с натуральным показателем».

1ч.

Многочлены. 18ч.

45.

Многочлен и его стандартный вид.

1

46.

Сложение и вычитание многочленов.

1

47.

Алгоритм сложения и вычитания многочленов.

1

48.

Применение правил сложения и вычитания.

1

49.

Умножение одночлена на многочлен.

1

50.

Преобразование произведения одночлена и многочлена в многочлен стандартного вида.

1

51.

Приведение подобных слагаемых многочлена.

1

52.

Вынесение общего множителя за скобки.

1

53.

Разложение многочлена на множители.

1

54.

Контрольная работа №5 по теме «Сложение и вычитание многочленов».

1ч.

55.

Умножение многочлена на многочлен.

1

56.

Преобразование произведения двух многочленов в многочлен стандартного вида.

1

57.

Разложение многочлена на множители способом группировки.

1

58.

Применение способа группировки при упрощении выражений.

1

59.

Решение уравнений путем разложения на множители.

1

60.

Доказательство тождеств.

1

61.

Тождественные преобразования выражений.

1

62.

Контрольная работа №6 по теме «Умножение и деление многочленов».

1ч.

Формулы сокращенного умножения. 18ч.

63.

Возведение в квадрат суммы и разности двух выражений.

1

64.

Преобразование целых выражений с помощью формул (а  b)² = a²  2ab + b².

1

65.

Разложение на множители с помощью формул квадрата суммы и квадрата разности.

1

66.

Преобразование многочлена с помощью формул a²  2ab + b² = (а  b)².

1

67.

Умножение разности двух выражений на их сумму.

1

68.

Применение формулы (а - b)(a + b) = a²-b².

1

69.

Разложение разности квадратов на множители.

1

70.

Применение формулы a²-b²= (а - b)(a + b) для разложения на множители.

1

71.

Преобразование многочлена с помощью формулы a²-b²= (а - b)(a + b).

1

72.

Контрольная работа № 7 по теме «Формулы сокращенного умножения».

1ч.

73.

Разложение на множители суммы и разности кубов.

1ч.

74.

Преобразование целого выражения в многочлен.

1

75.

Преобразование произведения двух или нескольких многочленов в многочлен стандартного вида.

1

76.

Применение различных способов для разложения на множители.

1

77.

Нахождение значение многочлена при заданных значениях переменной.

1

78.

Применение преобразований целых выражений.

1

79.

Упрощение выражений. Подготовка к контрольной работе.

1

80.

Контрольная работа № 8 по теме «Преобразование выражений»

1ч.

Системы линейных уравнений. 15ч.

81.

Линейное уравнение с двумя переменными.

1

82.

График линейного уравнения с двумя переменными. Построение графика функции ax + by + c = 0.

1

83.

Системы линейных уравнений с двумя переменными.

1

84.

Графический метод решения систем уравнений.

1

85.

Взаимное расположение двух прямых при различных решениях системы уравнений

1

86.

Способ подстановки.

1

87.

Решение систем уравнений способом подстановки.

1

88.

Способ сложения.

1

89.

Способ сложения решения систем уравнений.

1

90.

Алгоритм решения систем уравнений с двумя переменными способом сложения.

1

91.

Решение задач с помощью систем уравнений.

1

92.

Составление систем уравнений в типовых задачах.

1

93.

Исследование полученных ответов по условию задачи.

1

94.

Применение систем линейных уравнений при решении задач. Подготовка к контрольной работе.

1

95.

Контрольная работа № 9 по теме «Системы линейных уравнений».

1ч.

Повторение. Решение задач. 10 ч.

96.

Выражения и их преобразования. Уравнения.

1

97.

Степень с натуральным показателем.

1

98-99

Итоговая контрольная работа.

2

100.

Анализ итоговой контрольной работы.

1

101.

Формулы сокращенного умножения.

1

101

Системы линейных уравнений.

1

102.

Решение задач с помощью уравнений, систем уравнений.

1

103.

Графики функций.

1

104.

Итоговое тестирование по курсу алгебры 7 класса.

1

105.

Итоговый урок.

1

КОНТРОЛЬНЫЕ РАБОТЫ

КОНТРОЛЬНАЯ РАБОТА № I

КОНТРОЛЬНАЯ РАБОТА № 2

КОНТРОЛЬНАЯ РАБОТА № 3

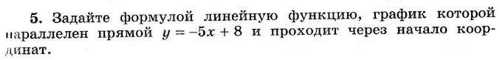
КОНТРОЛЬНАЯ РАБОТА № 4

КОНТРОЛЬНАЯ РАБОТА № 5

КОНТРОЛЬНАЯ РАБОТА № 6

КОНТРОЛЬНАЯ РАБОТА № 7

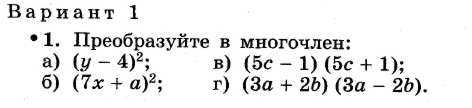
КОНТРОЛЬНАЯ РАБОТА № 8

КОНТРОЛЬНАЯ РАБОТА № 9

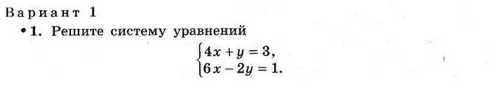
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА

ИТОГОВЫЙ ТЕСТ ЗА КУРС 7 КЛАССА

Список литературы

1. Алгебра-7:учебник/автор: Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова, Просвещение, 2012 г.

2. Примерная программа общеобразовательных учреждений по алгебре 7-9 классы, к учебному комплексу для 7-9 классов (авторы Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова Ю.Н., составитель Т.А. Бурмистрова - М: «Просвещение», 2009. - с. 22-26).

3. Дидактические материалы по алгебре 7 класс. Авторы: Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова, Просвещение, 2009 г.

4. Тесты «Алгебра 7-9» под редакцией Алтынова П.И.