Универсальная формула. Исследовательский проект по математике.

Бюджетное общеобразовательное учреждение города Омска

«Средняя общеобразовательная школа № 152»

Универсальная формула

Исследовательский проект по математике

Свинцицкая Дарья,



ученица 8 класса,

БОУ г. Омска «СОШ №152»



Руководитель:



Никитина Людмила Ивановна,



учитель физики и математики,

БОУ г. Омска «СОШ №152»

ОМСК, 2015

ОГЛАВЛЕНИЕ

Введение:

Актуальность темы.

Цели и задачи темы.

Методы исследования.

Наглядность.

Практическая значимость проекта.

… стр. 3



Глава 1. Теоретическая часть

1. Понятие объема, единицы измерения объема.

2. Свойства объемов тел.

1.3 Формулы для вычисления объемов геометрических тел.

1.4 Формула Симпсона. …стр. 5

Глава 2. Практическая часть

2.1 Нахождение объёмов правильных геометрических тел.

2.2 Практическое применение универсальной формулы.

... стр. 9

Заключение … стр. 19

Библиографический список …стр. 20

Актуальность исследования:

Одна из интереснейших задач геометрии, результат решения которой важен и в физике, и в химии, и в других областях - определение объемов. Мир вокруг кажется настолько простым и понятным, что определенные школьные знания относят к разряду «ненужных». Но стоит столкнуться, к примеру, с транспортировкой и возникает вопрос о том, как посчитать объем груза. Вопрос определения объемов играет немаловажную роль в строительстве. Возведение домов, других сооружений - дело затратное, стройматериалы требуют внимательного отношения и предельно точного расчета. Некоторые прикладные задачи требуют знаний об объеме зданий и сооружений. Современные квартиры и офисы невозможно представить без системы отопления. Как посчитать объем системы отопления?

Что предпринимать, если форма тела не столь четко определена? Определение объема сложных геометрических конструкций - работа не из легких. Существует ли такая универсальная формула для нахождения объёма тел сложной формы?

Цель работы: Найти универсальную формулу для вычисления объемов нестандартных тел и показать применение этой формулы в различных областях науки, сельском хозяйстве, производстве, а так же в различных жизненных ситуациях.

Задачи:

1. Изучить понятие объема, единицы измерения объема, свойства объемов тел.

2. Познакомиться с формулами для вычисления объемов геометрических тел: куба, прямоугольного параллелепипеда, пирамиды, конуса, цилиндра, шара.

3. Познакомиться с формулой Симпсона.

4. Доказать, что объем геометрического тела можно найти при помощи формулы Симпсона.

5. Собрать и обработать информацию о применении формулы Симпсона в различных жизненных ситуациях.

Методы исследования

Теоретические методы:

Моделирование - практические действия с «заместителем» объекта - моделью.

Анализ и синтез. Методами анализа и синтеза проводится, в частности, начальный этап исследования - изучение специальной литературы по теории вопроса.

Эмпирические методы:

Сравнение - установить сходство предметов и явлений.

Наглядность: модели геометрических тел, таблицы.



Тип проекта: информационно-исследовательский.

Практическая значимость работы:

Тема данного проекта актуальна не только для учащихся, но и для взрослых. Умение вычислять объемы различных тел и особенно тел сложной конструкции может пригодиться в любой сфере жизнедеятельности человека.

Глава 1.

1.1 Понятие объема, единицы измерения объема

Наш мир трехгранен, это значит, что у всех тел в природе есть три характеристики: длина, ширина и высота. В совокупности эти величины объединяются в физической величине, называемой объемом тел. Объем - это вместимость геометрического тела, т. е. части пространства, ограниченной одной или несколькими замкнутыми поверхностями. В Международной системе единиц СИ объем измеряется в м³ . [1]

1.2 Свойства объемов тел

Любое тело можно разбить на более простые части. Объем равен сумме объемов его отдельных частей. Равновеликие тела имеют равные объемы. Единицей объема считают объем куба с ребром единичной длины. [1]

1.3 Формулы для вычисления объемов геометрических тел

Все эти формулы объединяет один математический принцип: произведение высоты фигуры на площадь ее основания (V=S*h, где V- объем, S- площадь основания, h - высота фигуры). Вследствие того, что основания у таких фигур представляют собой различные плоские фигуры: квадрат, ромб, треугольник, круг и т.д., тогда и общая формула объема видоизменяется, из-за разных формул площадей основания.

Объем куба

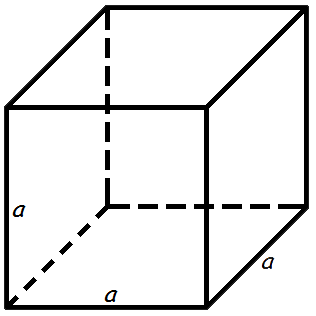
Объем куба равен кубу длины его грани.

Формула объема куба: V = a³

V - объем куба, a - длина грани куба.

Объем прямоугольного параллелепипеда

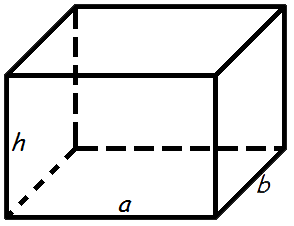
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

Формула объема прямоугольного параллелепипеда: V = a · b · h

V - объем прямоугольного параллелепипеда, a - длина, b - ширина, h - высота.

Объем пирамиды

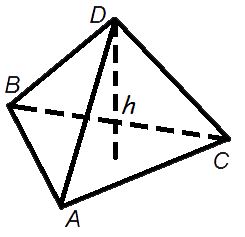
Объем пирамиды равен трети от произведения площади ее основания на высоту.Формула объема пирамиды: V =

1

S_o · h

3

V - объем пирамиды, S_o - площадь основания пирамиды, h - длина высоты пирамиды.

Объем цилиндра

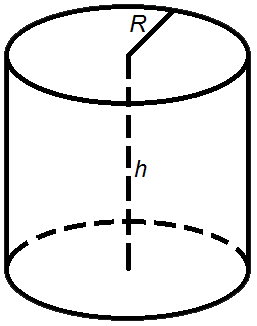
Объем цилиндра равен произведению площади его основания на высоту.

Формулы объема цилиндра: V = π R² h, V = S_o h

V - объем цилиндра, S_o - площадь основания цилиндра, R - радиус цилиндра, h - высота цилиндра, π = 3,14.

Объем конуса

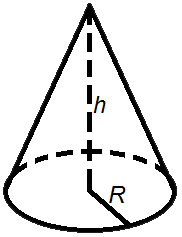
Объем конуса равен трети от произведению площади его основания на высоту.Формула объема конуса: V =

1

πR² h

3

V - объем конуса, S_o - площадь основания конуса, R - радиус основания конуса, h - высота конуса, π = 3,14.

Объем шара

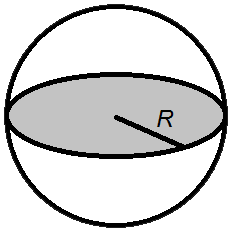
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.Формула объема шара: V =

4

π R³

3

V - объем шара, R - радиус шара, π = 3,14. [1]

1.4 Формула Симпсона

То́мас Си́мпсон (20 августа 1710 -14 мая 1761) - английский математик. В 1746 году Симпсон избран в члены Лондонского королевского общества, а ранее - в члены основанного в 1717 году в Лондоне Математического общества. В 1758 избран иностранным членом Шведской королевской академии наук. Назначенный профессором в Королевскую военную академию в Вулидже, Симпсон составил учебники по элементарной математике. В особых отделах геометрии рассматриваются задачи о наибольших и наименьших величинах, решаемые с помощью элементарной геометрии, правильные многогранники, измерение поверхностей, объёмы тел и, наконец, смешанные задачи.

Вот эта замечательная формула, известная в математике под названием формулы Симпсона:

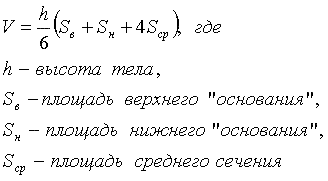[4]

Глава 2

2.1 Нахождение объёмов правильных геометрических тел

Цель исследования: Доказать, что формула Симпсона действительно справедлива для разного рода геометрических фигур.

Задачи исследования:

1. Используя модели геометрических фигур, рассмотреть способы нахождения объемов при помощи обычных формул и формулы Симпсона.

2. Сравнить два решения одной задачи.

3. Проанализировать рациональность применения универсальной формулы на конкретных моделях.

Задача № 1.

Вычисляем объём модели куба по обычной формуле. Для этого измеряем ребро модели куба: а = 12,5 см. V=a³ = 1953,125 cм³

Вычисляем объем модели куба по формуле Симпсона V = h/6(S_{нижнего основания} + S_{верхнего основания} + 4S_{среднего сечения}): площади верхнего, нижнего основания и среднего сечения равны между собой 12,5 * 12,5 = 156,25 см², h= а.

V = 12,5/6( 156,25 +156,25 + 4* 156,25) = (12,5/6)* (6*156,25) = 12,5*156,25 =1953,125 см³

Задача № 2.

Вычисляем объём модели правильной шестиугольной пирамиды по обычной формуле. Для этого измеряем высоту модели h = 17,2 см и сторону основания а = 6,5 см. Вычисляем S _{основания}= ½(Р_{основания}* r) = 1/2(6*6,5*5,6) = 109,2 см² , r = Rcos(180/n) = 6,5 *cos(180\6) = 5,6 см, R = а = 6,5 см, V =1/3(S*h) = 1/3(109,2*17,2) = 626 cм³

Вычисляем объем модели по формуле Симпсона V = h/6(S_{нижнего основания} + S_{верхнего основания} + 4S_{среднего сечения}): площадь нижнего основания = 109,2 см² , площадь верхнего основания = 0 и площадь среднего сечения =27,72 см² S _{сечения}= ½(Р_{сечения}* r) = 1/2(6*3,3*2,8) = 27,72 см² , r = Rcos(180/n) = 3,3 *cos(180\6) = 2,8 см, R = а = 6,5/2 = 3,3 см, h= 17,2 см.

V = 17,2/6( 0 +109,2 + 4* 27,72) = 626 см³

Задача № 3.

Вычисляем объём модели цилиндра по обычной формуле. Для этого измеряем высоту модели h = 20,4 см и радиус основания R = 14 см. Вычисляем S = π *R² = 3,14* 14² см² , V =S*h = 3,14*196*20,4 = 12554,976 cм³

Вычисляем объем модели по формуле Симпсона V = h/6(Sнижнего основания + Sверхнего основания + 4Sсреднего сечения): площади верхнего, нижнего основания и среднего сечения равны между собой S = π *R² = 3,14* 14² = 615,44см², h= 20,4 см.

V = 20,4/6( 615,44 +615,44 + 4* 615,44) = 20,4/6*(6*615,44) = 20,4*615,44 = 12554,976 см³

Задача № 4.

Вычисляем объём модели конуса по обычной формуле. Для этого измеряем высоту модели h = 21 см и радиус основания R = 6 см. Вычисляем S = π *R² = 3,14* 6² см² , V =1/3(S*h) = 1/3(3,14*36*21) = 791,28 cм³

Вычисляем объем модели по формуле Симпсона V = h/6(Sнижнего основания + Sверхнего основания + 4Sсреднего сечения): площадь нижнего основания = 3,14* 6² = 113,04 см², площадь верхнего основания = 0 и площадь среднего сечения S = π *(R/2)² = 3,14* 3² = 28,26 см², h= 21 см.

V = 21/6( 113,04 + 0 + 4* 28,26) = 791,28 см³

Задача № 5.

Вычисляем объём модели шара по обычной формуле. Для этого измеряем радиус шара R = 7 см. Вычисляем V =4/3(π *R³) = 4/3(3,14*343) = 1436 cм³

Вычисляем объем модели по формуле Симпсона V = h/6(Sнижнего основания + Sверхнего основания + 4Sсреднего сечения): площадь нижнего основания + 0, площадь верхнего основания = 0 и площадь среднего сечения S = π *R² = 3,14* 7² = 153,86 см², h= 2*R = 14 см.

V = 14/6(0 + 0 + 4*153,86) = 1436 см³

Вывод:

Объемы для каждой модели геометрических тел, найденные двумя способами, оказались равны. Формула Симпсона универсальна для таких тел, как пирамида, цилиндр, шар, куб и конус.

2.2 Практическое применение универсальной формулы

Цель: Показать применение формулы Симпсона в различных областях науки, сельском хозяйстве, производстве, а так же в различных жизненных ситуациях.

Объем ствола дерева

При строительстве, а также в разного рода житейских вопросах иногда бывает необходимо определить объем ствола дерева, вычислить, сколько в нем кубических метров древесины, а заодно и взвесить его. Оказывается, эта задача не так проста, как кажется; точного решения не существует, а довольствуются лишь приближенной оценкой. Даже для срубленного и очищенного от сучьев ствола дерева, задача разрешается далеко не просто. Объем ствола дерева более или менее близок либо к объему усеченного конуса, либо - для ствола дерева с вершинным концом - к объему полного конуса, либо, наконец, - для коротких бревен - к объему цилиндра. Но нельзя ли для расчета взять такую формулу объема, которая годилась бы сразу для всех трех названных тел?

Расчёт объема и массы ствола берёзы

Воспользуемся формулой Симпсона. Для этого понадобятся четыре измерения - длина ствола и площади трех оснований дерева: нижнего сруба, верхнего и среднего сечения. Если измерить бечевкой окружность ствола и разделить ее длину на число два пи, получим радиус. Высота березы(h) - 10 метров, а окружность ствола (L) на высоте груди и в основании ствола оказалась равной 1,2 м. R = L/(2 π).

S = π *R² - площадь соответствующих кругов равна 0,113 м ², а объем ствола по формуле Симпсона V = h/6(S_{нижнего основания} + S_{верхнего основания} + 4S_{среднего сечения}) V = 10/6(0,113 + 0 + 4*0,113) = 0,94 м³

Можно оценить и массу дерева на корню. Принимая, что 1 куб. метр свежей березовой древесины весит в среднем 670 кг, находим, что масса данной березы = 630 кг.

Вывод: Я располагаю формулой, по которой можно приближенно вычислить объем ствола дерева, не задаваясь вопросом о том, на какое геометрическое тело оно похоже: на цилиндр, на конус или на усеченный конус. Зная плотности различных пород древесины, можно вычислить массу дерева на корню.

Объем и масса сена

Для определения запасов корма каждому хозяйству необходимо оценить массу сена, уложенного в скирды и стога. Так как взвесить все скирды и стога невозможно, то для определения их массы находят объем, предварительно определив с помощью пробного взвешивания массу 1 м³ сена. На практике скирды и стога бывают довольно разнообразной формы, поэтому можно воспользоваться универсальной формулой Симпсона.

Объём помещения сложной формы

Вычислить объем помещения бывает нужно в самых разных ситуациях. Так, объем комнаты нужно знать при установке секционного радиатора отопления. Количество секций в нем прямо зависит от объемов комнаты. Если устанавливается кондиционер, также нужно знать объемы помещения, поскольку отдельный кондиционер предназначен только для конкретного объема помещения.

Объём емкостей сложной формы

Вычислить объем емкости, если нет под рукой измерительного цилиндра.

Измерение объемов сыпучих материалов

Точные замеры объемов складов и объемов перевозимых сыпучих и жидких материалов - это неотъемлемая часть работы горнорудных комбинатов, шахт, нефтеперерабатывающих заводов, химических производств, различных транспортных компаний и предприятий агропромышленного комплекса. Это касается тех производств, сырье или готовая продукция которых довольно сложно поддается точному учету. Речь, прежде всего, идет об учете сыпучих материалов: сельскохозяйственная продукция (зерно, клубни, подсолнечник), стройматериалы (песок, гравий, щебень, цемент), полезные ископаемые (уголь, руда).

Традиционным инструментом для определения объемов сыпучих материалов и грунта как при инвентаризации складов так и при земляных работах является обыкновенная геодезическая съемка или применения технологии 3D лазерного сканирования.

Этапы выполняемых работ: 3D лазерное сканирование объектов съемки (бурты, насыпи, котлованы, материалы на складах); построение 3D моделей объектов съемки; вычисление объемов объектов съемки.

Объем котлована

При расчете объема грунта, разрабатываемого при рытье котлована экскаватором, принимают ряд допущений, а именно: неровности дна и стен незначительны, форма котлована соответствует одной из геометрических фигур.

Объем воронки или ямы

Ликвидировать последствия стихии поможет формула Симпсона.

Конус выноса в геологии

В геологии существует понятие «конус выноса». Это форма рельефа, образованная скоплением обломочных пород (гальки, гравия, песка), вынесенными горными реками на предгорную равнину или в более плоскую широкую долину. Оценить масштабы поможет формула Симпсона.

Конус безопасности

По статистике на Земле ежегодно гибнет от разрядов молний 6 человек на 1000000 жителей. Этого бы не случалось, если бы везде были громоотводы, так как они образуется конус безопасности. Чем выше громоотвод, тем больше объем такого конуса.

Формула Симпсона так же применима в различных жизненных ситуациях. И такой пример применения описан в художественной литературе.

«Морской волчонок»

В романе "Морской волчонок" Майн Рид повествует о юном любителе морских приключений, который не имея средств заплатить за проезд, пробрался в трюм незнакомого корабля и здесь неожиданно оказался закупоренным на всё время морского перехода. Роясь в багаже, заполнявшем его темницу, он наткнулся на ящик сухарей и бочку воды. Ему необходимо было установить дневную порцию воды. Для этого нужно было узнать, сколько её содержится в бочке, и затем разделить на порции. Как мальчик вычислил объём бочки?

Вывод:

Проделав исследование, я доказала, что формула Симпсона универсальна для таких тел, как пирамида, цилиндр, шар, куб и конус.

Если форма тела имеет сложные геометрические конструкции, то для определения объема существует универсальная формула - формула Симпсона.

Из всей проделанной работы можно сделать вывод о том, что я располагаю формулой, по которой можно приближенно вычислить объем ствола дерева, воронки, стога сена, не задаваясь вопросом о том, на какое геометрическое тело оно похоже: на цилиндр или конус.

Теперь прогуливаясь по лесу, вам наверно будет, вероятно, интересно определить объём любого дерева. Вычислить сколько в нём кубических метров древесины, а заодно и взвесить его - зная плотность различных пород древесины, можно определить вес дерева на корню.

Формула Симпсона достаточно проста для запоминания, её стоит включить в школьную программу.

Список используемой литературы

1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия, 10-11 : Учеб. для общеобразоват. учреждений - 13-ое изд. - М.: Просвещение, 2007.- 206 с.

2. Геометрические фигуры. geometricheskie.narod.ru

3. www.ru.wikipedia.org Геометрия

4. Перельман Я.И; А.Л. Бондаренко. Геометрия на вольном воздухе.- М.: АСТ: Астрель; Владимир: ВКТ, 2008.- 94,[2] c.

Электронный адрес: www.ast.ru

5. e-science.ru/

6. www.freesession.ru/

</