- Учителю
- Дидактический материал по математике для работы с учащимися с ОВЗ 7, 8, 9 классов
Дидактический материал по математике для работы с учащимися с ОВЗ 7, 8, 9 классов
7класс
КАРТОЧКА № 1. Раскрытие скобок ВАРИАНТ 1
ПРАВИЛА
ОБРАЗЦЫ
ЗАДАНИЯ
Если перед скобкой стоит знак «плюс» или не стоит никакой знак, то можно убрать скобки, сохраняя знаки всех слагаемых, стоящих
внутри скобок.
(a - b + c) = a - b + c
+(x + y - z) = x + y - z
+(-a + c - 1) = -a + c - 1
Раскрыть скобки:
1) (x + y - z) - 1;
2) (x + y) - x;
3) (x + y) + (x - y);
4) (x + y) - (x - y);
5) (x - y + z) - (x + y - z).
Если перед скобкой стоит знак «минус», то можно убрать скобки, меняя знаки всех слагаемых, стоящих внутри скобок, на противоположные.
- (a - x + c) = - a + x - c
- (1 - x + a) = - 1 + x - a
КАРТОЧКА № 2. Умножение многочленов ВАРИАНТ 1
ПРАВИЛО
ОБРАЗЕЦ
ЗАДАНИЕ
Чтобы умножить многочлен на многочлен, умножь каждое слагаемое первого многочлена на каждое слагаемое второго многочлена.
(a + b - c)(x - y) =
= ax - ay + bx - by - cx + cy
Преобразовать произведение в многочлен:
1) (a + b)(c + d);
2) (a + 2)(b - c);
3) (a - 1)(a + b - 2);
4) (a - b)(a + b);
5) (a + b)(a + b).
КАРТОЧКА № 3. Разложение многочлена на множители вынесением за скобки общего множителя ВАРИАНТ 1
ПРАВИЛО
ОБРАЗЕЦ
ЗАДАНИЕ
Если у всех членов многочлена есть общий множитель, его можно вынести за скобки; в скобках нужно записать частные от деления каждого члена на этот множитель.
ax + ay - a = a(x + y - 1)
Преобразовать произведение в многочлен:
1) 2x - 2y;
2) 3x2 - 2x;
3) 3xy + 4xz;
4) 6xy - 3xz + 9x2;
5) (x - 1)a + 2(x - 1)c.
КАРТОЧКА № 4. Cвойства степени с натуральным показателем ВАРИАНТ 1
ФОРМУЛЫ
ОБРАЗЕЦ
ЗАДАНИЕ
1) am ∙ an = a m + n;
2) am : an = a m - n; если а ≠ 0 и m>n;
3) (ab)m = am∙ bm;
4) ![]() если b ≠ 0;
если b ≠ 0;
5) (am)n = amn.
22∙23 = 25 = 2∙2∙2∙2∙2 = 32;
37: 35 = 32 =3∙ 3 = 9, так как 3≠ 0 и 7>5;
6m = (2∙ 3)m = 2m∙ 3m;
![]()
(3m)2 = 32m.
Выбрать нужные формулы и с их помощью упростите выражения:
1) 531: 529;
2) (х2)3;
3) (2х)4;
4) (8х)5: (4х)5;
5) х3 х2.
КАРТОЧКА № 5. Формула квадрата суммы ВАРИАНТ 1
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
(I + II)2 = I2 + 2∙ I∙ II + II2
(a + b)2 = a2 + 2ab + b2
(3x + 4)2 = ?
I = 3x, II = 4;
I2 = (3x)2, 2∙I∙ II = 2∙ 3x∙ 4,
II2 = 42;
(3x + 4)2 = (3x)2 + 2∙3x∙4 + 42 = = 9x2 + 24x + 16.
Преобразовать выражение по данной формуле, если это возможно:
1) (a + b) 2;
2) x2 + 2xy + y2;
3) m2+ 3mn + n2;
4) (2n + 3)2;
5) a2 + 4a + 4.
I2 + 2∙ I∙ II + II2 = (I + II)2
a2 + 2ab + b2 = (a + b)2
25x2 + 10xy + y2 = ?
I2 = 25x2 = (5x)2, I = 5x, II2 = y2, II = y, 2∙ I∙ II = 10xy = 2∙5x∙ y,
25x2 + 10xy + y2 = (5x + y)2
КАРТОЧКА № 6. Формула квадрата разности ВАРИАНТ 1
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
(I - II)2 = I2 - 2∙ I∙ II + II2
(a - b)2 = a2 - 2ab + b2
(3x - 4)2 = ?
I = 3x, II = 4;
I2 = (3x)2, 2∙I∙ II = 2∙ 3x∙ 4,
II2 = 42;
(3x - 4)2 = (3x)2 - 2∙3x∙4 + 42 = = 9x2 - 24x + 16.
Преобразовать выражение по данной формуле, если это возможно:
1) (a - b) 2;
2) x2 - 2xy + y2;
3) m2 - 3mn + n2;
4) (2n - 3)2;
5) a2 - 4a + 4.
I2 - 2∙ I∙ II + II2 = (I - II)2
a2 - 2ab + b2 = (a - b)2
25x2 - 10xy + y2 = ?
I2 = 25x2 = (5x)2, I = 5x, II2 = y2, II = y, 2∙ I∙ II = 10xy = 2∙5x∙ y,
25x2 - 10xy + y2 = (5x - y)2
КАРТОЧКА № 7. Формула разности квадратов ВАРИАНТ 1
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
(I - II)(I + II) = I2 - II2
(a - b)(a + b) = a2 - b2
(2x - 3y)(2x + 3y) = ?
I = 2x, II = 3y;
I2 = (2x)2= 4x2, II2 = (3y)2= 9y2;
(2x - 3y)(2x + 3y) =(2x)2 -(3y)2 = = 4x2 - 9y2.
Преобразовать выражение по данной формуле, если это возможно:
1) (x - y) (x + y);
2) a2 - c2;
3) (10 - a)(10 + a);
4) p2 + q2;
5) 25m2 - 16n2.
I2 - II2 = (I - II)(I + II)
a2 - b2 = (a - b)(a + b)
a2 - 25 = ?
I2 = a2, I = a, II2 = 25 = 52, II = 5,
a2 - 25 = (a - 5)(a + 5)
КАРТОЧКА № 8. Решение линейных уравнений ВАРИАНТ 1
ПРАВИЛО
ОБРАЗЕЦ
ЗАДАНИЕ
Чтобы решить линейное уравнение, надо:
1) раскрыть скобки, если они имеются;
2) перенеси слагаемые с неизвестным в левую часть уравнения, меняя их знаки на противоположные;
3) перенеси слагаемые без неизвестного в правую часть уравнения, меняя их знаки на противоположные;
4) приведи в обеих частях подобные слагаемые;
5) раздели обе части уравнения на коэффициент при х (если он не равен нулю).
Решить уравнение:
2х - 17 = 63 + 4х.
Решение:
1) 2х - 17 - 4х =63;
2) 2х - 4х = 63 + 17;
3) - 2х = 80;
4)х = 80 : ( - 2) = - 40.
Ответ: - 40.
Решите уравнения:
1) 4х + 5 = 2х - 7;
2) 5х - 7 = 13;
3) 3(х + 2) = 2(х + 2);
4) 2х - 4 = 8 + 2х;
5) 4х + 6 = 2(2х + 3).
КАРТОЧКА № 1. Раскрытие скобок ВАРИАНТ 2
ПРАВИЛА
ОБРАЗЦЫ
ЗАДАНИЯ
Если перед скобкой стоит знак «плюс» или не стоит никакой знак, то можно убрать скобки, сохраняя знаки всех слагаемых, стоящих
внутри скобок.
(a - b + c) = a - b + c
+(x + y - z) = x + y - z
+(-a + c - 1) = -a + c - 1
Раскрыть скобки:
1) (a + b - c) + 2;
2) a + ( b - c);
3) a - (a - b + c);
4) (x - y) - (x + y);
5) (a - b + 1) - (a + b - 1).
Если перед скобкой стоит знак «минус», то можно убрать скобки, меняя знаки всех слагаемых, стоящих внутри скобок, на противоположные.
- (a - x + c) = - a + x - c
- (1 - x + a) = - 1 + x - a
КАРТОЧКА № 2. Умножение многочленов ВАРИАНТ 2
ПРАВИЛО
ОБРАЗЕЦ
ЗАДАНИЕ
Чтобы умножить многочлен на многочлен, умножь каждое слагаемое первого многочлена на каждое слагаемое второго многочлена.
(a + b - c)(x - y) =
= ax - ay + bx - by - cx + cy
Преобразовать произведение в многочлен:
1) (x + y)(z + t);
2) (x + 2)(y - z;
3) (x - 1)(x + y - 3);
4) (x - y)(x + y);
5) (x + y)(x + y).
КАРТОЧКА № 3. Разложение многочлена на множители вынесением за скобки общего множителя ВАРИАНТ 2
ПРАВИЛО
ОБРАЗЕЦ
ЗАДАНИЕ
Если у всех членов многочлена есть общий множитель, его можно вынести за скобки; в скобках нужно записать частные от деления каждого члена на этот множитель.
ax + ay - a = a(x + y - 1)
Преобразовать произведение в многочлен:
1) 3a - 3b;
2) 7a2 - 3ax;
3) 2ac + 5bc;
4) 6ad + 2cd - 4d2;
5) (a + 2)x + 3(a + 2)y.
КАРТОЧКА № 4. Cвойства степени с натуральным показателем ВАРИАНТ 2
ФОРМУЛЫ
ОБРАЗЕЦ
ЗАДАНИЕ
1) am ∙ an = a m + n;
2) am : an = a m - n; если а ≠ 0 и m>n;
3) (ab)m = am∙ bm;
4) ![]() если b ≠ 0;
если b ≠ 0;
5) (am)n = amn.
22∙23 = 25 = 2∙2∙2∙2∙2 = 32;
37: 35 = 32 =3∙ 3 = 9, так как 3≠ 0 и 7>5;
6m = (2∙ 3)m = 2m∙ 3m;
![]()
(3m)2 = 32m.
Выбрать нужные формулы и с их помощью упростите выражения:
1) 711: 79;
2) (а3)2;
3) (3а)5;
4) (6а)4: (3а)4;
5) у4 у.
КАРТОЧКА № 5. Формула квадрата суммы ВАРИАНТ 2
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
(I + II)2 = I2 + 2∙ I∙ II + II2
(a + b)2 = a2 + 2ab + b2
(3x + 4)2 = ?
I = 3x, II = 4;
I2 = (3x)2, 2∙I∙ II = 2∙ 3x∙ 4,
II2 = 42;
(3x + 4)2 = (3x)2 + 2∙3x∙4 + 42 = = 9x2 + 24x + 16.
Преобразовать выражение по данной формуле, если это возможно:
1) (x + y) 2;
2) a2 + 2ab + b2;
3) p2+ 4pq + q2;
4) (2 + 3k)2;
5) a2 + 6a + 9.
I2 + 2∙ I∙ II + II2 = (I + II)2
a2 + 2ab + b2 = (a + b)2
25x2 + 10xy + y2 = ?
I2 = 25x2 = (5x)2, I = 5x, II2 = y2, II = y, 2∙ I∙ II = 10xy = 2∙5x∙ y,
25x2 + 10xy + y2 = (5x + y)2
КАРТОЧКА № 6. Формула квадрата суммы ВАРИАНТ 2
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
(I - II)2 = I2 - 2∙ I∙ II + II2
(a - b)2 = a2 - 2ab + b2
(3x - 4)2 = ?
I = 3x, II = 4;
I2 = (3x)2, 2∙I∙ II = 2∙ 3x∙ 4,
II2 = 42;
(3x - 4)2 = (3x)2 - 2∙3x∙4 + 42 = = 9x2 - 24x + 16.
Преобразовать выражение по данной формуле, если это возможно:
1) (x - y) 2;
2) a2 - 2ab + b2;
3) p2 - 4pq + q2;
4) (2 - 3k)2;
5) a2 - 6a + 9.
I2 - 2∙ I∙ II + II2 = (I - II)2
a2 - 2ab + b2 = (a - b)2
25x2 - 10xy + y2 = ?
I2 = 25x2 = (5x)2, I = 5x, II2 = y2, II = y, 2∙ I∙ II = 10xy = 2∙5x∙ y,
25x2 - 10xy + y2 = (5x - y)2
КАРТОЧКА № 7. Формула разности квадратов ВАРИАНТ 2
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
(I - II)(I + II) = I2 - II2
(a - b)(a + b) = a2 - b2
(2x - 3y)(2x + 3y) = ?
I = 2x, II = 3y;
I2 = (2x)2= 4x2, II2 = (3y)2= 9y2;
(2x - 3y)(2x + 3y) =(2x)2 -(3y)2 = = 4x2 - 9y2.
Преобразовать выражение по данной формуле, если это возможно:
1) (a - b) (a + b);
2) 4a2 - 1;
3) (3t - 2)(3t + 2);
4) x2 + 4;
5) 9k2 - 49.
I2 - II2 = (I - II)(I + II)
a2 - b2 = (a - b)(a + b)
a2 - 25 = ?
I2 = a2, I = a, II2 = 25 = 52, II = 5,
a2 - 25 = (a - 5)(a + 5)
КАРТОЧКА № 8. Решение линейных уравнений ВАРИАНТ 2
ПРАВИЛО
ОБРАЗЕЦ
ЗАДАНИЕ
Чтобы решить линейное уравнение, надо:
1) раскрыть скобки, если они имеются;
2) перенеси слагаемые с неизвестным в левую часть уравнения, меняя их знаки на противоположные;
3) перенеси слагаемые без неизвестного в правую часть уравнения, меняя их знаки на противоположные;
4) приведи в обеих частях подобные слагаемые;
5) раздели обе части уравнения на коэффициент при х (если он не равен нулю).
Решить уравнение:
2х - 17 = 63 + 4х.
Решение:
1) 2х - 17 - 4х =63;
2) 2х - 4х = 63 + 17;
3) - 2х = 80;
4)х = 80 : ( - 2) = - 40.
Ответ: - 40.
Решите уравнения:
1) 3х + 4 = 7х - 8;
2) 2х - 3 = 10;
3) 2(х + 1) = 3(х + 1);
4) 3х - 5 = 3 + 3х;
5) 3х + 6 = 3( х + 2).
КАРТОЧКА № 1. Раскрытие скобок ВАРИАНТ 3
ПРАВИЛА
ОБРАЗЦЫ
ЗАДАНИЯ
Если перед скобкой стоит знак «плюс» или не стоит никакой знак, то можно убрать скобки, сохраняя знаки всех слагаемых, стоящих
внутри скобок.
(a - b + c) = a - b + c
+(x + y - z) = x + y - z
+(-a + c - 1) = -a + c - 1
Раскрыть скобки:
1) (m + p - q) - p;
2) m + ( p - q);
3) m - (m - p + q);
4) (p + q) - (p - q);
5) (m - p + 5) - (m + p - 3).
Если перед скобкой стоит знак «минус», то можно убрать скобки, меняя знаки всех слагаемых, стоящих внутри скобок, на противоположные.
- (a - x + c) = - a + x - c
- (1 - x + a) = - 1 + x - a
КАРТОЧКА № 2. Умножение многочленов ВАРИАНТ 3
ПРАВИЛО
ОБРАЗЕЦ
ЗАДАНИЕ
Чтобы умножить многочлен на многочлен, умножь каждое слагаемое первого многочлена на каждое слагаемое второго многочлена.
(a + b - c)(x - y) =
= ax - ay + bx - by - cx + cy
Преобразовать произведение в многочлен:
1) (m + n)(p + q);
2) (m + 2)(n - p);
3) (m - 1)(m + n - 2);
4) (m - p)(m + p);
5) (m + 2)(m + 2).
КАРТОЧКА № 3. Разложение многочлена на множители вынесением за скобки общего множителя ВАРИАНТ 3
ПРАВИЛО
ОБРАЗЕЦ
ЗАДАНИЕ
Если у всех членов многочлена есть общий множитель, его можно вынести за скобки; в скобках нужно записать частные от деления каждого члена на этот множитель.
ax + ay - a = a(x + y - 1)
Преобразовать произведение в многочлен:
1) 4p - 4q;
2) q2 - 7p;
3) pq + 2mp;
4) 6ay - 3az + 9a2;
5) (m + 1)a + 4(m + 1)b.
КАРТОЧКА № 4. Cвойства степени с натуральным показателем ВАРИАНТ 3
ФОРМУЛЫ
ОБРАЗЕЦ
ЗАДАНИЕ
1) am ∙ an = a m + n;
2) am : an = a m - n; если а ≠ 0 и m>n;
3) (ab)m = am∙ bm;
4) ![]() если b ≠ 0;
если b ≠ 0;
5) (am)n = amn.
22∙23 = 25 = 2∙2∙2∙2∙2 = 32;
37: 35 = 32 =3∙ 3 = 9, так как 3≠ 0 и 7>5;
6m = (2∙ 3)m = 2m∙ 3m;
![]()
(3m)2 = 32m.
Выбрать нужные формулы и с их помощью упростите выражения:
1) 618: 617;
2) (b4)3;
3) (2m)3;
4) (10n)6: (5n)6;
5) a a4.
КАРТОЧКА № 5. Формула квадрата суммы ВАРИАНТ 3
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
(I + II)2 = I2 + 2∙ I∙ II + II2
(a + b)2 = a2 + 2ab + b2
(3x + 4)2 = ?
I = 3x, II = 4;
I2 = (3x)2, 2∙I∙ II = 2∙ 3x∙ 4,
II2 = 42;
(3x + 4)2 = (3x)2 + 2∙3x∙4 + 42 = = 9x2 + 24x + 16.
Преобразовать выражение по данной формуле, если это возможно:
1) (c + d) 2;
2) x2 + 2x + 1;
3) a2+ 8a + 16;
4) (2p + q)2;
5) 4a2 + 4a + 1.
I2 + 2∙ I∙ II + II2 = (I + II)2
a2 + 2ab + b2 = (a + b)2
25x2 + 10xy + y2 = ?
I2 = 25x2 = (5x)2, I = 5x, II2 = y2, II = y, 2∙ I∙ II = 10xy = 2∙5x∙ y,
25x2 + 10xy + y2 = (5x + y)2
КАРТОЧКА № 6. Формула квадрата суммы ВАРИАНТ 3
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
(I - II)2 = I2 - 2∙ I∙ II + II2
(a - b)2 = a2 - 2ab + b2
(3x - 4)2 = ?
I = 3x, II = 4;
I2 = (3x)2, 2∙I∙ II = 2∙ 3x∙ 4,
II2 = 42;
(3x - 4)2 = (3x)2 - 2∙3x∙4 + 42 = = 9x2 - 24x + 16.
Преобразовать выражение по данной формуле, если это возможно:
1) (c - d) 2;
2) x2 - 2x + 1;
3) a2 - 8a + 16;
4) (2p - q)2;
5) 4a2 - 4a + 1.
I2 - 2∙ I∙ II + II2 = (I - II)2
a2 - 2ab + b2 = (a - b)2
25x2 - 10xy + y2 = ?
I2 = 25x2 = (5x)2, I = 5x, II2 = y2, II = y, 2∙ I∙ II = 10xy = 2∙5x∙ y,
25x2 - 10xy + y2 = (5x - y)2
КАРТОЧКА № 7. Формула разности квадратов ВАРИАНТ 3
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
(I - II)(I + II) = I2 - II2
(a - b)(a + b) = a2 - b2
(2x - 3y)(2x + 3y) = ?
I = 2x, II = 3y;
I2 = (2x)2= 4x2, II2 = (3y)2= 9y2;
(2x - 3y)(2x + 3y) =(2x)2 -(3y)2 = = 4x2 - 9y2.
Преобразовать выражение по данной формуле, если это возможно:
1) (c - d) (c + d);
2) 100 - x2;
3) (3 - q)3 + q);
4) 1 + x2;
5) m2 - 4.
I2 - II2 = (I - II)(I + II)
a2 - b2 = (a - b)(a + b)
a2 - 25 = ?
I2 = a2, I = a, II2 = 25 = 52, II = 5,
a2 - 25 = (a - 5)(a + 5)
КАРТОЧКА № 8. Решение линейных уравнений ВАРИАНТ 3
ПРАВИЛО
ОБРАЗЕЦ
ЗАДАНИЕ
Чтобы решить линейное уравнение, надо:
1) раскрыть скобки, если они имеются;
2) перенеси слагаемые с неизвестным в левую часть уравнения, меняя их знаки на противоположные;
3) перенеси слагаемые без неизвестного в правую часть уравнения, меняя их знаки на противоположные;
4) приведи в обеих частях подобные слагаемые;
5) раздели обе части уравнения на коэффициент при х (если он не равен нулю).
Решить уравнение:
2х - 17 = 63 + 4х.
Решение:
1) 2х - 17 - 4х =63;
2) 2х - 4х = 63 + 17;
3) - 2х = 80;
4)х = 80 : ( - 2) = - 40.
Ответ: - 40.
Решите уравнения:
1) 5х + 1 = 3х + 7;
2) 6х - 1 = 11;
3) х - 1 = 7(х - 1);
4) х - 2 = 1 + 4х;
5) 5х + 5 = 5(х - 1).
8класс
Карточка 1 Основное свойство дроби
Правило
Образцы
Задания ( Вариант 1)
Сократить дробь:![]() ,
,
где ![]()
-
Сократить дробь:
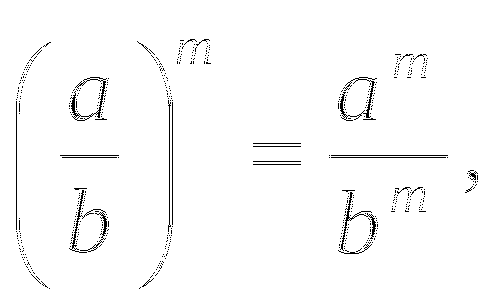
-
Сократить дробь:
![]()
-
Привести дробь
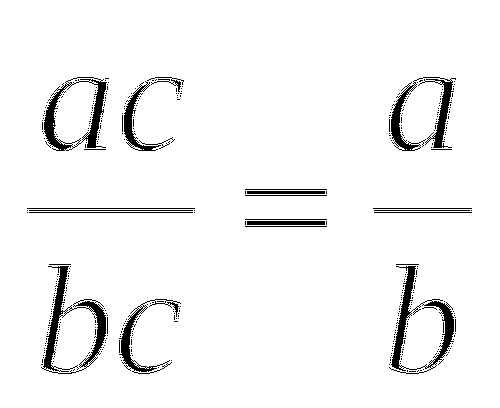 к знаменателю х2 - у2.
к знаменателю х2 - у2.
![]()
Сократить дроби:
1) ![]() 2)
2)![]() 3)
3)![]()
Указание: в заданиях 2) и 3) используй формулы сокращённого умножения: (а-b)(a+b) = a2 - b2 ,
a2 - 2ab + b2 = (a - b)2 или a2 + 2ab + b2 = (a +b)2.
Привести дроби к общему знаменателю:
4) ![]() и
и ![]() 5)
5) ![]() и
и ![]()
Привести дробь к новому знаменателю:
![]()
Карточка 1 Основное свойство дроби
Правило
Образцы
Задания ( Вариант 2)
Сократить дробь:![]() ,
,
где ![]()
1)Сократить дробь:![]()
2)Сократить дробь:
![]()
3)Привести дробь ![]() к знаменателю х2 - у2.
к знаменателю х2 - у2.
![]()
Сократить дроби:
1) ![]() 2)
2)![]() 3)
3)![]()
Указание: в заданиях 2) и 3) используй формулы сокращённого умножения: (а-b)(a+b) = a2 - b2 ,
a2 - 2ab + b2 = (a - b)2 или a2 + 2ab + b2 = (a +b)2.
Привести дроби к общему знаменателю:
4) ![]() и
и ![]() 5)
5) ![]() и
и ![]()
Привести дробь к новому знаменателю:
![]()
Карточка 1 Основное свойство дроби
Правило
Образцы
Задания ( Вариант 3)
Сократить дробь:![]() ,
,
где ![]()
1)Сократить дробь:![]()
2)Сократить дробь:
![]()
3)Привести дробь ![]() к знаменателю х2 - у2.
к знаменателю х2 - у2.
![]()
Сократить дроби:
1) ![]() 2)
2)![]() 3)
3)![]()
Указание: в заданиях 2) и 3) используй формулы сокращённого умножения: (а-b)(a+b) = a2 - b2 ,
a2 - 2ab + b2 = (a - b)2 или a2 + 2ab + b2 = (a +b)2.
Привести дроби к общему знаменателю:
4) ![]() и
и ![]() 5)
5) ![]() и
и ![]()
Привести дробь к новому знаменателю:
![]()
Карточка 2 Сложение и вычитание дробей с одинаковыми знаменателями
Правило
Образцы
Задания ( Вариант 1)
![]() ,
,
где b ≠ 0
![]() ,
,
где b ≠ 0
1) ![]()
2) ![]()
Указание: 2) в последнем шаге надо разложить знаменатель на множители по формуле c2 - d2 = (c - d)(c + d) и сократить дробь на c - d.
Найти суммы и разности:
1) ![]() 2)
2)![]() 3)
3)![]() 4)
4) ![]() 5)
5) ![]() ;
;
Указание: в заданиях 3), 4) и 5) используй в последнем шаге формулы сокращённого умножения: (а-b)(a+b) = a2 - b2 , a2 - 2ab + b2 = (a - b)2 или a2 + 2ab + b2 = (a +b)2.
Карточка 2 Сложение и вычитание дробей с одинаковыми знаменателями
Правило
Образцы
Задания ( Вариант 2)
![]() ,
,
где b ≠ 0
![]() ,
,
где b ≠ 0
1) ![]()
2) ![]()
Указание: 2) в последнем шаге надо разложить знаменатель на множители по формуле c2 - d2 = (c - d)(c + d) и сократить дробь на c - d.
Найти суммы и разности:
1) ![]() 2)
2)![]() 3)
3)![]() 4)
4) ![]() 5)
5) ![]() .
.
Указание: в заданиях 3), 4) и 5) используй в последнем шаге формулы сокращённого умножения: (а-b)(a+b) = a2 - b2 , a2 - 2ab + b2 = (a - b)2 или a2 + 2ab + b2 = (a +b)2.
Карточка 2 Сложение и вычитание дробей с одинаковыми знаменателями
Правило
Образцы
Задания ( Вариант 3)
![]() ,
,
где b ≠ 0
![]() ,
,
где b ≠ 0
1) ![]()
2) ![]()
Указание: 2) в последнем шаге надо разложить знаменатель на множители по формуле c2 - d2 = (c - d)(c + d) и сократить дробь на c - d.
Найти суммы и разности:
1) ![]() 2)
2)![]() 3)
3)![]() 4)
4) ![]() 5)
5) ![]() .
.
Указание: в заданиях 3), 4) и 5) используй в последнем шаге формулы сокращённого умножения: (а-b)(a+b) = a2 - b2 , a2 - 2ab + b2 = (a - b)2 или a2 + 2ab + b2 = (a +b)2.
Карточка 3 Сложение и вычитание дробей с разными знаменателями
Правило
Образцы
Задания ( Вариант 1)
![]() ,
,
где b,d ≠ 0
1) найдите общий зна -менатель, состоящий из произведения всех различных выражений;
2) умножить числитель и знаменатель каждой дроби на их дополнительный множитель;
3)выполнить действия.
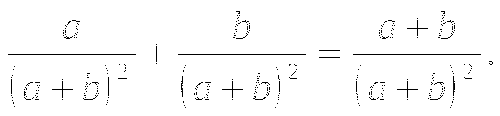
Общий знаменатель: (а - b)2(а + b). Дополнительный множитель для первой дроби - это (a + b) , для второй дроби - это (а - b)
Указание: при составлении общего знаменателя из всех степеней берут степень с наибольшим показателем; в нашем случае это (а - b)2
Найти суммы и разности:
1) ![]() 2)
2)![]() 3)
3)![]() 4)
4) ![]() 5)
5) ![]() .
.
Указание: в задании 2) знаменатели -противоположные выражения, в задании 5) надо вначале разложить на множители каждый знаменатель, используя ФСУ,а затем составить общий знаменатель.
ФСУ: a2 - b2 =(а-b)(a+b) , (a - b)2 = a2 - 2ab + b2, (a +b)2 = a2 + 2ab + b2
Карточка 3 Сложение и вычитание дробей с разными знаменателями
Правило
Образцы
Задания ( Вариант 2)
![]() ,
,
где b,d ≠ 0
1) найдите общий зна -менатель, состоящий из произведения всех различных выражений;
2) умножить числитель и знаменатель каждой дроби на их дополнительный множитель;
3)выполнить действия.
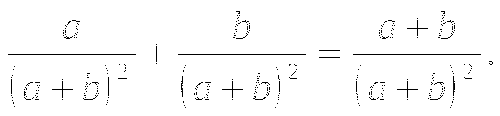
Общий знаменатель: (а - b)2(а + b). Дополнительный множитель для первой дроби - это (a + b) , для второй дроби - это (а - b)
Указание: при составлении общего знаменателя из всех степеней берут степень с наибольшим показателем; в нашем случае это (а - b)2
Найти суммы и разности:
1) ![]() 2)
2)![]() 3)
3)![]() 4)
4) ![]() 5)
5) ![]() .
.
Указание: в задании 2) знаменатели -противоположные выражения, в задании 5) надо вначале разложить на множители каждый знаменатель, используя ФСУ,а затем составить общий знаменатель.
ФСУ: a2 - b2 =(а-b)(a+b) , (a - b)2 = a2 - 2ab + b2, (a +b)2 = a2 + 2ab + b2
Карточка 3 Сложение и вычитание дробей с разными знаменателями
Правило
Образцы
Задания ( Вариант 3)
![]() ,
,
где b,d ≠ 0
1) найдите общий зна -менатель, состоящий из произведения всех различных выражений;
2) умножить числитель и знаменатель каждой дроби на их дополнительный множитель;
3)выполнить действия.
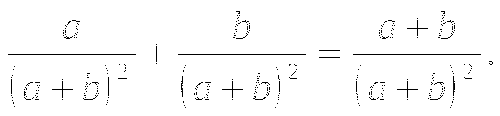
Общий знаменатель: (а - b)2(а + b). Дополнительный множитель для первой дроби - это (a + b) , для второй дроби - это (а - b)
Указание: при составлении общего знаменателя из всех степеней берут степень с наибольшим показателем; в нашем случае это (а - b)2
Найти суммы и разности:
1) ![]() 2)
2)![]() 3)
3)![]() 4)
4) ![]() 5)
5) ![]() .
.
Указание: в задании 2) знаменатели -противоположные выражения, в задании 5) надо вначале разложить на множители каждый знаменатель, используя ФСУ,а затем составить общий знаменатель.
ФСУ: a2 - b2 =(а-b)(a+b) , (a - b)2 = a2 - 2ab + b2, (a +b)2 = a2 + 2ab + b2
Карточка 4 Умножение дробей. Возведение дроби в степень
Правило
Образцы
Задания ( Вариант 1)
![]() ,
,
где b,d ≠ 0
![]() ,
,
где b ≠ 0 или
![]()
1)Выполни умножение:
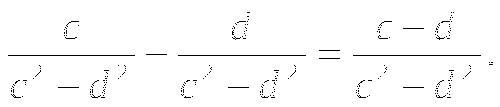
2) ![]()
3) ![]() Указание: В задании 1)и 2) вначале разложите числители и знаменатели на множители, а затем сократите дроби
Указание: В задании 1)и 2) вначале разложите числители и знаменатели на множители, а затем сократите дроби
Найти произведение дробей:
1) ![]() 2)
2) ![]()
3) ![]()
4)![]()
Вычислить: ![]()
Указание: В задании 3) и 4) вначале разложите числители и знаменатели на множители, вынеся общий множитель за скобки, а затем сократите дроби
Карточка 4 Умножение дробей. Возведение дроби в степень
Правило
Образцы
Задания ( Вариант 2)
![]() ,
,
где b,d ≠ 0
![]() ,
,
где b ≠ 0 или
![]()
1)Выполни умножение:

2) ![]()
3) ![]() Указание: В задании 1) и 2) вначале разложите числители и знаменатели на множители, а затем сократите дроби
Указание: В задании 1) и 2) вначале разложите числители и знаменатели на множители, а затем сократите дроби
Найти произведение дробей:
1) ![]() 2)
2) ![]()
3) ![]()
4)![]()
Вычислить: ![]()
Указание: В задании 3) и 4) вначале разложите числители и знаменатели на множители, вынеся общий множитель за скобки, а затем сократите дроби
Карточка 4 Умножение дробей. Возведение дроби в степень
Правило
Образцы
Задания ( Вариант 3)
![]() ,
,
где b,d ≠ 0
![]() ,
,
где b ≠ 0 или
![]()
1)Выполни умножение:

2) ![]()
3) ![]() Указание: В задании 1)и 2) вначале разложите числители и знаменатели на множители, а затем сократите дроби
Указание: В задании 1)и 2) вначале разложите числители и знаменатели на множители, а затем сократите дроби
Найти произведение дробей:
1) ![]() 2)
2) ![]()
3) ![]()
4)![]()
Вычислить: ![]()
Указание: В задании 3) и 4) вначале разложите числители и знаменатели на множители, вынеся общий множитель за скобки, а затем сократите дроби
Карточка 5 Деление дробей
Правило
Образцы
Задания ( Вариант 1)
![]() ,
,
где b,с,d ≠ 0
Выполнить деление:
1) 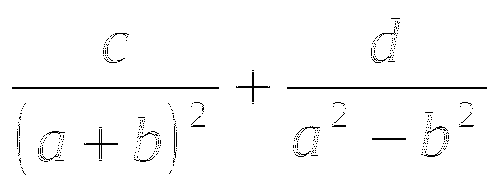
2) ![]()
Указание: В задании 1) вначале разложите числители и знаменатели на множители, используя вынесение общего множителя за скобки и формулы сокращённого умножения(ФСУ), а затем сократите дробь
ФСУ: х2 - у2 = (х - у)(х + у)
Найти частное дробей:
1) ![]() 2)
2)![]()
3) ![]()
4)![]()
5) ![]()
Указание: В задании 3),4),5) вначале разложите числители и знаменатели на множители, вынеся общий множитель за скобки и используя ФСУ, а затем сократите дроби
Карточка 5 Деление дробей
Правило
Образцы
Задания ( Вариант 2)
![]() ,
,
где b,с,d ≠ 0
Выполнить деление:
1) 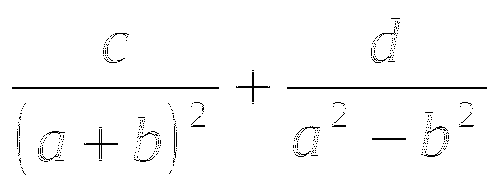
2) ![]()
Указание: В задании 1) вначале разложите числители и знаменатели на множители, используя вынесение общего множителя за скобки и формулы сокращённого умножения(ФСУ), а затем сократите дробь
ФСУ: х2 - у2 = (х - у)(х + у)
Найти частное дробей:
1) ![]() 2)
2)![]()
3) ![]()
4)![]()
5) ![]()
Указание: В задании 3),4),5) вначале разложите числители и знаменатели на множители, вынеся общий множитель за скобки и используя ФСУ, а затем сократите дроби
Карточка 5 Деление дробей
Правило
Образцы
Задания ( Вариант 3)
![]() ,
,
где b,с,d ≠ 0
Выполнить деление:
1) 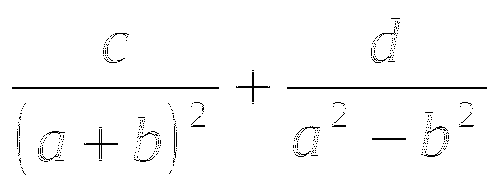
2) ![]()
Указание: В задании 1) вначале разложите числители и знаменатели на множители, используя вынесение общего множителя за скобки и формулы сокращённого умножения(ФСУ), а затем сократите дробь
ФСУ: a2 - b2 = (a - b)(a + b)
a3 - b3 = (a - b)(a2 + ab + b2)
a4 - b4 = (a2 - b2)(a2 + b2) = (a - b)(a + b) a2 + b2)
Найти частное дробей:
1) ![]() 2)
2)![]()
3) ![]()
4)![]()
5) ![]()
Указание: В задании 3),4),5) вначале разложите числители и знаменатели на множители, вынеся общий множитель за скобки и используя ФСУ, а затем сократите дроби
Карточка 6 Свойства квадратных корней
Правила
Образцы
Задания ( Вариант 1)
![]()
если ![]() .
.
![]() если
если ![]() , b > 0.
, b > 0.
![]()
![]() , если
, если ![]() .
.
Вычислить:
1)![]()
2)![]() ;
;
3)![]()
4)![]()
Вычислите:
1)![]() ;
;
2)![]() ;
;
3)![]() ;
;
4) ![]() ;
;
5)![]() .
.
Карточка 6 Свойства квадратных корней
Правила
Образцы
Задания ( Вариант 2)
![]()
если ![]() .
.
![]() если
если ![]() , b > 0.
, b > 0.
![]()
![]() , если
, если ![]() .
.
Вычислить:
1)![]()
2)![]() ;
;
3)![]()
4)![]()
Вычислите:
1)![]() ;
;
2)![]() ;
;
3)![]() ;
;
4) ![]() ;
;
5)![]() .
.
Карточка 6 Свойства квадратных корней
Правила
Образцы
Задания ( Вариант 3)
![]()
если ![]() .
.
![]() если
если ![]() , b > 0.
, b > 0.
![]()
![]() , если
, если ![]() .
.
Вычислить:
1)![]()
2)![]() ;
;
3)![]()
4)![]()
Вычислите:
1)![]() ;
;
2)![]() ;
;
3)![]() ;
;
4) ![]() ;
;
5)![]() .
.
Карточка 7 Вынесение множителя из - под знака корня
Правила
Образцы
Задания ( Вариант 1)
![]()
если ![]() .
.
![]()
1)![]() ;
;
2)![]() ;
;
3)![]() , т.к. у2 ≥ 0;
, т.к. у2 ≥ 0;
4) ![]()
Пояснения: т.к. по условию z7 ≥ 0, то z ≥ 0. Но тогда
![]() .
.
Вынести множитель из - под корня:
1)![]() ; 2)
; 2)![]() ;
;
3)![]() где х > 0,
где х > 0,
у< 0.
4) ![]() ; 5)
; 5)![]() .
.
Карточка 7 Вынесение множителя из - под знака корня
Правила
Образцы
Задания ( Вариант 2)
![]()
если ![]() .
.
![]()
1)![]() ;
;
2)![]() ;
;
3)![]() , т.к. у2 ≥ 0;
, т.к. у2 ≥ 0;
4) ![]()
Пояснения: т.к. по условию z7 ≥ 0, то z ≥ 0. Но тогда
![]() .
.
Вынести множитель из - под корня:
1)![]() ; 2)
; 2)![]() ;
;
3)![]() где d > 0, с< 0.
где d > 0, с< 0.
4) ![]() ; 5)
; 5)![]() .
.
Карточка 7 Вынесение множителя из - под знака корня
Правила
Образцы
Задания ( Вариант 3)
![]()
если ![]() .
.
![]()
1)![]() ;
;
2)![]() ;
;
3)![]() , т.к. у2 ≥ 0;
, т.к. у2 ≥ 0;
4) ![]()
Пояснения: т.к. по условию z7 ≥ 0, то z ≥ 0. Но тогда
![]() .
.
Вынести множитель из - под корня:
1)![]() ; 2)
; 2)![]() ;
;
3)![]() где q > 0,
где q > 0,
p< 0.
4) ![]() ; 5)
; 5)![]() .
.
Карточка 8 Внесение множителя под знак корня
Правила
Образцы
Задания ( Вариант 1)
Чтобы внести множитель под знак корня, нужно:
1)возвести его в квадрат;
2) если этот множитель отрицателен, изменить его знак при внесении под корень, а «минус» оставить перед корнем.
Заменить выражение ![]() квадратным корнем или выражением, ему противоположным:
квадратным корнем или выражением, ему противоположным:
а ≥ 0; ![]()
а ≤ 0; ![]()
Впервом случае получился квадратный корень, а во втором - выражение, противоположное квадратному корню
Заменить выражение квадратным корнем или выражением, ему противоположным:
1)![]() ; 2)
; 2)![]() ;
;
3)![]() где х > 0;
где х > 0;
4) ![]() ; 5)
; 5)![]() .
.
Карточка 8 Внесение множителя под знак корня
Правила
Образцы
Задания ( Вариант 2)
Чтобы внести множитель под знак корня, нужно:
1)возвести его в квадрат;
2) если этот множитель отрицателен, изменить его знак при внесении под корень, а «минус» оставить перед корнем.
Заменить выражение ![]() квадратным корнем или выражением, ему противоположным:
квадратным корнем или выражением, ему противоположным:
а ≥ 0; ![]()
а ≤ 0; ![]()
Впервом случае получился квадратный корень, а во втором - выражение, противоположное квадратному корню
Заменить выражение квадратным корнем или выражением, ему противоположным:
1)![]() ; 2)
; 2)![]() ;
;
3)![]() где у < 0;
где у < 0;
4) ![]() ; 5)
; 5)![]() .
.
Карточка 8 Внесение множителя под знак корня
Правила
Образцы
Задания ( Вариант 3)
Чтобы внести множитель под знак корня, нужно:
1)возвести его в квадрат;
2) если этот множитель отрицателен, изменить его знак при внесении под корень, а «минус» оставить перед корнем.
Заменить выражение ![]() квадратным корнем или выражением, ему противоположным:
квадратным корнем или выражением, ему противоположным:
а ≥ 0; ![]()
а ≤ 0; ![]()
Впервом случае получился квадратный корень, а во втором - выражение, противоположное квадратному корню
Заменить выражение квадратным корнем или выражением, ему противоположным:
1)![]() ; 2)
; 2)![]() ;
;
3)![]() ;
;
4) ![]() ; 5)
; 5)![]() .
.
Карточка 9 Решение неполных квадратных уравнений
Правила
Образцы
Задания ( Вариант 1)
Уравнение вида ах2 = 0
решается так:
ах2 = 0
х2 = 0(а ≠ 0)
х = 0.
Уравнение вида ах2+ bх = 0
решается так:
ах2+ bх = 0
х(ах + b) = 0
x = 0 или ax + b = 0
x = 0 или x = ![]() .
.
Уравнение вида ах2+ c = 0
решается так:
ах2+ c = 0, ax2 = -c,
![]() , где а ≠ 0;
, где а ≠ 0;
1)если ![]() , то корней нет;
, то корней нет;
2)если ![]() ,то х = 0;
,то х = 0;
3) если ![]() , то х =
, то х = ![]() .
.
Решить уравнения:
1) 2х2 + 8 = 0 - уравнение вида ах2+с=0;
2х2 = - 8,
х2 = -4. Ответ: корней нет
2) 3х2 - 2х = 0 - уравнение вида ах2+ bx =0.
3х2 - 2х = 0,
x(3x - 2) = 0,
x = 0 или 3x - 2 = 0,
x = 0 или ![]() . Ответ: 0;
. Ответ: 0; ![]()
3)7х2 - 8 = 0 - уравнение вида ах2 + с = 0.
7х2 - 8 = 0,
7х2 = 8,
х2 = ![]() ,
,
![]() . Ответ:
. Ответ: ![]()
4)6х2 = 0 - уравнение вида ах2 = 0.
6х2 = 0,
х2 = 0,
х = 0. Ответ: 0
1) 3х2 + 3 = 0;
2) -х2 + 5х = 0;
3) 7х2 - 28 = 0;
4) -х2 = 0;
5) 4(х - 1)2 - 16 = 0
Карточка 9 Решение неполных квадратных уравнений
Правила
Образцы
Задания ( Вариант 2)
Уравнение вида ах2 = 0
решается так:
ах2 = 0
х2 = 0(а ≠ 0)
х = 0.
Уравнение вида ах2+ bх = 0
решается так:
ах2+ bх = 0
х(ах + b) = 0
x = 0 или ax + b = 0
x = 0 или x = ![]() .
.
Уравнение вида ах2+ c = 0
решается так:
ах2+ c = 0, ax2 = -c,
![]() , где а ≠ 0;
, где а ≠ 0;
1)если ![]() , то корней нет;
, то корней нет;
2)если ![]() ,то х = 0;
,то х = 0;
3) если ![]() , то х =
, то х = ![]() .
.
Решить уравнения:
1) 2х2 + 8 = 0 - уравнение вида ах2+с=0;
2х2 = - 8,
х2 = -4. Ответ: корней нет
2) 3х2 - 2х = 0 - уравнение вида ах2+ bx =0.
3х2 - 2х = 0,
x(3x - 2) = 0,
x = 0 или 3x - 2 = 0,
x = 0 или ![]() . Ответ: 0;
. Ответ: 0; ![]()
3)7х2 - 8 = 0 - уравнение вида ах2 + с = 0.
7х2 - 8 = 0,
7х2 = 8,
х2 = ![]() ,
,
![]() . Ответ:
. Ответ: ![]()
4)6х2 = 0 - уравнение вида ах2 = 0.
6х2 = 0,
х2 = 0,
х = 0. Ответ: 0
1) 5х2 - 5 = 0;
2) 3х2 + 6х = 0;
3) 5х2 + 20 = 0;
4) 4х2 = 0;
5) 5(х - 2)2 - 45 = 0
Карточка 9 Решение неполных квадратных уравнений
Правила
Образцы
Задания ( Вариант 3)
Уравнение вида ах2 = 0
решается так:
ах2 = 0
х2 = 0(а ≠ 0)
х = 0.
Уравнение вида ах2+ bх = 0
решается так:
ах2+ bх = 0
х(ах + b) = 0
x = 0 или ax + b = 0
x = 0 или x = ![]() .
.
Уравнение вида ах2+ c = 0
решается так:
ах2+ c = 0, ax2 = -c,
![]() , где а ≠ 0;
, где а ≠ 0;
1)если ![]() , то корней нет;
, то корней нет;
2)если ![]() ,то х = 0;
,то х = 0;
3) если ![]() , то х =
, то х = ![]() .
.
Решить уравнения:
1) 2х2 + 8 = 0 - уравнение вида ах2+с=0;
2х2 = - 8,
х2 = -4. Ответ: корней нет
2) 3х2 - 2х = 0 - уравнение вида ах2+ bx =0.
3х2 - 2х = 0,
x(3x - 2) = 0,
x = 0 или 3x - 2 = 0,
x = 0 или ![]() . Ответ: 0;
. Ответ: 0; ![]()
3)7х2 - 8 = 0 - уравнение вида ах2 + с = 0.
7х2 - 8 = 0,
7х2 = 8,
х2 = ![]() ,
,
![]() . Ответ:
. Ответ: ![]()
4)6х2 = 0 - уравнение вида ах2 = 0.
6х2 = 0,
х2 = 0,
х = 0. Ответ: 0
1) 3х2 + 12 = 0;
2) 2х2 - 6х = 0;
3) 5х2 - 20 = 0;
4) -7х2 = 0;
5) 3(х + 1)2 - 27 = 0
Карточка 10 Решение квадратных уравнений по формуле
Правила
Образцы
Задания ( Вариант 1)
Чтобы решить квадратное уравнение ах2 + bx + c = 0 по формуле нужно:
вычислить его дискриминант
D = b2 - 4ac.
1) Если D< 0, то корней нет; 2) если D = 0, вычислить единственный корень по формуле ![]() ; 3) если D > 0 , вычислить два корня по формуле
; 3) если D > 0 , вычислить два корня по формуле ![]() .
.
Решить уравнения:
1) 8х2 +4х + 3 = 0 ; a = 8, b = 4, c = 3
Находим дискриминант D = b2 - 4ac,
D = 42 - 4·8·3 = 16 - 96 = - 80 <0 - нет корней. Ответ: нет корней.
2) х2 - 6х + 9 = 0 ; a = 1, b = - 6, c = 9
D = b2 - 4ac = (-6)2 - 4·1·9 =36 - 36 = 0
Находим единственный корень по формуле ![]() =
= ![]() .
.
Ответ: 3.
3) 5х2 - 3х - 2 = 0 ; a = 5, b = - 3, c = - 2.
D = b2 - 4ac = (-3)2 - 4·5·(- 2) =9 + 40 =49,
![]() =
= ![]()
![]()
Ответ: -0,4; 1
1) 3х2 + 5х - 8 = 0;
2) х2 + 5х + 10 = 0;
3) 7х2 - 14х + 7 = 0;
4) - х2+ 3х + 4 = 0;
5) 4(х - 1)2 - 16х = 0
Карточка 10 Решение квадратных уравнений по формуле
Правила
Образцы
Задания ( Вариант 2)
Чтобы решить квадратное уравнение ах2 + bx + c = 0 по формуле нужно:
вычислить его дискриминант
D = b2 - 4ac.
1) Если D< 0, то корней нет; 2) если D = 0, вычислить единственный корень по формуле ![]() ; 3) если D > 0 , вычислить два корня по формуле
; 3) если D > 0 , вычислить два корня по формуле ![]() .
.
Решить уравнения:
1) 8х2 +4х + 3 = 0 ; a = 8, b = 4, c = 3
Находим дискриминант D = b2 - 4ac,
D = 42 - 4·8·3 = 16 - 96 = - 80 <0 - нет корней. Ответ: нет корней.
2) х2 - 6х + 9 = 0 ; a = 1, b = - 6, c = 9
D = b2 - 4ac = (-6)2 - 4·1·9 =36 - 36 = 0
Находим единственный корень по формуле ![]() =
= ![]() .
.
Ответ: 3.
3) 5х2 - 3х - 2 = 0 ; a = 5, b = - 3, c = - 2.
D = b2 - 4ac = (-3)2 - 4·5·(- 2) =9 + 40 =49,
![]() =
= ![]()
![]()
Ответ: -0,4; 1
1) 5х2 + х - 6 = 0;
2) 3х2 + 6х + 3 = 0;
3) 4х2 - 11х - 7 = 0;
4) х2+ 4х + 5 = 0;
5) 5(х - 2)2 - 45х = 0
Карточка 10 Решение квадратных уравнений по формуле
Правила
Образцы
Задания ( Вариант 3)
Чтобы решить квадратное уравнение ах2 + bx + c = 0 по формуле нужно:
вычислить его дискриминант
D = b2 - 4ac.
1) Если D< 0, то корней нет; 2) если D = 0, вычислить единственный корень по формуле ![]() ; 3) если D > 0 , вычислить два корня по формуле
; 3) если D > 0 , вычислить два корня по формуле ![]() .
.
Решить уравнения:
1) 8х2 +4х + 3 = 0 ; a = 8, b = 4, c = 3
Находим дискриминант D = b2 - 4ac,
D = 42 - 4·8·3 = 16 - 96 = - 80 <0 - нет корней. Ответ: нет корней.
2) х2 - 6х + 9 = 0 ; a = 1, b = - 6, c = 9
D = b2 - 4ac = (-6)2 - 4·1·9 =36 - 36 = 0
Находим единственный корень по формуле ![]() =
= ![]() .
.
Ответ: 3.
3) 5х2 - 3х - 2 = 0 ; a = 5, b = - 3, c = - 2.
D = b2 - 4ac = (-3)2 - 4·5·(- 2) =9 + 40 =49,
![]() =
= ![]()
![]()
Ответ: -0,4; 1
1) 2х2 + 7х - 9 = 0;
2) 2 х2 - 4х + 2 = 0;
3) х2 - 10х + 30 = 0;
4) х2+ 5х + 6 = 0;
5) 3(х + 1)2 - 27х = 0
Карточка 11 Решение числовых неравенств
Правила
Образцы
Задания ( Вариант 1)
При решении числовых неравенств можно:
1) переносить слагаемые из одной части неравенства в другую, изменив знаки этих слагаемых на противоположные;
2) делить обе части неравенства на одно и то же положительное число, сохраняя знак неравенства;
3) ) делить обе части неравенства на одно и то же положительное число, сохраняя знак неравенства
Решить неравенство:
-2(х - 3) > 3(x + 5).
Решение:
Раскроем скобки, умножив числа перед скобками на каждое слагаемое в скобках: -2х + 6 > 3x + 15.
Перенесём слагаемые с неизвестным влево, а без неизвестных вправо, изменяя их знаки: -2х - 3х > 15 - 6.
Приведём подобные слагаемые:
-5х > 9, разделим обе части неравенства на отрицательное число - 5, меняя знак неравенства: х< -1,8.
Ответ: ![]()
1) х + 1 < 7;
2) 3 - x < 6 ;
3) 2x - 7 > x;
4) 6 - x < 8 + x;
5) 2(x - 4) > 5 - 7x
Карточка 11 Решение числовых неравенств
Правила
Образцы
Задания ( Вариант 2)
При решении числовых неравенств можно:
1) переносить слагаемые из одной части неравенства в другую, изменив знаки этих слагаемых на противоположные;
2) делить обе части неравенства на одно и то же положительное число, сохраняя знак неравенства;
3) ) делить обе части неравенства на одно и то же положительное число, сохраняя знак неравенства
Решить неравенство:
-2(х - 3) > 3(x + 5).
Решение:
Раскроем скобки, умножив числа перед скобками на каждое слагаемое в скобках: -2х + 6 > 3x + 15.
Перенесём слагаемые с неизвестным влево, а без неизвестных вправо, изменяя их знаки: -2х - 3х > 15 - 6.
Приведём подобные слагаемые:
-5х > 9, разделим обе части неравенства на отрицательное число - 5, меняя знак неравенства: х< -1,8.
Ответ: ![]()
1) х + 2 > 6;
2) 2 - x < 7 ;
3) 3x - 2 > 2x;
4) 2 - x < 7 + x;
5) -(x + 3) > 4 - 6x
Карточка 11 Решение числовых неравенств
Правила
Образцы
Задания ( Вариант 3)
При решении числовых неравенств можно:
1) переносить слагаемые из одной части неравенства в другую, изменив знаки этих слагаемых на противоположные;
2) делить обе части неравенства на одно и то же положительное число, сохраняя знак неравенства;
3) ) делить обе части неравенства на одно и то же положительное число, сохраняя знак неравенства
Решить неравенство:
-2(х - 3) > 3(x + 5).
Решение:
Раскроем скобки, умножив числа перед скобками на каждое слагаемое в скобках: -2х + 6 > 3x + 15.
Перенесём слагаемые с неизвестным влево, а без неизвестных вправо, изменяя их знаки: -2х - 3х > 15 - 6.
Приведём подобные слагаемые:
-5х > 9, разделим обе части неравенства на отрицательное число - 5, меняя знак неравенства: х< -1,8.
Ответ: ![]()
1) х - 4 > 8;
2) 5 + x < 9 ;
3) -x + 3 > x;
4) 4 + x < 4 + 2x;
5) -3(x + 1) < 4 - 7x
9 класс
Карточка № 1. Разложение квадратного трёхчлена на множители / ВАРИАНТ 1 /
ПРАВИЛО
ОБРАЗЦЫ
ЗАДАНИЯ
1. Если у квадратного уравнения ax2 + bx + c = 0 есть корни х1 и х2, то квадратный трёхчлен ax2 + bx + c можно разложить на множители: ax2 + bx + c = a(x - x1)(x - x2).
2. Если у квадратного уравнения ax2 + bx + c = 0 нет корней, то квадратный трёхчлен ax2 + bx + c нельзя разложить на множители.
3. Если у квадратного уравнения ax2 + bx + c = 0 есть один корень х1, то квадратный трёхчлен ax2 + bx + c можно разложить на множители:
ax2 + bx + c = a(x - x1)2.
Следующие квадратные трёхчлены разложить на множители, если это возможно:
1) 2х2 - 5х + 2, 2) 9х2 + 6х + 1, 3) х2 - 2х + 3.
Решение: 1) Рассмотрим уравнение 2х2 - 5х + 2 = 0, D = b2 - 4ac = (-5)2 - 4∙2∙2 =
= 25 - 16 = 9 > 0, ![]()
![]() x2 = 2. Значит,
x2 = 2. Значит,
2х2 - 5х + 2 = ![]()
2) 9х2 + 6х + 1 = 0, D = 62 - 4 ∙ 9 = 0, ![]() .
.
9х2 + 6х + 1 = ![]() .
.
3) х2 - 2х + 3 = 0,D = (-2)2 - 4∙3 = 4 - 12 = - 8 < 0 - нет корней. Значит, трёхчлен х2 - 2х + 3 нельзя разложить на множители.
Разложить на множители, если это возможно:
1) 3х2 + 5х - 8,
2) х2 + 5х + 10,
3)7х2 - 14х + 7,
4) - х2 + 3х + 4,
5) 4(х - 1)2 - 16х.
Карточка № 2. Построение графика квадратичной функции / ВАРИАНТ 1 /
ПРАВИЛО
ОБРАЗЦЫ
ЗАДАНИЯ
Построить параболу у = ах2 + bx + c можно так:
1) найти абсциссу вершины параболы по формуле ![]() ;
;
2) найти ординату вершины параболы по формуле ![]() или по формуле у0 = ах02 + bx0 + c ;
или по формуле у0 = ах02 + bx0 + c ;
3) в координатной плоскости построить точку (х0;у0) - вершину параболы;
4) найти координаты ещё нескольких точек, принадлежащих параболе слева или справа от вершины и отметить их в координатной плоскости и симметричные точки относительно оси параболы ( прямая х = х0).
Построить график функции
у = -0,5х2 + х - 4.
1) ![]()
2) у0 = -0,5∙ 12 + 1 - 4 = -3,5;
3)
х0
0
-1
-2
у0
-4
-5,5
-8
4) ось параболы х = 1; симметричные точки (2;4), (3;-5,5), (4;-8).
5) отмечаем в координатной плоскости вершину параболы и эти точки, затем соединяя их плавной линией.
Построить графики:
1) у = х2 + 5х - 6,
2) у = х2 + 5х,
3) у = -х2 + 7,
4) у = х2 + 2х + 1,
5) у = х2 + х + 1.
Карточка № 3. Решение систем уравнений / ВАРИАНТ 1 /
ПРАВИЛО
ОБРАЗЦЫ
ЗАДАНИЯ
Если одно из уравнений в системе стоит в первой степени, то можно решить эту систему способом подстановки, выразив из этого уравнения какое - либо неизвестное и подставив во второе уравнение полученное выражение и продолжая далее решение.
Решить систему: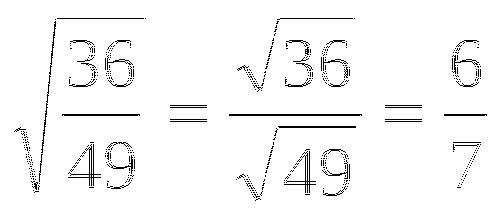
Решение: Уравнение х + у = 7 первой степени (линейное). Поэтому х = 7 - у.
Подставляем это выражение в первое уравнение вместо х: (7 - у)2 + у2 = 25,
49 - 14у + у2 + у2 = 25, 2у2 - 14у + 24 = 0,
у2 - 7у + 12 = 0; у1 = 3, у2 = 4. Подставляем у1 и у2 в уравнение х = 7 - у: х1 = 7 - 3 = 4, х2 = 7 - 4 = 3.
Ответ: (4;3), (3;4).
Решить системы:
1) 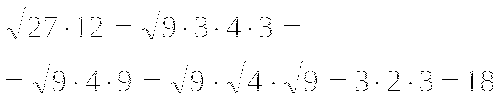
2) 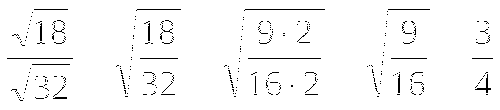
3) 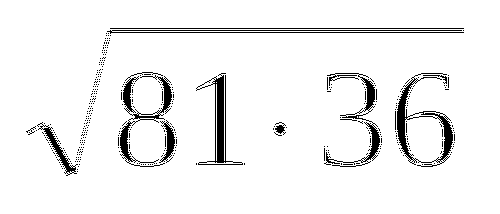
4) 
5) 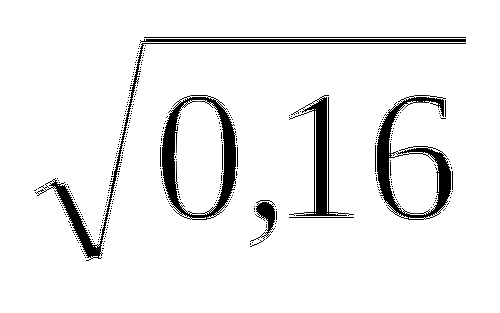
Карточка № 4. Арифметическая прогрессия / ВАРИАНТ 1 /
ПРАВИЛО
ОБРАЗЦЫ
ЗАДАНИЯ
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом:
a п +1 = ап + d.
Формула п-го члена арифметической прогрессии: ап = а1 + d(n - 1).
Заполнить таблицу
n
а1
ап
ап+1
d
1)
5
-2
3
2)
7
21
2
3)
-
-
11
9
Решение: 1) ап = а1 + d(n - 1), а5 = -2 + 3∙4 =10; a п +1 = ап + d, а6 = а5 + d = 10 + 3 = 13.
2) ап = а1 + d(n - 1), 21 = 7 + 2(n - 1),
21 =7 + 2n - 2, 2n = 21 - 7 + 5 = 16, n = 8, a9 = 21 + 2 = 23.
3) a п +1 = ап + d, 9 = 11 + d, d = 9 - 11, d = -2.
Ответы:
n
а1
ап
ап+1
d
1)
5
-2
10
13
3
2)
8
7
21
23
2
3)
-
-
11
9
-2
Заполнить таблицу
n
а1
ап
ап+1
d
1)
-
-
-2
1
2)
-
-
6
4
3)
4
5
1
4)
7
-1
-2
5)
7
-1
-2
Карточка № 5. Сумма членов арифметической прогрессии / ВАРИАНТ 1/
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
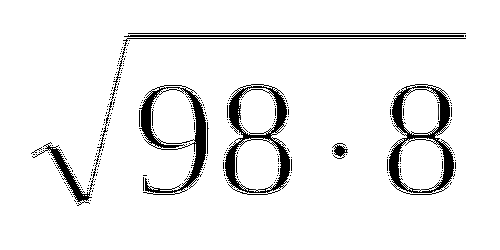
Заполнить таблицу
n
а1
ап
d
Sn
1)
4
7
21
-
2)
5
-2
-
3
Решение: 1)![]()
![]()
2)![]()
![]()
Ответы:
n
а1
ап
d
Sn
1)
4
7
21
-
56
2)
5
-2
-
3
20
Заполнить таблицу
n
а1
ап
d
Sn
1)
5
-2
6
-
1
2)
7
21
2
3)
8
11
9
4)
5
-2
3
5)
7
21
2
Карточка № 6. Геометрическая прогрессия / ВАРИАНТ 1/
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число:
bn+ 1 = bn∙ q.
Формула п-го члена геометрической прогрессии:bn = b1∙qn-1.
Заполнить таблицу
n
b1
bn
bn+1
q
1)
5
-2
3
2)
7
56
2
3)
-
-
-18
9
Решение: 1) bn = b1∙qn-1, b5 = -2∙34 = =-2∙81 = -162; bn+ 1 = bn∙ q, b6 = b5∙q = = -162∙ 3 = -486.
2) bn = b1∙qn-1, 56 = 7 ∙ 2n -1 , 2n -1=56 : 7= = 8 =23, n - 1 = 3, n = 4; b5 = 56 ∙ 2 = =112.
3) bn+ 1 = bn∙ q, 9 = -18 q, q =- 0,5.
Ответы:
n
b1
bn
bn+1
q
1)
5
-2
-162
-486
3
2)
4
7
56
112
2
3)
-
-
-18
9
-0,5
Заполнить таблицу
n
b1
bп
bn+1
d
1)
-
-
-2
1
2)
-
-
6
4
3)
4
5
1
4)
7
-1
-2
5)
7
-1
- 2
Карточка № 7. Сумма членов геометрической прогрессии / ВАРИАНТ 1/
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
Если q ≠ 1, то сумму п первых членов геометрической прогрессии можно найти по формулам:
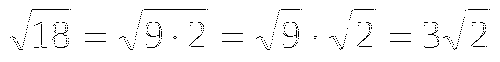 .
.
Если q = 1, то Sn = b1n.
Найти сумму первых четырёх членов геометрической прогрессии, у которой первый член равен 7, а четвёртый равен -56.
Решение: ![]()
![]()
Найдём q: b4 = -56; b1q3 = -56 ; 7q3 = -56;
q3 = -8; q = -2.
![]()
Заполнить таблицу
n
b1
bп
q
Sn
1)
4
1
-8
-
2)
64
1
4
85
3)
5
2
-
3
4)
4
0,1
0,1
5)
10
7
7
Карточка № 8. Сумма членов геометрической прогрессии / ВАРИАНТ 1/
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
Геометрическая прогрессия называется бесконечно убывающей, если ![]() У неё ( при бесконечном увеличении числа членов)
У неё ( при бесконечном увеличении числа членов) ![]() , называемому суммой прогрессии и вычисляется по формуле:
, называемому суммой прогрессии и вычисляется по формуле: ![]()
Найти первый член бесконечно убывающей геометрической прогрессии, знаменатель которой равен -0,1, а сумма S равна 6.
Решение: ![]()
![]()
b1= 6,6.
Заполнить таблицу
b1
q
S
1)
5
0,2
2)
3
21
3)
0,5
11
4)
5
-0,2
5)
-3
21
Карточка № 1. Разложение квадратного трёхчлена на множители / ВАРИАНТ 2 /
ПРАВИЛО
ОБРАЗЦЫ
ЗАДАНИЯ
1. Если у квадратного уравнения ax2 + bx + c = 0 есть корни х1 и х2, то квадратный трёхчлен ax2 + bx + c можно разложить на множители: ax2 + bx + c = a(x - x1)(x - x2).
2. Если у квадратного уравнения ax2 + bx + c = 0 нет корней, то квадратный трёхчлен ax2 + bx + c нельзя разложить на множители.
3. Если у квадратного уравнения ax2 + bx + c = 0 есть один корень х1, то квадратный трёхчлен ax2 + bx + c можно разложить на множители:
ax2 + bx + c = a(x - x1)2.
Следующие квадратные трёхчлены разложить на множители, если это возможно:
1) 2х2 - 5х + 2, 2) 9х2 + 6х + 1, 3) х2 - 2х + 3.
Решение: 1) Рассмотрим уравнение 2х2 - 5х + 2 = 0, D = b2 - 4ac = (-5)2 - 4∙2∙2 =
= 25 - 16 = 9 > 0, ![]()
![]() x2 = 2. Значит,
x2 = 2. Значит,
2х2 - 5х + 2 = ![]()
2) 9х2 + 6х + 1 = 0, D = 62 - 4 ∙ 9 = 0, ![]() .
.
9х2 + 6х + 1 = ![]() .
.
3) х2 - 2х + 3 = 0,D = (-2)2 - 4∙3 = 4 - 12 = - 8 < 0 - нет корней. Значит, трёхчлен х2 - 2х + 3 нельзя разложить на множители.
Разложить на множители, если это возможно:
1) 5х2 + х - 6,
2) 3х2 + 6х + 3,
3) х2 + 4х + 5,
4) 4х2 - 11х - 7,
5) 5(х - 2)2 - 45х.
Карточка № 2. Построение графика квадратичной функции / ВАРИАНТ 2 /
ПРАВИЛО
ОБРАЗЦЫ
ЗАДАНИЯ
Построить параболу у = ах2 + bx + c можно так:
1) найти абсциссу вершины параболы по формуле ![]() ;
;
2) найти ординату вершины параболы по формуле ![]() или по формуле у0 = ах02 + bx0 + c ;
или по формуле у0 = ах02 + bx0 + c ;
3) в координатной плоскости построить точку (х0;у0) - вершину параболы;
4) найти координаты ещё нескольких точек, принадлежащих параболе слева или справа от вершины и отметить их в координатной плоскости и симметричные точки относительно оси параболы ( прямая х = х0).
Построить график функции
у = -0,5х2 + х - 4.
1) ![]()
2) у0 = -0,5∙ 12 + 1 - 4 = -3,5;
3)
х0
0
-1
-2
у0
-4
-5,5
-8
4) ось параболы х = 1; симметричные точки (2;4), (3;-5,5), (4;-8).
5) отмечаем в координатной плоскости вершину параболы и эти точки, затем соединяя их плавной линией.
Построить графики:
1) у = х2 - х - 6,
2) у = 3х2 + 6х,
3) у = -х2 + 5,
4) у = 0,5х2 + х + 0,5,
5) у = х2 - х + 1.
Карточка № 3. Решение систем уравнений / ВАРИАНТ 2 /
ПРАВИЛО
ОБРАЗЦЫ
ЗАДАНИЯ
Если одно из уравнений в системе стоит в первой степени, то можно решить эту систему способом подстановки, выразив из этого уравнения какое - либо неизвестное и подставив во второе уравнение полученное выражение и продолжая далее решение.
Решить систему: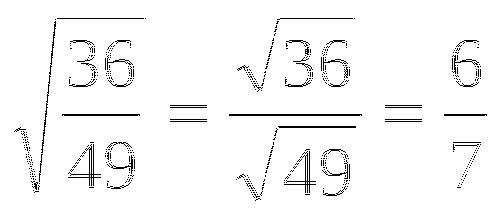
Решение: Уравнение х + у = 7 первой степени (линейное). Поэтому х = 7 - у.
Подставляем это выражение в первое уравнение вместо х: (7 - у)2 + у2 = 25,
49 - 14у + у2 + у2 = 25, 2у2 - 14у + 24 = 0,
у2 - 7у + 12 = 0; у1 = 3, у2 = 4. Подставляем у1 и у2 в уравнение х = 7 - у: х1 = 7 - 3 = 4, х2 = 7 - 4 = 3.
Ответ: (4;3), (3;4).
Решить системы:
1) 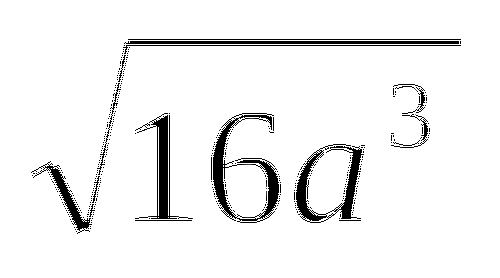
2) 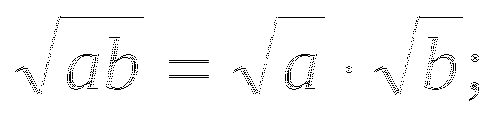
3) 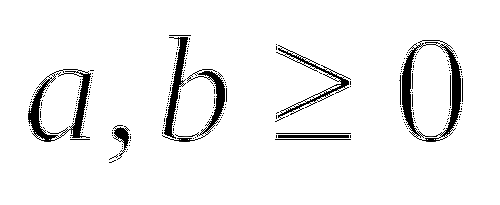
4) 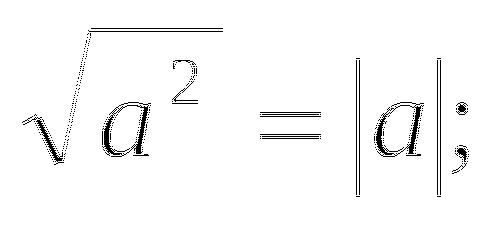
5) 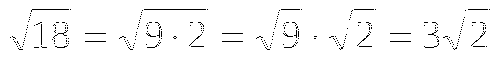 .
.
Карточка № 4. Арифметическая прогрессия / ВАРИАНТ 2 /
ПРАВИЛО
ОБРАЗЦЫ
ЗАДАНИЯ
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом:
a п +1 = ап + d.
Формула п-го члена арифметической прогрессии: ап = а1 + d(n - 1).
Заполнить таблицу
n
а1
ап
ап+1
d
1)
5
-2
3
2)
7
21
2
3)
-
-
11
9
Решение: 1) ап = а1 + d(n - 1), а5 = -2 + 3∙4 =10; a п +1 = ап + d, а6 = а5 + d = 10 + 3 = 13.
2) ап = а1 + d(n - 1), 21 = 7 + 2(n - 1),
21 =7 + 2n - 2, 2n = 21 - 7 + 5 = 16, n = 8, a9 = 21 + 2 = 23.
3) a п +1 = ап + d, 9 = 11 + d, d = 9 - 11, d = -2.
Ответы:
n
а1
ап
ап+1
d
1)
5
-2
10
13
3
2)
8
7
21
23
2
3)
-
-
11
9
-2
Заполнить таблицу
n
а1
ап
ап+1
d
1)
-
-
8
3
2)
-
-
5
2
3)
5
4
2
4)
6
17
-3
5)
4
9
10
Карточка № 5. Сумма членов арифметической прогрессии / ВАРИАНТ 2/
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
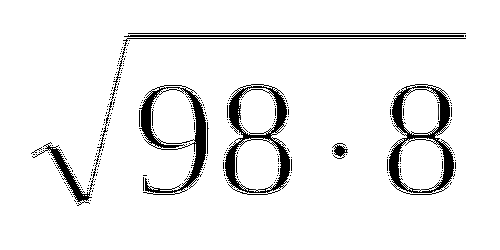
Заполнить таблицу
n
а1
ап
d
Sn
1)
4
7
21
-
2)
5
-2
-
3
Решение: 1)![]()
![]()
2)![]()
![]()
Ответы:
n
а1
ап
d
Sn
1)
4
7
21
-
56
2)
5
-2
-
3
20
Заполнить таблицу
n
а1
ап
d
Sn
1)
4
-4
0
2)
4
2
11
-
3)
5
-22
-10
4)
4
0
24
5)
3
-13
-
Карточка № 6. Геометрическая прогрессия / ВАРИАНТ 2/
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число:
bn+ 1 = bn∙ q.
Формула п-го члена геометрической прогрессии:bn = b1∙qn-1.
Заполнить таблицу
n
b1
bn
bn+1
q
1)
5
-2
3
2)
7
56
2
3)
-
-
-18
9
Решение: 1) bn = b1∙qn-1, b5 = -2∙34 = =-2∙81 = -162; bn+ 1 = bn∙ q, b6 = b5∙q = = -162∙ 3 = -486.
2) bn = b1∙qn-1, 56 = 7 ∙ 2n -1 , 2n -1=56 : 7 = 8 =23, n - 1 = 3, n = 4; b5 = 56 ∙ 2 = 112.
3) bn+ 1 = bn∙ q, 9 = -18 q, q =- 0,5.
Ответы:
n
b1
bn
bn+1
q
1)
5
-2
-162
-486
3
2)
4
7
56
112
2
3)
-
-
-18
9
-0,5
Заполнить таблицу
n
b1
bп
bn+1
d
1)
-
-
8
3
2)
-
-
5
2
3)
5
4
2
4)
6
17
-3
5)
4
9
10
Карточка № 7. Сумма членов геометрической прогрессии / ВАРИАНТ 2/
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
Если q ≠ 1, то сумму п первых членов геометрической прогрессии можно найти по формулам:
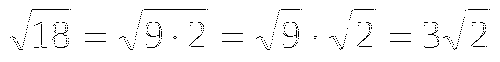 .
.
Если q = 1, то Sn = b1n.
Найти сумму первых четырёх членов геометрической прогрессии, у которой первый член равен 7, а четвёртый равен -56.
Решение: ![]()
![]()
Найдём q: b4 = -56; b1q3 = -56 ; 7q3 = -56;
q3 = -8; q = -2.
![]()
Заполнить таблицу
n
b1
bп
q
Sn
1)
5
16
1
-
2)
1
16
0,25
21
3)
4
-1
-
-2
4)
5
10
10
5)
4
-2
-2
Карточка № 8. Сумма членов геометрической прогрессии / ВАРИАНТ 2/
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
Геометрическая прогрессия называется бесконечно убывающей, если ![]() У неё ( при бесконечном увеличении числа членов)
У неё ( при бесконечном увеличении числа членов) ![]() , называемому суммой прогрессии и вычисляется по формуле:
, называемому суммой прогрессии и вычисляется по формуле: ![]()
Найти первый член бесконечно убывающей геометрической прогрессии, знаменатель которой равен -0,1, а сумма S равна 6.
Решение: ![]()
![]()
b1= 6,6.
Заполнить таблицу
b1
q
S
1)
8
0,01
2)
4
16
3)
7
21
4)
4
-0,8
5)
5
-7
Карточка № 1. Разложение квадратного трёхчлена на множители / ВАРИАНТ 3 /
ПРАВИЛО
ОБРАЗЦЫ
ЗАДАНИЯ
1. Если у квадратного уравнения ax2 + bx + c = 0 есть корни х1 и х2, то квадратный трёхчлен ax2 + bx + c можно разложить на множители: ax2 + bx + c = a(x - x1)(x - x2).
2. Если у квадратного уравнения ax2 + bx + c = 0 нет корней, то квадратный трёхчлен ax2 + bx + c нельзя разложить на множители.
3. Если у квадратного уравнения ax2 + bx + c = 0 есть один корень х1, то квадратный трёхчлен ax2 + bx + c можно разложить на множители:
ax2 + bx + c = a(x - x1)2.
Следующие квадратные трёхчлены разложить на множители, если это возможно:
1) 2х2 - 5х + 2, 2) 9х2 + 6х + 1, 3) х2 - 2х + 3.
Решение: 1) Рассмотрим уравнение 2х2 - 5х + 2 = 0, D = b2 - 4ac = (-5)2 - 4∙2∙2 =
= 25 - 16 = 9 > 0, ![]()
![]() x2 = 2. Значит,
x2 = 2. Значит,
2х2 - 5х + 2 = ![]()
2) 9х2 + 6х + 1 = 0, D = 62 - 4 ∙ 9 = 0, ![]() .
.
9х2 + 6х + 1 = ![]() .
.
3) х2 - 2х + 3 = 0,D = (-2)2 - 4∙3 = 4 - 12 = - 8 < 0 - нет корней. Значит, трёхчлен х2 - 2х + 3 нельзя разложить на множители.
Разложить на множители, если это возможно:
1) 2х2 + 7х - 9,
2) 2х2 - 4х + 2,
3) х2 - 10х + 30,
4) х2 + 5х + 6,
5) 3(х + 1)2 - 27х.
Карточка № 2. Построение графика квадратичной функции / ВАРИАНТ 3 /
ПРАВИЛО
ОБРАЗЦЫ
ЗАДАНИЯ
Построить параболу у = ах2 + bx + c можно так:
1) найти абсциссу вершины параболы по формуле ![]() ;
;
2) найти ординату вершины параболы по формуле ![]() или по формуле у0 = ах02 + bx0 + c ;
или по формуле у0 = ах02 + bx0 + c ;
3) в координатной плоскости построить точку (х0;у0) - вершину параболы;
4) найти координаты ещё нескольких точек, принадлежащих параболе слева или справа от вершины и отметить их в координатной плоскости и симметричные точки относительно оси параболы ( прямая х = х0).
Построить график функции
у = -0,5х2 + х - 4.
1) ![]()
2) у0 = -0,5∙ 12 + 1 - 4 = -3,5;
3)
х0
0
-1
-2
у0
-4
-5,5
-8
4) ось параболы х = 1; симметричные точки (2;4), (3;-5,5), (4;-8).
5) отмечаем в координатной плоскости вершину параболы и эти точки, затем соединяя их плавной линией.
Построить графики:
1) у = х2 + 6х + 8,
2) у = 2х2 - 4х + 2,
3) у = х2 - 3х,
4) у = -х2 + 4х - 4,
5) у = х2 - 2х + 2.
Карточка № 3. Решение систем уравнений / ВАРИАНТ 3 /
ПРАВИЛО
ОБРАЗЦЫ
ЗАДАНИЯ
Если одно из уравнений в системе стоит в первой степени, то можно решить эту систему способом подстановки, выразив из этого уравнения какое - либо неизвестное и подставив во второе уравнение полученное выражение и продолжая далее решение.
Решить систему: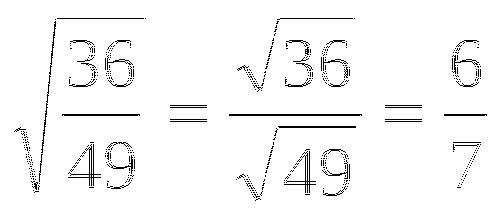
Решение: Уравнение х + у = 7 первой степени (линейное). Поэтому х = 7 - у.
Подставляем это выражение в первое уравнение вместо х: (7 - у)2 + у2 = 25,
49 - 14у + у2 + у2 = 25, 2у2 - 14у + 24 = 0,
у2 - 7у + 12 = 0; у1 = 3, у2 = 4. Подставляем у1 и у2 в уравнение х = 7 - у: х1 = 7 - 3 = 4, х2 = 7 - 4 = 3.
Ответ: (4;3), (3;4).
Решить системы:
1) 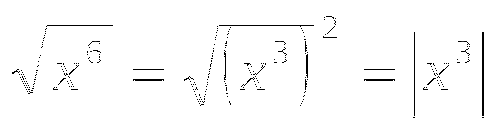
2) 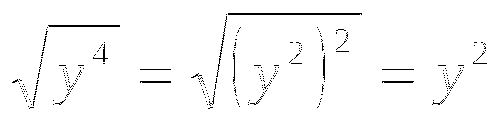
3) 
4) 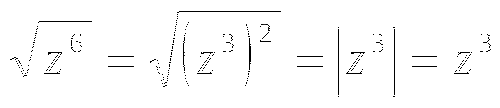
5) 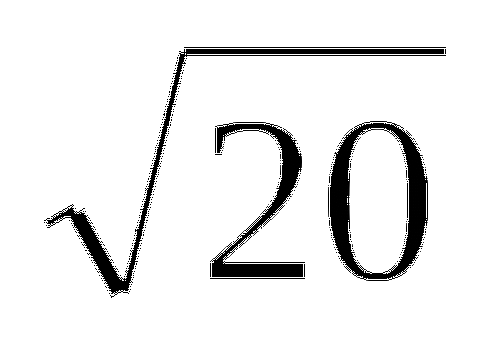
Карточка № 4. Арифметическая прогрессия / ВАРИАНТ 3 /
ПРАВИЛО
ОБРАЗЦЫ
ЗАДАНИЯ
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом:
a п +1 = ап + d.
Формула п-го члена арифметической прогрессии: ап = а1 + d(n - 1).
Заполнить таблицу
n
а1
ап
ап+1
d
1)
5
-2
3
2)
7
21
2
3)
-
-
11
9
Решение: 1) ап = а1 + d(n - 1), а5 = -2 + 3∙4 =10; a п +1 = ап + d, а6 = а5 + d = 10 + 3 = 13.
2) ап = а1 + d(n - 1), 21 = 7 + 2(n - 1),
21 =7 + 2n - 2, 2n = 21 - 7 + 5 = 16, n = 8, a9 = 21 + 2 = 23.
3) a п +1 = ап + d, 9 = 11 + d, d = 9 - 11, d = -2.
Ответы:
n
а1
ап
ап+1
d
1)
5
-2
10
13
3
2)
8
7
21
23
2
3)
-
-
11
9
-2
Заполнить таблицу
n
а1
ап
ап+1
d
1)
-
-
5
7
2)
-
-
3
3
3)
4
8
-1
4)
5
10
3
5)
8
6
2
Карточка № 5. Сумма членов арифметической прогрессии / ВАРИАНТ 3/
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
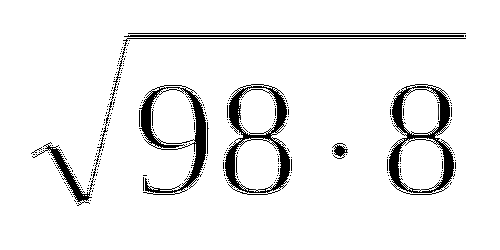
Заполнить таблицу
n
а1
ап
d
Sn
1)
4
7
21
-
2)
5
-2
-
3
Решение: 1)![]()
![]()
2)![]()
![]()
Ответы:
n
а1
ап
d
Sn
1)
4
7
21
-
56
2)
5
-2
-
3
20
Заполнить таблицу
n
а1
ап
d
Sn
1)
5
3
-13
-
1
2)
0
16
40
3)
4
18
10
4)
4
4
-2
0
5)
2
11
26
Карточка № 5. Геометрическая прогрессия / ВАРИАНТ 3/
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число:
bn+ 1 = bn∙ q.
Формула п-го члена геометрической прогрессии:bn = b1∙qn-1.
Заполнить таблицу
n
b1
bn
bn+1
q
1)
5
-2
3
2)
7
56
2
3)
-
-
-18
9
Решение: 1) bn = b1∙qn-1, b5 = -2∙34 = =-2∙81 = -162; bn+ 1 = bn∙ q, b6 = b5∙q = = -162∙ 3 = -486.
2) bn = b1∙qn-1, 56 = 7 ∙ 2n -1 , 2n -1=56 : 7 = 8 =23, n - 1 = 3, n = 4; b5 = 56 ∙ 2 = 112.
3) bn+ 1 = bn∙ q, 9 = -18 q, q =- 0,5.
Ответы:
n
b1
bn
bn+1
q
1)
5
-2
-162
-486
3
2)
4
7
56
112
2
3)
-
-
-18
9
-0,5
Заполнить таблицу
n
b1
bп
bn+1
d
1)
-
-
5
7
2)
-
-
3
3
3)
4
8
-1
4)
5
10
3
5)
8
6
2
Карточка № 7. Сумма членов геометрической прогрессии / ВАРИАНТ 3/
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
Если q ≠ 1, то сумму п первых членов геометрической прогрессии можно найти по формулам:
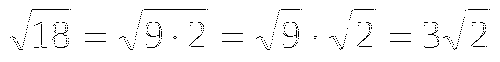 .
.
Если q = 1, то Sn = b1n.
Найти сумму первых четырёх членов геометрической прогрессии, у которой первый член равен 7, а четвёртый равен -56.
Решение: ![]()
![]()
Найдём q: b4 = -56; b1q3 = -56 ; 7q3 = -56;
q3 = -8; q = -2.
![]()
Заполнить таблицу
n
b1
bп
q
Sn
1)
6
2
486
2)
64
-1
4
51
3)
5
-2
-
-1
4)
4
-8
-2
5)
100
11
11
Карточка № 8. Сумма членов геометрической прогрессии / ВАРИАНТ 3/
ФОРМУЛЫ
ОБРАЗЦЫ
ЗАДАНИЯ
Геометрическая прогрессия называется бесконечно убывающей, если ![]() У неё ( при бесконечном увеличении числа членов)
У неё ( при бесконечном увеличении числа членов) ![]() , называемому суммой прогрессии и вычисляется по формуле:
, называемому суммой прогрессии и вычисляется по формуле: ![]()
Найти первый член бесконечно убывающей геометрической прогрессии, знаменатель которой равен -0,1, а сумма S равна 6.
Решение: ![]()
![]()
b1= 6,6.
Заполнить таблицу
b1
q
S
1)
7
0,5
2)
8
11
3)
3
3
4)
6
-0,7
5)
-8
11