Метод интервалов (методические рекомендации)8-11 классы

</ Метод интервалов

(методические рекомендации)

Одним из методов решения неравенств (рациональных, иррациональных и др. ) является метод интервалов, применение которого формируется в 8-9 классах, при решении линейных и квадратных неравенств.

Рассматривая более сложные задачи при решении неравенств вида ( один из знаков сравнения: < , , > , ) методом интервалов можно придерживаться, например, такого алгоритма.

Алгоритм решения неравенств методом интервалов

1. Найти область определения функции ( D(f) ).

2. Найти нули функции ( найти корни уравнения ).

3. Разбить область определения нулями функции на интервалы

(учитывая «строгий» или «нестрогий» знак исходного неравенства, нули функции на оси Ох соответственно «выкалываются» или «не выкалываются»).

4. Определить знак внутри каждого из полученных интервалов методом пробной точки (при этом возможно применение «правила чередования» знаков).

5. Выделить те числовые промежутки, на которых функция принимает соответствующий данному неравенству знак (если знак неравенства «нестрогий», то включить и не выколотые точки - нули функции).

6. Записать ответ.

Замечание. На практике пункты 3-5 можно объединить.

Примеры.

№1. Решите неравенство .

Решение.

Рассмотрим функцию .

1) D(f) = R .

2) Нули функции:

или

нет корней

3) , ,

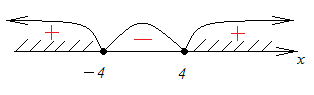
Ответ: .

Замечание. Способы решения неравенства могут быть и другими, например: , где верно при любых действительных значениях x.

Исходное неравенство равносильно неравенству

Ответ: .

№2. Решите неравенство .

Решение.

Рассмотрим функцию .

1) D(f) = R .

2) Нули функции:

или

3) , , ,

Ответ: .

Замечание. Способ решения неравенства может быть и другим:

Применяем метод интервалов, используя сокращенный вариант оформления

Ответ: .

№3. Решите неравенство .

Решение.

Рассмотрим функцию .

1) D(f):

2) Нули функции:

3) ,

Ответ: .

Замечание 1. Способ решения неравенства может быть и другим:

1) ОДЗ:

2) Проверим крайнюю точку ОДЗ: решение неравенства (проверка).

3) Если , то .

Учитывая это условие, решим систему:

,

.

4) Объединяем полученные результаты:

.

Ответ: .

Замечание 2. При решении нестрогих неравенств вида

можно воспользоваться переходом к соответствующей совокупности:

или .

Такой переход можно обобщить и для неравенств , заменяя их совокупностью: или

Замечание 3. Стоит обратить внимание обучающихся и на частые рассуждения, приводящие к потере решений:

т.к. , то , тогда , получаем.

Произошла потеря решения .

Вывод. Демонстрация решений задач различными способами, в том числе и ошибочными, достаточно хороший метод обучения, дающий возможность обучающимся делать выбор наиболее приемлемого для себя способа решения той или иной задачи.

№4. Найдите область определения функции

Решение. (Используем метод интервалов)

Для нахождения D(у) достаточно решить неравенство .

Рассмотрим функцию .

1) D(f) : , ,

2) Нули функции:

3) ,

Ответ: .

Замечание. Переход к системе ведет к потере решения

№5. Решите неравенство .

Решение.

Рассмотрим функцию .

1) D(f):

2) Нули функции:

(В ходе решения уравнения могут появиться посторонние корни )

3)

Проверка: ; ,

следовательно: - не являются решением неравенства.

Вывод. - решение неравенства

Ответ: .

№6. Решите неравенство .

Способ 1.

Решение.

Рассмотрим функцию .

1) D(f):

2) Нули функции:

(посторонний корень уравнения нулем функции не является)

Так как неравенство нестрогое, то нули функции являются решениями исходного неравенства.

3) ;

Вывод. - решение неравенства

Ответ: .

Способ 2*. (используeм вспомогательный тригонометрический аргумент).

.

1) ОДЗ:

2) Пусть , тогда , значит .

Решим неравенство:

Учитывая условие , получим

Для решения неравенства воспользуемся методом интервалов, на промежутке

Нули функции:

Функция - возрастающяя на промежутке , поэтому

Ответ: .

Задача 7*.

alexlarin.net/

вариант 130

задача №15

Решите неравенство

.

Способ 1*. (используем вспомогательный тригонометрический аргумент).

1) ОДЗ:

2) Проверим крайние точки ОДЗ:

а) решение неравенства (проверка);

б) не является решением неравенства (проверка).

3) Рассмотрим остальные значения переменной, входящие в ОДЗ,

.

Пусть , тогда , значит .

Решим неравенство:

, где ,

Для решения неравенства воспользуемся методом интервалов, на промежутке

Нули функции:

Функция - возрастающяя на интервале , поэтому

4) Объединяем полученные результаты:

Ответ: .

Замечание.

При решении этой задачи можно выполнить и другую замену:

1) ОДЗ:

2) Пусть , тогда , значит .

Решим неравенство:

, где ,

(*)

Для решения неравенства (*) воспользуемся методом интервалов, на промежутке

Нули функции:

нули функции являются решением тригонометрического неравенства (*)

Проверим крайние точки:

- не является решением неравенства (*);

- является решением неравенства (*).

Вывод:

Функция - убывающая на отрезке , поэтому

Ответ: .

Турков А.Ф.

Заслуженный учитель РФ, учитель математики МАОУ «Лицей № 38»,

г. Нижний Новгород