Конспект вне классного мероприятия «Чудеса на математических переменках» для 5 - 9 классов

Чудеса на математических переменках

Внеклассное мероприятие для 5 - 9 классов

Предлагаемый материал можно использовать в рамках недели математики или в качестве материала для кружков, внеклассных мероприятий. Математические переменки способствуют развитию личностных качеств обучающихся, активизируют их мыслительную деятельность, поддерживают и развивают пусть и небольшие творческие взлёты.

Учитель математики СКОШИ «Эверест» г. Екатеринбурга

Кочева Елена Владимировна

01. 04. 14.

Одним из путей повышения интереса к предмету является хорошо организованная внеклассная работа - например, проведение предметной недели. Предлагаемый материал можно использовать в рамках недели математики на переменах или в качестве материала для кружков, внеклассных мероприятий. Проведенные математические переменки способствуют развитию личностных качеств обучающихся, активизируют их мыслительную деятельность, поддерживают и развивают пусть и небольшие творческие взлёты. Материал составлен для учащихся 5-9 классов специальной коррекционной школы VI вида, который можно использовать и для учащихся общеобразовательных школ.

Цель: совершенствовать вычислительные навыки учащихся; познакомить учащихся с приемами умножения на 9 разными способами; рассказать и показать другие способы умножения на двузначное и трехзначное число с помощью дополнительных построений (линий, кругов); формирование активного познавательного интереса к предмету средствами увлекательных математических переменок.

Оборудование: таблички с заданиями или задания на слайдах на интерактивной доске, цветной мел, чистые листочки, карандаши.

Ход занятия

Учитель: Я, как главный фокусник и мой помощник, приветствуем вас в студии «Математические чудеса». Мы все изучали таблицу умножения и помним ее. Сегодня мы собрались на переменке, чтобы узнать, как умножали в древности, как с помощью пальцев умножить на 9, рассмотреть необычный способ умножения на 9.

Помощник: А так же познакомимся с быстрым способом умножения двузначных чисел на 11, попытаемся разобраться с необычным способом умножения на двузначное и трехзначное число.

Учитель: И в завершении нашей переменки вы увидите математический фокус. Тот, кто сумеет разгадать секрет этого фокуса, получит приз.

Помощник: А как изучали таблицу умножения в древности?

В римской школе таблицу умножения заучивали только до пяти, а дальше считали на пальцах. Римский писатель Цицерон (1в. до н.э.) считал такой метод преподавания неверным.

Для перемножения чисел А и Б, которые оба больше пяти, но меньше десяти, нужно было вытянуть на одной и другой руке столько пальцев, на сколько единиц данные числа, каждое в отдельности, больше 5.

- Сумма чисел вытянутых пальцев дает разряд десятков произведения.

- К ним надо прибавить произведение чисел, соответствующих оставшимся загнутым пальцам (оба эти числа меньше пяти).

Например: я хочу найти произведение чисел 6 и 8, то на одной руке вытягиваю 1 палец (т.к. 6-5=1), на другой 3 пальца (8-5=3). Сумма чисел 1и 3 равно 4 (3+1=4). Это число десятков. Остались загнутыми 4 и 2 пальца. Нахожу их произведение 42=8. Это число единиц. Получилось 48.

Как интересно! А вы, ребята, так сможете? Давайте попробуем.

Например: 78, 69.

Помощник: Я могу показать вам, как вспомнить умножение на 9, выполняя всего лишь одно действие вычитания. А также рассмотрите, какая получается закономерность в записи чисел ответов при умножении на 9. Посмотрите, что получается:

91 = 10 - 1 = 9 91 = 09

92 = 20 - 2 = 18 92 = 18

93 = 30 - 3 = 27 93 = 27

94 = 40 - 4 = 36 94 = 36

95 = 50 - 5 = 45 95 = 45

96 = 60 - 6 = 54 96 = 54

97 = 70 - 7 = 63 97 = 63

98 = 80 - 8 = 72 98 = 72

99 = 90 - 9 = 81 99 = 81

910 = 100 - 10 = 90 910 = 90

Учитель: Я знаю быстрый способ умножения чисел на 9.

Положите перед собой раскрытые ладони, отсчитывайте слева направо палец с тем номером, который вы хотите умножить на 9. Загните этот палец вниз (поднимите) в зависимости от двигательных возможностей пальцев рук. Тогда число пальцев слева от загнутого (поднятого) - это число десятков в ответе. А число пальцев справа от загнутого (поднятого) - число единиц в нем. Например: 69=54, слева от загнутого - 5 пальцев (десятки произведения), справа от загнутого - 4 пальца (единицы произведения).

Помощник: Я расскажу, как быстро умножить двузначное число на 11. Например: 63 11 = 6 9 3

(6+3=9) или 45 11 = 4 9 5

(4+5=9) или 86 11 = 8(1 4) 6 = 9 4 6

(8+6=14), (8+1=9).

Задание: проверьте, правильно ли выполнено действие, используя способ умножения столбиком.

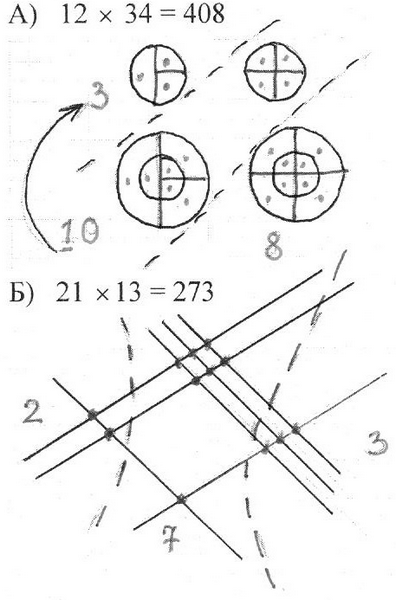
Учитель: Существует необычный способ умножения на двузначные и трехзначные числа. Например: А) 12 умножить на 34 . В первой строке рисуем два круга (12 - 1 десяток - 1 круг), во втором ряду рисуем по два круга: один в другом (12 - 2 единицы - 2 круга). В первом столбике делим круги на 3 части (34 - 3 десятка - 3 части), а во втором столбике делим круги на 4 части (34 - 4 единицы - 4 части). Пунктиром разделяем на три области: 1 круг - первая область, 2 и 3 круги - вторая область и 4 круг - третья область. Получается, что в первой области - 3 части, во второй области - 10 частей, а в третьей области - 8 частей. Следовательно, 3(10) 8 - 3 сотни, 10 десятков, 8 единиц - 4 сотни 0 десятков, 8 единиц. В результате, в числе 3+1=4 сотни, 0 десятков и 8 единиц, т.е. число - 408.

Задание: попробуйте новым способом выполнить умножение чисел 21 и 13 и рассказать все этапы этого способа.

Учитель: Б) Рассмотрим другой способ умножения 21 и 13. Число 21 - рисуем наискосок сначала 2 линии и затем 1 линию. Затем в другую сторону наискосок 1 линию и 3 линии - 13. Разделяем пунктирной линией на три части и считаем, сколько точек получилось при пересечении линий в каждой части. Получилось, что в первой части 2 точки - 2 сотни, во второй 7 точек - 7 десятков, а в третьей 3 точки - 3 единицы. Таким образом, произведение чисел 21 и 13 равно 273.

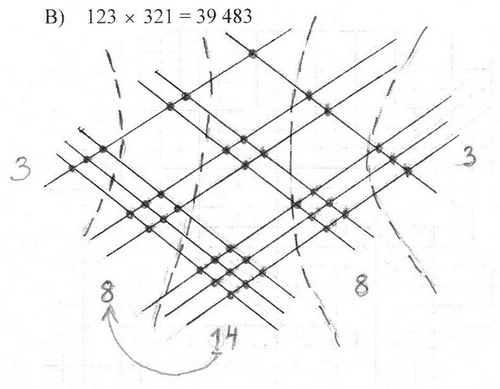
Задание: попробуйте новым способом выполнить умножение чисел 123 и 321. Проверьте, правильно ли выполнено действие, используя способ умножения столбиком.

Помощник: Я хочу показать математический фокус «Предсказывание результата».

А) Первой число я пишу - 159 654. Под ним предлагаю записать любое шестизначное число. Под записанным снова я пишу шестизначное число, затем - предлагаю записать следующее любое шестизначное число и последнее число пишу я. Предлагаю сложить пять шестизначных чисел или столбиком или с помощью калькулятора. Какое число получилось в результате? Я могу заранее сказать, что это число - 2 159 652.

Б) Можно предложить четырехзначное число - 1 528 и выполнить записи чисел по ранее указанному правилу. В результате получится число - 21 526.

В) Другой вариант фокуса - трехзначное число 372 и результат сложения - 2 370.

Г) Для устного счета можно предложить двузначное число - 13 и результат сложения - 211.

6 - учитель

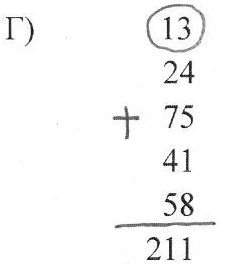
Задание. Попытайтесь объяснить этот математический фокус. Кто угадает в чем секрет этого фокуса, того ждет приз.

До новых встреч на математических переменках!