- Учителю
- Урок алгебры в 8 классе 'Уравнения, сводящиеся к квадратным'
Урок алгебры в 8 классе 'Уравнения, сводящиеся к квадратным'
Тема: «Уравнения, сводящиеся к квадратным»
Цели: Закрепить навыки решения уравнений, сводящихся к квадратным; ликвидировать пробелы в знаниях и умениях учащихся; расширить кругозор учащихся; пополнить их словарный запас; развивать интерес учащихся к предмету и смежным дисциплинам; развивать личностные качества учащихся, их коммуникативные характеристики.
Структура урока:
-
Постановка темы и цели урока.
-
Актуализация опорных знаний учащихся.
-
Работа учащихся над заданиями.
-
Подведение итогов урока.
-
Постановка домашнего задания.
Ход урока:
-
а) приветствие учащихся; проверка их готовности к уроку;
б) сообщение темы урока: заключительный урок по теме: «Уравнения, сводящиеся к квадратным».
в) сообщение целей и задач урока: учащиеся должны показать, как они умеют применять знания, полученные при изучении темы «Уравнения, сводящиеся к квадратным».
-
Устная работа с классом, во время которой 6 учащихся выполняют индивидуальные задания.
а) Решите неполное квадратное уравнение: х2 + 3х = 0; у2 - 121 = 0; 5х2 = 3х; -1/3х2 = 0
б) Не решая уравнение, найдите сумму и произведение его корней: х2 + 17х - 38 = 0;
х2 - 16х + 4 = 0; 3х2 + 8х - 15 = 0
в) Найдите общий знаменатель для дробей:
![]() ;
; ![]() ;
; ![]() ;
; ![]()
г) Решите уравнение:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
д) Составьте задачу по уравнению:
![]()
х(х - 5) = 84
-
Учащиеся выполняют задания по группам. В системе координат отмечают точки, координаты которых совпадают по своим значениям со значениями корней уравнений. В результате такой работы появляется изображение созвездия «Андромеды»
1 группа
Решите уравнения:
-
у - 10 =
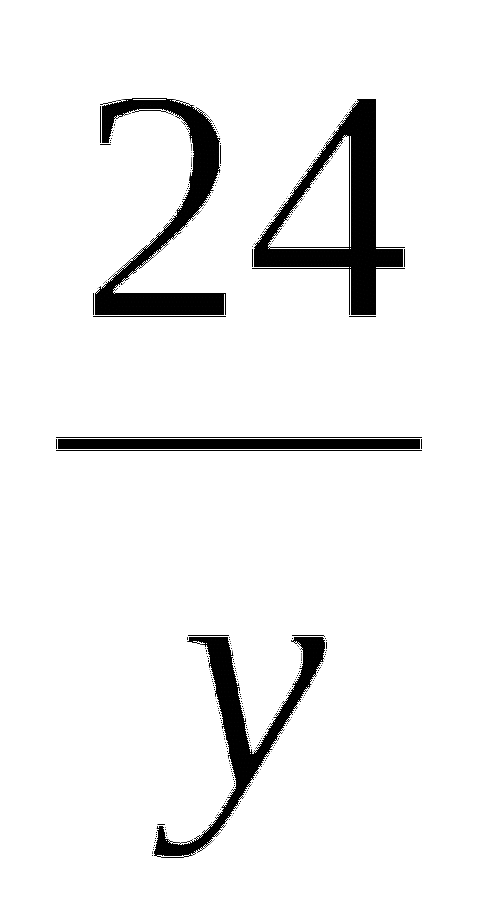 (-2; 12)
(-2; 12)
-
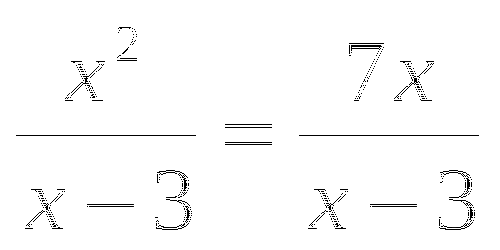 (0; 7)
(0; 7)
3. (х - 3)2 = 6 - 2х (1; 3)
2 группа
Решите уравнения:
-
(3х - 1) (2х - 2) = (х - 4)2 + 6 (2; - 2)
-
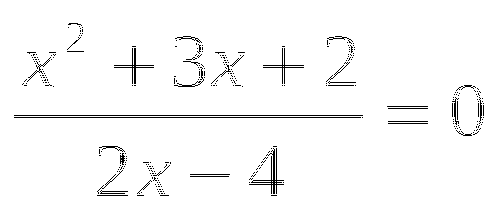 (-2; - 1)
(-2; - 1)
-
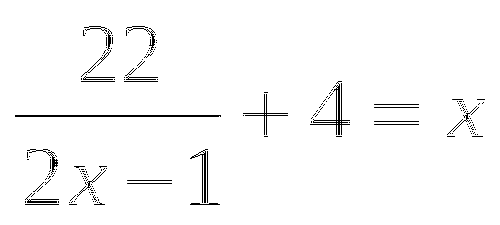 (-1,5; 6)
(-1,5; 6) -
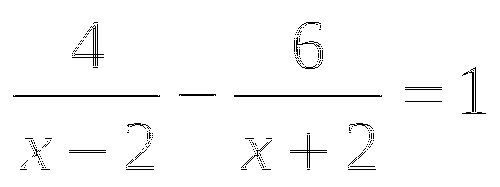 (-6; 4)
(-6; 4)

У древних греков существовала легенда. В незапамятные времена у царя эфиопов Цефея была красавица - жена - царица Кассиопея. Однажды Кассиопея имела неосторожность похвастаться своей красотой в присутствии нереид - жительниц моря. Обидевшись, завистливые нереиды пожаловались богу моря Посейдону, и он напустил на берега Эфиопии страшное чудище - Кита, опустошавшего страну. Цефей вынужден был, по совету оракула, отдать на съедение чудовищу свою любимую дочь Андромеду. Ее приковали к прибрежной скале. Каждую минуту Андромеда ожидала, что из морской пучины вынырнет Кит и проглотит ее. В это время герой Древней Греции Персей совершал один из своих подвигов: он проник на уединенный остров на краю света, где обитали три страшные женщины - горгоны с клубками змей на голове вместо волос. Взгляд Горгоны превращал в камень все живое. Воспользовавшись сном горгон, Персей отсек голову одной из них по имени Медуза. Из ее тела выпорхнул крылатый конь Пегас. Две другие горгоны, проснувшись, хотели броситься на Персея, но он вскочил на крылатого Пегаса и, держа в руках драгоценную добычу - голову Медузы, полетел домой.
Пролетая над Эфиопией, Персей заметил прикованную к скале Андромеду. К ней уже направлялся Кит, вынырнувший из морской пучины. Персей вступил в смертельный бой с чудовищем. Одолеть Кита удалось лишь после того, как на него упал леденящий взгляд мертвой головы Медузы. Кит окаменел, превратившись в небольшой остров. Персей расковал Андромеду, привел ее к Цефею, а впоследствии и женился на ней.
Главных героев этого мифа фантазия древних греков поместила на небо. Так появились названия созвездий Цефея, Кассиопеи, Андромеды, Персея, Пегаса, Кита.
-
Подведение итогов урока организуется в виде разгадывания кроссворда, состоящего из теоретических сведений, вопросов по теме «Квадратные уравнения».





































































































































-
Математик доказавший, что х1 + х2 = - р, х1 х2 = q
-
Название выражения b2 - 4ac
-
Квадратное уравнение в котором а = 1
-
Способ решения уравнения вида ах4 + bх + с = 0
-
Уравнение вида ах2 + bх + с = 0
-
Значение неизвестного, при котором уравнение обращается в верное числовое равенство
-
Число корней квадратного уравнения при D > 0
-
Что можно найти перемножив время и скорость?
-
Квадратное уравнение, где b или с равны нулю
-
Число корней квадратного уравнения при D = 0
-
Что можно найти, разделив пройденный путь на скорость?
-
Ключевое слово: Уравнение вида ах4 + bх + с = 0
 Домашнее задание: Индивидуальное задание по карточкам, творческое задание:
Домашнее задание: Индивидуальное задание по карточкам, творческое задание:
составить уравнения, корнями которого являются пары чисел (-5;0),
(-3; 2), (-1; 0), (1; 0), (3; - 2). (В результате на координатной
плоскости получится созвездие «Кассиопея»)
Решите уравнения:
-
у - 10 =
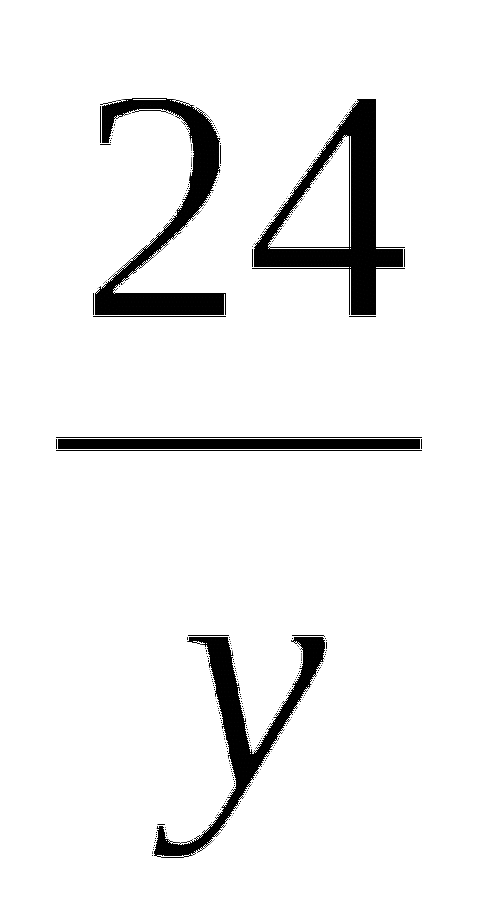 2.
2. 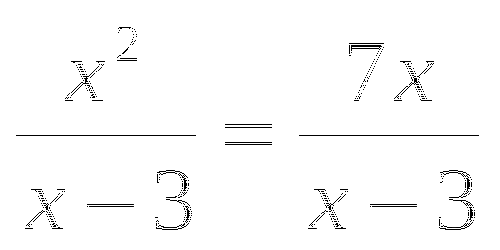 3. (х - 3)2 = 6 - 2х
3. (х - 3)2 = 6 - 2х
Решите уравнения:
-
(3х - 1) (2х - 2) = (х - 4)2 + 6
-
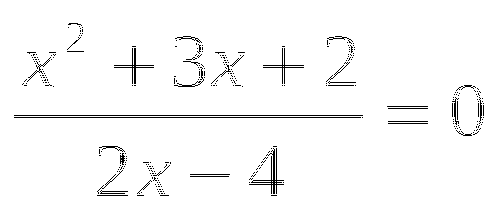
![]()
Решите уравнения:
-
у - 10 =
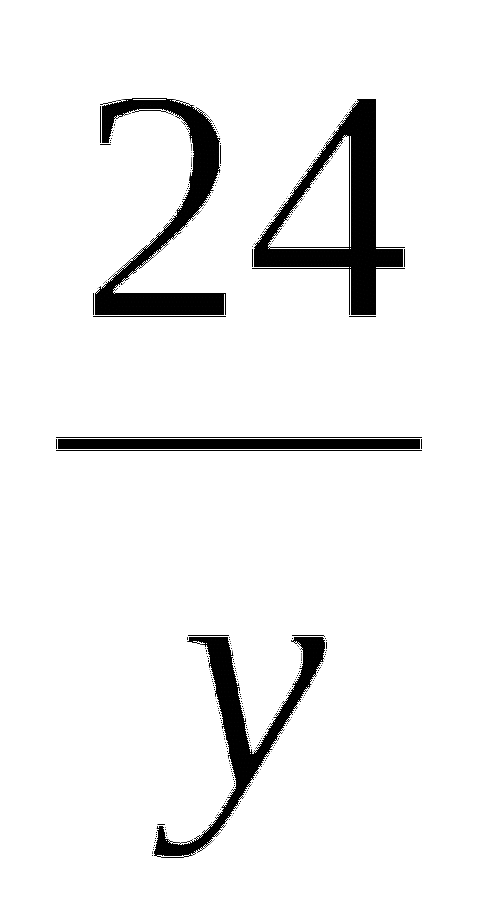 2.
2. 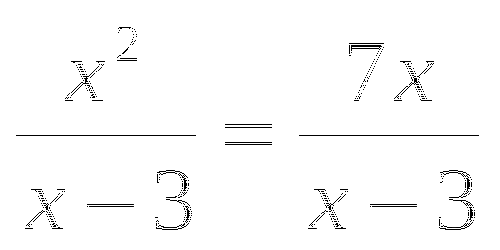 3. (х - 3)2 = 6 - 2х
3. (х - 3)2 = 6 - 2х
Решите уравнения:
-
(3х - 1) (2х - 2) = (х - 4)2 + 6
-
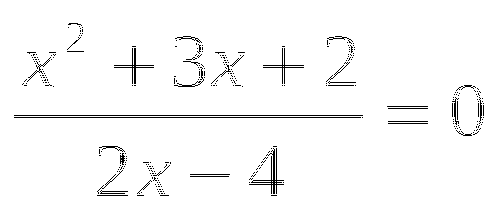
![]()
Решите уравнения:
-
у - 10 =
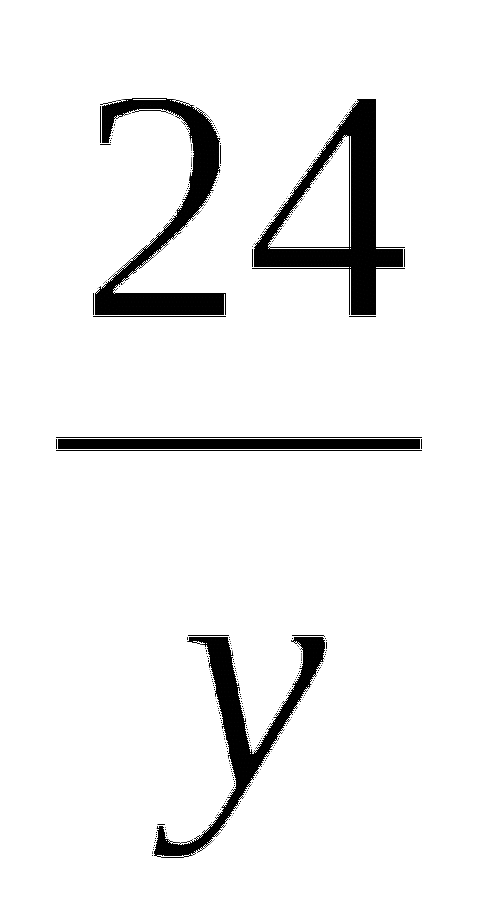 2.
2. 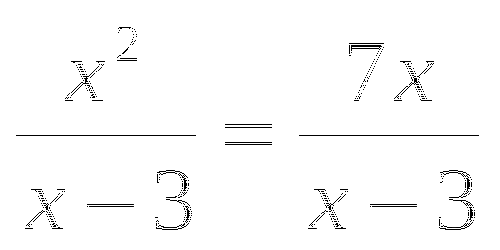 3. (х - 3)2 = 6 - 2х
3. (х - 3)2 = 6 - 2х
Решите уравнения:
-
(3х - 1) (2х - 2) = (х - 4)2 + 6
-
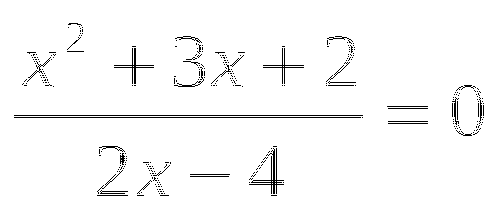
![]()
Решите уравнения:
-
у - 10 =
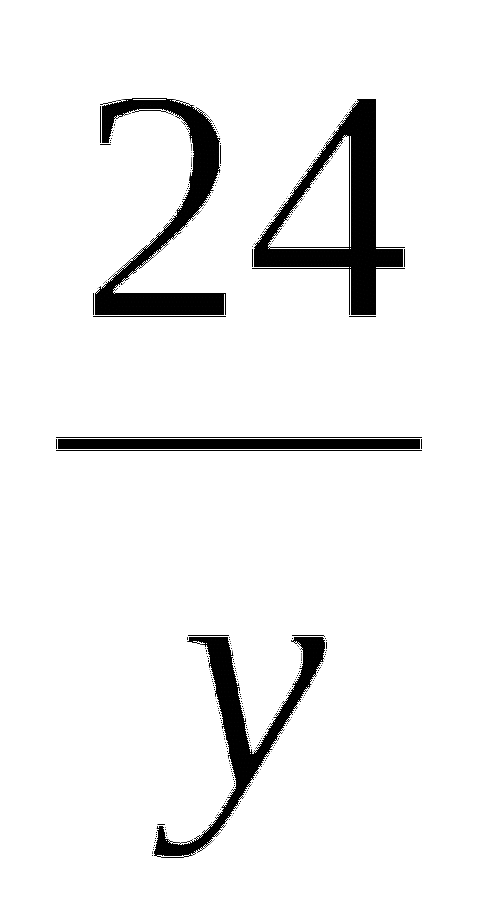 2.
2. 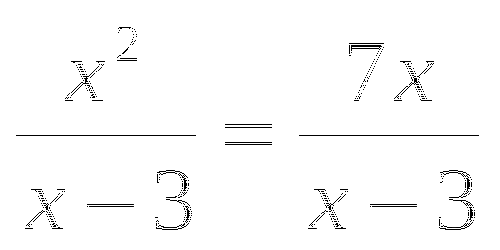 3. (х - 3)2 = 6 - 2х
3. (х - 3)2 = 6 - 2х
Решите уравнения:
-
(3х - 1) (2х - 2) = (х - 4)2 + 6
-
![]()