Открытый урок по математики на тему 'Задачи на проценты' (9 класс)

МКОУ «Зургановская средняя общеобразовательная школа»

Открытый урок

подготовки к ГИА по математике в 9 классе

Найминовой Галины Пюрвеевны.

Тема:«Проценты.
Основные задачи на проценты»

2014 год

Пояснительная записка

Краткое изучение темы «Проценты» в 5 классе не дает больших результатов. Учащиеся в силу возрастных особенностей еще не могут полноценное представления о процентах, об их роли в повседневной жизни. На последующих этапах обучения повторного обращения к этой теме не предусматривается. Поэтому задачи на проценты вызывают затруднения у учащихся и очень многие окончившие школу не имеют прочных навыков обращения с процентами в повседневной жизни. Кроме того текстовые задачи на проценты включены в материалы ГИА за курс основной школы, в КИМы и ЕГЭ. Предлагаю вашему вниманию урок (2ч) элективного курса по математике в 9 классе.

Тема: Проценты.
Основные задачи на проценты.

Ц е л и: сообщить краткую историю появления процентов; привести примеры повседневного использования процентных вычислений в настоящее время; устранить пробелы в знаниях по решению основных задач на проценты: нахождение процента от величины, нахождение величины по ее проценту, нахождение процента одной величины от другой; ввести понятия «простой процентный рост», «сложный процентный рост»; решение основных задач на проценты

Методы обучения: беседа, объяснение, устные упражнения, письменные упражнения.

Формы контроля: проверка самостоятельной работы.

Х о д з а н я т и я

I. Краткая история появления процентов

Проценты - одно из математических понятий, которые часто встречаются в повседневной жизни. Так, мы часто читаем или слышим, что, например, в выборах приняли участие 69 % избирателей, уровень инфляции составляет 7 % в год, молоко содержит 3,2 % жира и т. д.

Если речь идет о проценте от данного числа, то это число и принимается за 100 %. Например, 1 % от зарплаты - это сотая часть зарплаты; 100 % зарплаты - это сто сотых частей зарплаты. Т. е. вся зарплата. Подоходный налог с зарплаты берется в размере 13 %, т. е. 13 сотых от зарплаты. 3,2 % жира в молоке означает, что 3,2 сотых массы продукта составляет жир (или, другими словами, в каждых 100 граммах этого продукта содержится 3,2 грамма жира).

II. Повторение и закрепление.

1) Основные сокращенные процентные отношения.

200 % = 2; 25 % =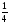

100 % = 1; 10% =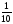

50 % =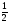; 1 % =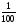

2) Р а з л и ч н ы е о б о з н а ч е н и я:

1 %

0,01

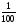
18 %

0,18

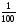
р %

0,01р

III. Устная работа

1) Представьте данные десятичные дроби в процентах:

Пример: 0,08 = 0,08 х 100% = 8 %

а) 0,6; б) 0,231; в) 2,34.

нахождение процентов данного числа

Чтобы найти р % от а , надо а ·0,01р.

Пример. 15 % от 90 составляет: 15% = 15:100 = 0,15

90·0,15 = 13,5.

Ответ: 13,5.

2) Представьте проценты десятичными дробями:

Пример: 5% = 5% : 100% = 0,05

4 %; 12,5 %; 0,06 %; 1000%

3) Найти:

10% от 60 руб,

50% от 200 руб,

200% от 200 л.

4) найдите процентное отношение чисел:

а) 60 и 240, б) 40 и 200.

2) Нахождение числа по его процентам.

Если известно, чтор % числа а равно в, то а = в : 0,01 р

П р и м е р. 2 % числа х составляют 140.

2% = 2:100 = 0,02

а = 140 : 0,02;

а = 7000.

Ответ: 7000

3) Нахождение процентного отношения чисел.

Чтобы найти процентное отношение чисел, надо отношение этих чисел умножить на 100 %:

.

Пример. В 180г воды растворили 20г соли. Найдите процентное содержание соли в растворе.

Решение: 20/180 100 = 90.

IV. Решение основных задач на проценты.

1. Простые проценты.

1) Одна величина больше (меньше) другой на р %.

а - первоначальное значение

р - количество процентов

в - новое значение

а) если а возросло на р %, то новое значение равно

в = а(1 + 0,01р).

б) если а уменьшили на р %,то новое значение равно

в= а(1 - 0,01р).

в) если а сначало уменьшили на р%, затем полученное число увеличили

на р%, то новое значение равно

в = а(1 - 0,01р) (1 + 0,01р) = а(1 -(0,01р)²) (*)

Пример 1.

Увеличить число 60 на 20%.

Решение:

60(1+ 0,0120) = 60(1+ 0,2) = 60 1,2 = 72.

Ответ: 72

Пример 2. ( ГИА - 2011)

На мебельном магазине старые цены заменены новыми. На сколько примерно процентов снижены цены при распродаже мебели?

Цена

Шкаф

Кровать

Стол

Старая

3999 руб.

1205 руб.

1000 руб.

Новая

3000 руб.

900 руб.

752 руб.

А. Примерно на 30%

Б. Примерно на 20%

В. Примерно на 25%

Г. Примерно на 80%

Решение:

Шкаф - 3000=3999· (1-р)

р = 999: 3999

р = 0,249= 25%

Стол - 752 = 1000 · ( 1 - р )

р = 248 : 1000

р = 0,248= 25%

Ответ: В

Пример3.

Цену товара снизили на 30 %, затем новую цену повысили на 30 %. Как изменилась цена товара?

Р е ш е н и е.

Пусть первоначальная цена товара а, тогда:

а - 0,3а = 0,7а - цена товара после снижения,

0,7а + 0,7а ·0,3 = 0,91а - новая цена.

1,00 - 0,91 = 0,09 или 9 %.

Используя формулу (*), получим:

О т в е т: цена снизилась на 9 %.

Пример 4. (ЕГЭ - 2010)

Магазин закупает цветочные горшки по оптовой цене 100 руб за штуку.

Торговая надценка составляет 25%. Какое наибольшее число таких

горшков можно купить в этом магазине на 1300 рублей.

Решение:

Пусть новая цена горшков будет в

в = 100 (1 + 0,25) = 125 р

1300 : 125 =10,4

Можно купить 10 горшков

Ответ: 10

2. Сложные проценты.

а - первоначальное значение величины;

в - новое значение величины;

р - количество процентов;

п - количество промежутков времени.

в = а (1 + 0,01р)^п,

Если изменение происходит на разное число процентов, то формула выглядит так

в = а·(1 + 0,01р₁)(1 + 0,01р₂) … (1 + 0,01р_п)

Пример 1.

Санж, открыл счет в банке, внеся 2000 р. на вклад, годовой доход по которому составляет 12% и решил в течение 3 лет не брать процентные начисления. Какая сумма будет лежать на его счете через 3 года.

Решение:

в = а · ( 1 + 0,12 )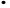

в = 2000 · ( 1 + 0,12 )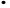 = 2808 руб.

Ответ: 2808 руб.

Пример 2. ( ГИА - 2011)

Летом рюкзак стоил 880 руб. Осенью цены на рюкзаки снизились на 25%. А зимой еще на 25%. Сколько рублей заплатит покупатель, если купит рюкзак зимой?

А. 830 руб Б. 660 руб В. 495 руб Г. 165 руб.

Решение:

Первоначальная цена - 880 руб

Пусть новая цена будет в руб

в = 880 ( 1 - 0,25) ( 1 - 0,25) = 880 ( 1- 0,25)= 495 р.

О т в е т: В

V. Самостоятельная работа

1. Найти 1 % от 6 тыс. жителей;

А. 0,06 Б. 60 В. 600 Г. 6

2. Сколько процентов составляют 15 г от 1 кг

А. 0,015% Б. 15% В. 0,15% Г. 1,5%

3.( ГИА - 2008 )

В таблице приведена стоимость работ по покраске потолков.

Цвет

потолка

Цена в рублях за 1 кв.м.

(в зависимости от площади помещения)

до 20 м

от 21до 40 м

от 41до 60 м

свыше 60 м

белый

120

105

90

75

голубой

140

125

110

90

Пользуясь данными, представленными в таблице, определите, какова будет стоимость работ, если площадь потолка 40 м, потолок голубой, и действует сезонная скидка 10%.

А. 4950р Б. 5000р В. 4500р Г. 500р

4. Ученик прочитал в первый день 15 % книги, что составило 60 страниц, во второй день он прочитал 200 страниц. Сколько страниц ему осталось прочитать?

О т в е т:

5. Цена на бензин в первом квартале увеличилась на 20 %, а во втором - на 30 %. На сколько процентов увеличилась цена на бензин за два квартала?

А. 50% Б. 10% В. 56% Г. 65%

6. ( ГИА -2011, Зад. № 20)

Сосна на 50% выше ели. Если каждое дерево подрастет еще на 10м, то сосна будет выше ели на 25%. Найдите первоначальную высоту ели.

Ответ:

Домашнее задание. № 59, 65. Составить задачи, используя жизненные ситуации, записать на отдельных листах.