- Учителю
- Урок математики в 8 классе на тему
Урок математики в 8 классе на тему
Подготовила : учитель
математики
Андрющенко И. П.
"Решение квадратных уравнений"
Тип урока: обобщение изученного материала.
Цели урока:
-
обобщить изученный по теме материал;
-
формировать умения применять математические знания к решению практических задач;
-
развивать познавательную активность, творческие способности;
-
воспитывать интерес к предмету.
Оборудование и материалы:
-
Карточки-задания для устной и индивидуальной работы.
-
Сообщения учащихся (исторические сведения).
Ход урока:
I. Организационный момент.
Цель: формирование мотива, желания работать на уроке.
II. Теоретическая разминка.
Цель: повторение необходимых теоретических сведений по теме, развитие умений говорить и слушать.
1. Дайте определение квадратного уравнения.
2. Назовите виды уравнений, записанных на доске.
2x2 + 6x + 5 = 0
x2-7x +10 = 0
3x2 - 25x + 28 = 0
2x2 + 4x = 0
4x2 - 25 = 0
x2 - 64 = 0
3. Ход решения уравнений.
3х2 + 4х = 0
х(3х + 4) = 0 х2 -64 = 0
х = 0 или 3х + 4 = 0 х2 = 64
3х = -4 х1 = -√64
х = -4/3 х2 = √64
х = -1 1/3 х1 = -4
х2 = 4
Решение комментируют учащиеся.
Учащиеся ход решения записывают в тетради, а учитель на доске.
Проверяются знания определения квадратного уравнения, его видов, умение различать квадратное уравнение среди других видов.
III. Индивидуальная работа по карточкам
Цель: проверка необходимых умений различать квадратное уравнение среди других видов, определять вид квадратного уравнения, определять коэффициенты квадратного уравнения.
Карточка №1:
Выбери из представленных в задании уравнений те, которые являются квадратными:
-
12х2-0,3=(0,4х2-2)30 6. 6х-8=х(1,5+2х)
-
4+1,3х2=0 7. х2=0
-
(х-3)(х-5)=2х 8. х(х-2,6)(х-1)=0
-
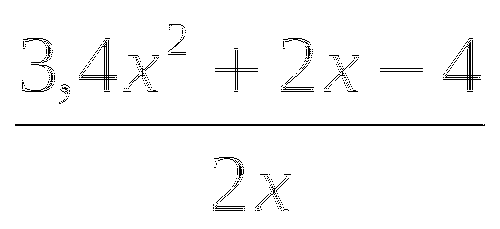 =0 9.
=0 9. 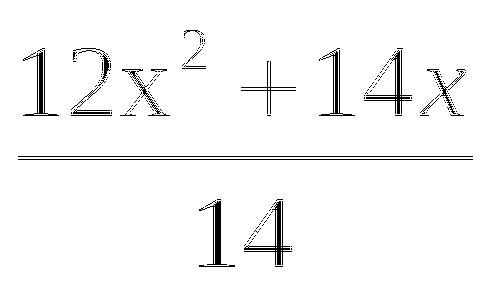 -2,8х=14,7
-2,8х=14,7 -
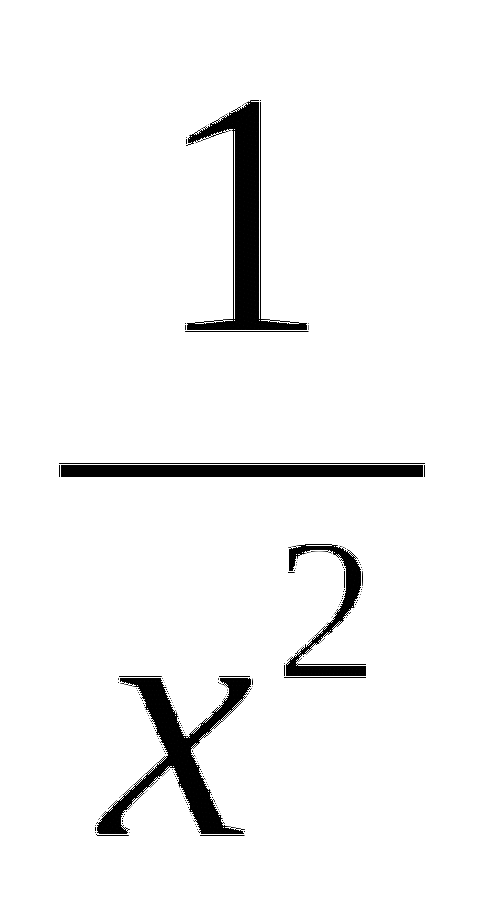 +48х=х2-10 10. 8х4-2,3х2+10=0
+48х=х2-10 10. 8х4-2,3х2+10=0
Карточка №2:
Определи вид квадратного уравнения:
-
1,3х2=4
-
3х2=0
-
(х-3)(х-5)=2х
-
(12х-3)(х-5)=2х
-
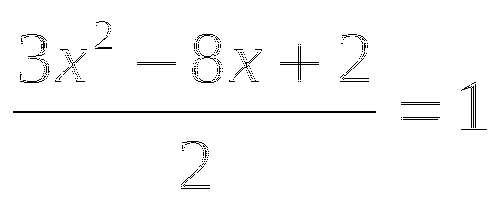
Карточка №3:
Определите коэффициенты квадратного уравнения:
а) 6х2 - х + 4 = 0
б) 12х - х2 + 7 = 0
в) 8 + 5х2 = 0
г) х - 6х2 = 0
д) - х + х2 = 15
Каждый учащийся получает карточку с индивидуальным заданием (задания различного уровня сложности), после окончания работы сдаются на проверку учителю.
IV. Совместная работа учителя с классом
Цель: повторение способов решения:
полных квадратных уравнений.
РЕШИ УРАВНЕНИЯ с помощью формулы:
1 вариант: а) -7х + 5х2 + 1 =0
б) (х - 1)(х + 1) = 2 (5х - 10,5)
2 вариант: а) 2х2 + 5х -7 = 0
б) -х2 = 5х - 14
3 вариант: а) х2 - 8х + 7 = 0
б) 6х - 9 = х2
Карточка №4:
Реши уравнения с помощью теоремы Виета:
-
х2 - 9х + 20 = 0
-
х2- 19х + 88 = 0
-
х2+ 16х + 63 = 0
-
В уравнении х2+ рх + 56 = 0 один из корней равен 7.
Найди другой корень и коэффициент р.
На данном этапе организуется фронтальная работа по повторению способов решения квадратных уравнений.
Затем учащимся предлагается выбрать уровень по своему усмотрению, решить самостоятельно уравнения и оценить себя.
V. Исторические сведения
Цель: формирование учебно-познавательной мотивации школьников на уроке, воспитание интереса к предмету.
Исторические сведения:
Квадратные уравнения впервые встречаются в работе индийского математика и астронома Ариабхатты.
Другой индийский ученый Брахмагупта (VII в) изложил общее правило решения квадратных уравнений, которое практически совпадает с современным.
В Древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто облекались в стихотворную форму.
Франсуа Виет
Жизнь Виета представляет для нас интерес во многих отношениях.
XV век в Западной Европе был веком ожесточенных религиозных волнений, и к началу XVI целый ряд стран отпал от католической церкви.
Всесильная католическая церковь преследовала и убивала всякую мысль, в которой усматривала отклонение от своих учений. Церковный суд - инквизиция - всех попавшихся под подозрение карал вплоть до сожжения на костре, а имущество казненных отбирал в пользу церкви. Не один ученый погиб в руках инквизиции. В их числе были и математики.
Испанский математик Вальмес в 1486 году как-то в семейном кругу обмолвился о том, что нашел формулу для решения уравнения четвертой степени. В числе гостей оказался влиятельный инквизитор. Услышав слова Вальмеса, он заявил, что волей Божьей решать эти уравнения человеку не дано, а найти формулу можно было только с помощью дьявола.
В ту же ночь Вальмес был брошен в тюрьму, а через три недели сожжен на костре за связь с дьяволом. Лишь через 100 лет решение этих уравнений было найдено вторично.
Мэтр Виет также был на волосок от костра.
В ту пору наиболее могущественное государство в Европе, Испания вела победоносную войну с Францией.
Однажды французам удалось перехватить приказы испанского правительства командованию своих войск, написанные очень сложным шифром (тайнописью). Виет с помощью математики сумел найти ключ к этому шифру. С этих пор французы, зная планы испанцев, с успехом предупреждали их наступления.
Инквизиция обвинила Виета в том, что он прибегнул к помощи дьявола, и приговорила к сожжению на костре. Но так как французы благодаря Виету в дальнейшем побеждали, он не был выдан инквизиции.
В родном городке Виет был лучшим адвокатом, а позднее стал королевским советником. Но главным делом его жизни была математика. Биографы Виета пишут, что он мог несколько ночей подряд не спать, решая очередную математическую задачу.
Вот задача Бхаскары:
Обезьянок резвых стая, всласть поевши, развлекалась.
Их в квадрате часть восьмая на полянке забавлялась.
А двенадцать по лианам стали прыгать, повисая.
Сколько ж было обезьянок, ты скажи мне, в этой стае?
Р![]() ешение задачи Бхаскары:
ешение задачи Бхаскары:
Пусть было x обезьянок, тогда на поляне забавлялось - .
Составим уравнение:
![]()
+ 12 = х
На данном этапе учащимся сообщается материал из истории возникновения квадратных уравнений, сведения об известном французском математике Франсуа Виете. (Сообщения готовили учащиеся)
Затем учащимся предлагается решить самостоятельно задачу Бхаскары.
VI. Подведение итогов урока.
При подведении итогов урока подчеркивается, что серьезное отношение к теории помогает углубить и расширить круг упражнений и задач по теме.
VII. Домашнее задание: Подготовка к контрольной работе.