Конспект урока по геометрии в 8 классе

Урок геометрии. 8 класс.

Тема урока «Решение задач по теме «Площади фигур».

Тип урока (УОИСЗУ)- урок обобщения и систематизации знаний и умений.

Цель урока: 1.Закрепить теоретический материал по теме «Площадь» ; 2. Совершенствовать навыки решения задач на вычисление площадей.

Задачи:

Личностные: создание условий формирования у обучающихся положительной мотивации к учению; умение преодолевать посильные трудности; чувство коллективизма, взаимовыручки и уважения друг друга.

Метапредметные: формирование умения классифицировать объекты, повышать алгоритмическую культуру обучающихся, развивать логическое мышление, познавательную активность, навыки устной речи.

Предметные: формировать умения построения математической модели, решения уравнений, совершенствовать вычислительные навыки.

Форма обучения: фронтальная, групповая.

Этапы урока

1. Организационный момент.

Сообщить тему урока, сформировать цели урока.

2. Актуализация знаний учащихся.

Проверка домашнего задания. Проверить решение задачи №478. Один из учащихся заранее готовит решение задачи на доске.

Наводящие вопросы:

• Существует ли формула для вычисления площади произвольного четырехугольника?

• Какие способы вычисления площадей вам известны?

• На какие геометрические фигуры, площади которых вычисляются по известным нам формулам, разбит выпуклый четырехугольник?

• Как вычислить площадь каждой фигуры? А площадь всего четырехугольника?

• Упростите полученное выражение.

Теоретический тест.

Работа выполняется в тетради по вариантам. По окончанию работу учащиеся меняются тетрадями, проверяют сами по заранее подготовленным ответам, выведенными на экран через мультимедийную установку

ТЕСТ.

1 вариант.

1. Выберите верные утверждения:

а) площадь прямоугольника равна произведению двух его сторон;

б) площадь квадрата равна квадрату его стороны;

в) площадь прямоугольника равна удвоенному произведению двух его соседних сторон.

2. Закончите фразу: «Площадь ромба равна половине произведения….

а) его сторон;

б) его стороны и высоты, проведенной к этой стороне;

в) его диагоналей.

3. По формуле S=a∙h_a можно вычислить площадь:

а) параллелограмма;

б) прямоугольника;

в) треугольника.

4. Площадь трапеции ABCD с основаниями AB и CD и высотой BH вычисляется по формуле:

а) S= AB : 2∙CD∙BH;

б) S= (AB+BC) :2 BH;

в) S= (AB + CD) : 2 ∙ BH .

5. Выберите верное утверждение.

Площадь прямоугольного треугольника равна:

а) произведению его стороны на проведенную к ней высоту;

б) половине произведения его катетов;

в) половине произведения его стороны на какую-нибудь высоту.

6. В треугольниках ABC и MNK B = ∟N. Отношение площадей треугольников ABC и MNK равно:
   
   

   а

   б

   в

   

   

   

   
   
   

   
   

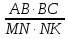
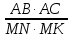
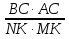
7. В треугольниках MNK и POS высоты NE и OT равны. Тогда S_MNK : S_POS = …

а) MN : PO; б) MK : PS в) NK : OS

2 вариант.

1. Выберите верные утверждения:

а) Площадь квадрата равна произведению его сторон.

б) Площадь прямоугольника равна произведению его противоположных сторон.

в) Площадь прямоугольника равна произведению двух его соседних сторон.

2. Закончите фразу : «Площадь параллелограмма равна произведению…

а) двух его соседних сторон;

б) его стороны на высоту, проведенную к этой стороне;

в) двух его сторон.

3. По формуле S= d₁d₂: 2 можно вычислить площадь:

а) параллелограмма;

б) треугольника;

в) ромба.

4. Площадь трапеции ABCD с основаниями BC и AD и высотой CH вычисляется по формуле:

а) S=CH ∙ (BC + AD) : 2;

б) S= (AB+BC) CH : 2 ;

в) S= (BC + CD) ∙ CH : 2.

5. Выберите верное утверждение.

Площадь треугольника равна:

а) половине произведения его сторон;

б) половине произведения двух его сторон;

в) произведению его стороны на какую-либо высоту.

6. В треугольниках ABC и DEF C = ∟F. Отношение площадей треугольников ABC и DEF равно:

а

б

в

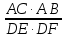
7. В треугольниках DEF и TRQ высоты DA и TB равны. Тогда S_DEF : S_TRQ = …

а) EF : RQ; б) DE : TR в) EF : RT.

3. Решение задач.

Работа в тетрадях. Проверка осуществляется через мультимедийную установку.

1. В трапеции ABCD одно из оснований в 3 раза меньше другого, а высота составляет 75% большего основания. Площадь трапеции равна 72 см². Найдите основание и высоту трапеции.

Наводящие вопросы:

• Какая формула используется для вычисления площади трапеции?

• Выразите основания и высоту трапеции через переменную х и составьте уравнение, используя условие задачи.

2. В параллелограмме ABCD на стороне AD отмечена точка M такая, что

AM : MD = 3 : 2. Найдите площадь ΔABM , если площадь параллелограмма равна 60 см².

Наводящие вопросы:

• Разбейте параллелограмм ABCD на фигуры, площади которых можно вычислить.

• Какую часть занимает ΔBMC от параллелограмма?

• Чему равно отношение площадей треугольников ABM и CDM?

• Найдите площадь треугольника ABM.

4. Подведение итогов урока.

Оценить работу учащихся.

«Рефлексивный экран»

Ученики по очереди высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске:

• Сегодня я узнал…

• Было интересно…

• Было трудно…

• Я выполнил задания…

• Я понял, что…

• Теперь я могу…

• Я почувствовал, что…

• Я приобрел…

• Я научился…

• У меня получилось…

• Я смог…

• Я попробую…

• Меня удивило…

• Урок дал мне для жизни…

• Мне захотелось…

Домашнее задание: повторить теорию стр. 117-125, №466, 467, 476(б)

Дополнительная задача: В равнобедренной трапеции ABCD проведены высоты BK к стороне AD и высота DH к стороне BC. Найдите площадь четырехугольника BKDH, если площадь трапеции равна 89 дм².

Литература:

1. Геометрия. 7-9 классы: учебник для общеобразовательных учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. М.:Просвещение, 2013.

2. Поурочные разработки по геометрии: 8 класс- 2-е изд,перераб. И доп. - М.: ВАКО, 2006/ Н. Ф. Гаврилова.