Конспект урока Производная 10 класс

Применение производной к исследованию функции

Цели: формировать умение определять характер монотонности и экстремума с применением производной, развивать навык чтения графиков функции и производной функции, отрабатывать навык решения заданий типа В8 и В14 ЕГЭ; воспитывать ответственность за результат своего труда.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Проверка домашней работы (взаимопроверка)

2. Устный опрос по теории:

• Как определить характер монотонности с применением производной;

• По какому алгоритму следует определять характер монотонности

• Какие точки называются точками экстремума;

• Как найти экстремум функции

• Какая точка называется максимум (минимум) функции;

• Как найти максимум (минимум функции)

3. Решение задач типа В8 ЕГЭ (ответы записывают в тетради, потом самопроверка по образцу)

№ 27505 На рисунке изображены график функции у = f(x) и касательная к нему в точке с абсциссой х₀ . Найдите значение производной функции f(x) в точке х₀.

№ 317647 На рисунке изображён график функции у = f(x) и девять точек на оси абсцисс. В скольких из этих точек производная функции у = f(x) отрицательна?

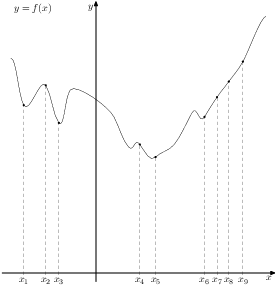
№ 317549 На рисунке изображён график функции у = f(x) и шесть точек на оси абсцисс. В скольких из этих точек производная функции у = f(x) положительна?

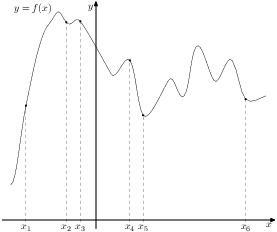
№ 6877 На рисунке изображен график функции у = f(x), определенной на интервале (-2; 11) . Определите количество целых точек, в которых производная функции положительна.

№ 7801 На рисунке изображен график у = f `(x) - производной функции у = f(x), определенной на интервале (-7;14). Найдите количество точек максимума функции у = f(x), принадлежащих отрезку [-6; 9] .

№ 7803 На рисунке изображен график у = f `(x) - производной функции у = f(x), определенной на интервале (-18;6). Найдите количество точек минимума функции у = f(x), принадлежащих отрезку [-13; 1] .

№ 8053 На рисунке изображен график у = f`(x) - производной функции у = f(x), определенной на интервале (-1;13). Найдите промежутки возрастания функции у = f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

№ 27490 На рисунке изображен график функции у = f(x), определенной на интервале (-2; 12) . Найдите сумму точек экстремума функции у = f(x).

4. Индивидуальные задания (во время устной работы)

№ 866(в), 867 (б), 868(в)

III. Работа по теме урока.

Все задания можно разбить на две группы.

1-я группа. Работа с графиками функций и графиками их производных с целью нахождения точек экстремума: № 30.17 - 30.20 (№873 - №876)

2-я группа. Нахождение точек экстремума функций по алгоритму.

1. № 30.28 (в) (№ 884(а))

№ 30.29 (б). (№885(б))

Необходимо следить за тем, чтобы на первых порах учащиеся вели подробные записи, строго следуя алгоритму.

Решение:

№ 30.29 (б).

1)

2)

х = 0, х = -1, х = 4

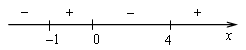
3)

4)

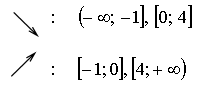
х = -1, х = 4 - точки минимума,

х = 0 - точка максимума.

Ответ:

2. № 30.30 (б). (886(б))

Решение:

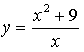
х = 0 - точка разрыва функции.

1)

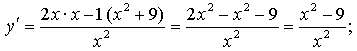
2)

3)

4)

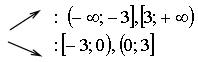
х = -3 - точка максимума;

х = 3 - точка минимума

Ответ:

3. № 30.31 (а). (№887 (а))

Решение:

Найдем область определения функции: х ≥ 2.

1)

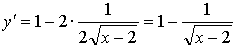
2)

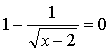
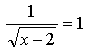
х = 3

3)

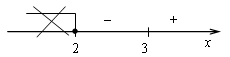
4)

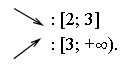
х = 3- точка минимума.

Ответ:

4. № 30.32 (б). (№888(б))

Решение:

1)

2)

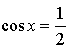
С учетом промежутка получим точки и

3)

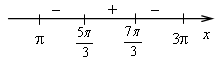
4)

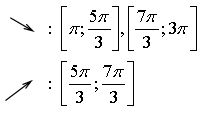
х = - точка минимума х = - точка максимума

Ответ: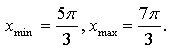

V. Итоги урока.

Вопросы учащимся:

- Какая точка называется точкой минимума (максимума) функции?

- Что можно сказать о производной в точке экстремума функции?

- Верно ли, что если в какой-то точке производная равна нулю, то эта точка является точкой экстремума функции?

- Сформулируйте достаточное условие экстремума.

- Сформулируйте алгоритм исследования непрерывной функции на монотонность и экстремумы.

- Могут ли быть экстремумы у функции вида 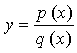в точках, обращающих знаменатель в нуль?

Домашнее задание: (группа 1): № 30.28 (г), № 30.29 (г), № 30.30 (а) (884(г), 885(г), 886(б))

(группа2): № 30.31 (б), № 30.32 (а) ( 887(б), 888(а)).¹

Задание части В (С - по желанию) варианта ЕГЭ.

1</ Номера заданий даны по разным годам издания (2009, 2005)