- Учителю
- Конспект урока по геометрии для 10 класса на тему Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости
Конспект урока по геометрии для 10 класса на тему Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости
Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости
Класс: 10
Цель урока:
образовательная: формировать понятие перпендикулярных прямых в пространстве, доказать лемму о перпендикулярности двух параллельных прямых к третьей прямой, дать определение перпендикулярности прямой и плоскости, доказать теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярностью к плоскости;
развивающая: развивать вычислительные навыки, логическое и пространственное мышление, речь учащихся;
воспитательная: воспитывать интерес к предмету, аккуратность при выполнении чертежей.
Тип урока: урок усвоения новых знаний
Методы обучения: индуктивно-эвристический, дедуктивно-репродуктивный.
Требования к ЗУН: учащиеся должны знать понятие перпендикулярных прямых в пространстве, доказательство леммы о перпендикулярности двух параллельных прямых к третьей прямой, определение перпендикулярности прямой и плоскости, формулировки теорем, в которых устанавливается связь между параллельностью прямых и их перпендикулярностью к плоскости; уметь применять изученные понятия и утверждения при решении задач по данной теме.
Оборудование: ПК, экран, проектор, мультимедиа презентация.
Литература:
-
Геометрия, 10-11: Учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. - 11-е изд. - М.: Просвещение, 2002 г.
-
Изучение геометрии в 10-11 классах: Метод. рекомендации к учеб.: Кн. для учителя /С. М. Саакян, В.Ф. Бутузов. - 2-е изд. - М. Просвещение, 2003. - 222 с.: ил. - ISBN 5-09-011836-1.
-
Методика и технология обучения математике. М.: Дрофа, 2005. - 416 с.
План урока:
I. Орг. момент (2 мин)
II. Изучение нового материала (20 мин)
-
Актуализация знаний.
-
Формирование понятия перпендикулярности двух прямых в пространстве.
-
Доказательство леммы о перпендикулярности двух параллельных прямых к третьей прямой.
-
Формирование понятия перпендикулярности прямой и плоскости.
-
Доказательство теорем, в которых устанавливается связь между параллельностью прямых и их перпендикулярностью к плоскости.
III. Первичное закрепление материала. №№ 117, 120 (17 мин)
IV. Подведение итогов (5 мин)
V. Домашнее задание. п.15 - 16, вопросы 1, 2 стр.54, №№ 116, 118 (1 мин)
ХОД УРОКА:
-
Орг. момент
Приветствие учеников, проверка готовности учащихся к уроку, проверка отсутствующих.
Учитель: (слайд 1) Мы приступаем к изучению новой большой главы: «Перпендикулярность прямых и плоскостей». Тема нашего сегодняшнего урока: «Перпендикулярность прямой и плоскости». Мы познакомимся с понятием перпендикулярных прямых в пространстве, с теоремами, касающимися перпендикулярности прямых и затем рассмотрим задачи.

Запись на доске и в тетрадях:
Число.
Классная работа.
«Перпендикулярность прямой и плоскости».
II. Изучение нового материала
1. Актуализация знаний.
Учитель: Какое взаимное расположение прямых на плоскости?
Ученик: Прямые могут не иметь общих точек - быть параллельными, иметь одну общую точку - пересекаться, либо быть перпендикулярными, иметь множество общих точек - совпадать.
Учитель: Какие прямые называются перпендикулярными на плоскости?
Ученик: Две прямые называются перпендикулярными, если при пересечении они образуют четыре прямых угла.
Учитель: Какое взаимное расположение прямых в пространстве?
Ученик: Две прямые могут пересекаться, быть параллельными, либо скрещивающимися.
2. Формирование понятия перпендикулярности двух прямых в пространстве.
Учитель: (слайд 2) Перед вами куб ABCDA1B1C1D1.
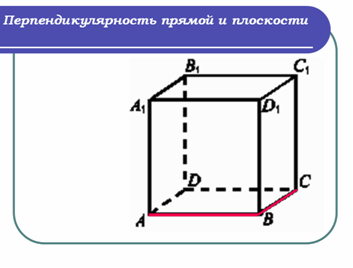
Учитель: Какое взаимное расположение прямых АВ и ВС?
Ученик: Прямые перпендикулярны.
Учитель: (слайд 2) Найдите угол между прямыми АА1 и DC.
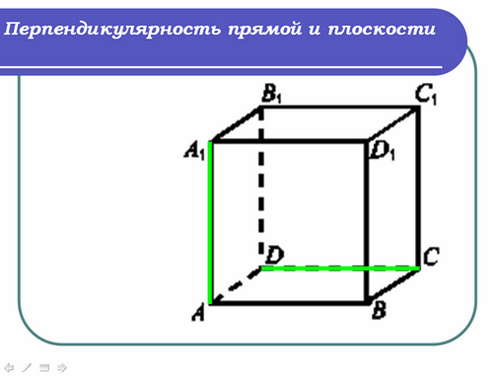
Ученик: Прямые АА1 и DC тоже перпендикулярны, угол между ними равен 90 градусов.
Учитель: (слайд 2) Запишем определение перпендикулярности двух прямых в пространстве
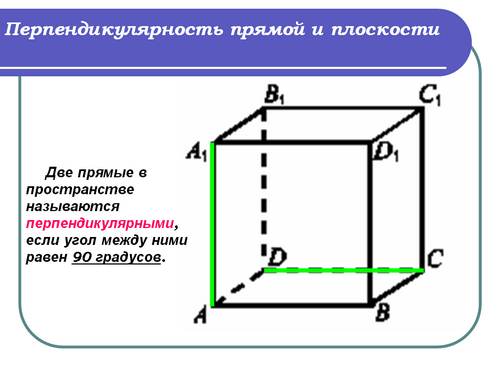
Запись в тетрадях:
Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90 градусов.
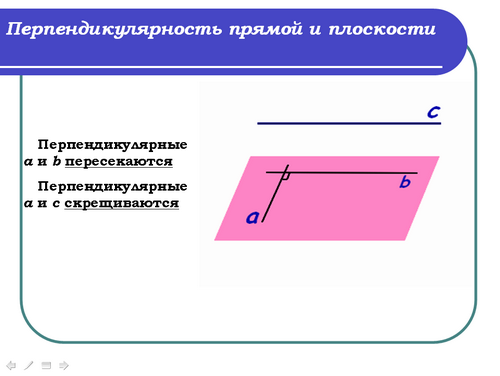
Учитель: (слайд 3) В пространстве перпендикулярные прямые могут пересекаться и могут быть скрещивающимися. Обратите также внимание на рисунок 43 на стр.34 ваших учебников. Перпендикулярные a и b пересекаются, а прямые a и c скрещиваются.
3. Доказательство леммы о перпендикулярности двух параллельных прямых к третьей прямой.
Учитель: (слайд 4) Рассмотрим прямые АА1 , СС1 и DC.
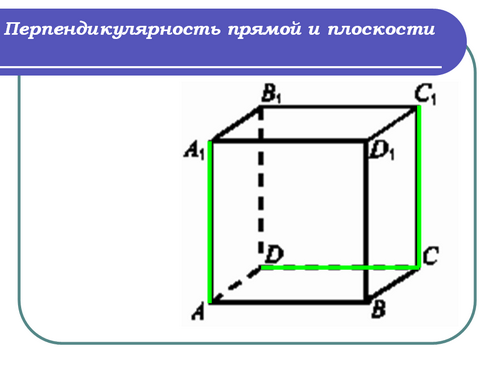
Учитель: Прямая АА1 параллельна прямой СС1, а прямая СС1 перпендикулярна прямой CD. Нами установлено, что АА1 перпендикулярна CD. Какой мы можем сделать из этого вывод? Сформулируйте это утверждение.
Ученик: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Учитель: (слайд 5) Это утверждение носит название Леммы о перпендикулярности двух параллельных прямых к третьей прямой.
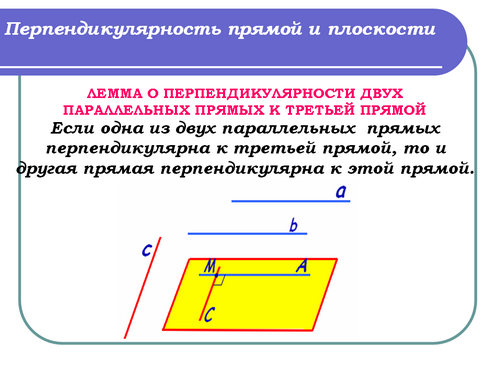
Запись в тетрадях:
Лемма. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Учитель: (слайд 6) Докажем лемму.

Запись на доске и в тетрадях:
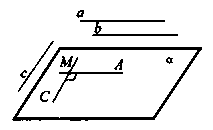
Дано: а || b, a ^. с
Доказать: b^с.
Учитель: Через точку М пространства, не лежащую на данных прямых, проведем прямые МА и МС, параллельные соответственно прямым а и с. Так как прямая a перпендикулярна c, то угол AMC равен 90 градусов.
Запись на доске и в тетрадях:
МА||а и МС||с. Т.к. a ^ c, то угол AMC = 90°
Учитель: По условию b||а, а по построению а || МА, поэтому b||МА. Итак, прямые b и с параллельны соответственно прямым МА и МС, угол между которыми равен 90°. Это означает, что угол между прямыми b и с также равен 90°, т. е. b ^ c.
Запись на доске и в тетрадях:
b||а (по условию), а || МА (по построению), => b||МА.
b|| МА и с|| МС, угол AMC = 90° => (b,^c) = 90°, т. е. b ^ c
4. Формирование понятия перпендикулярности прямой и плоскости.
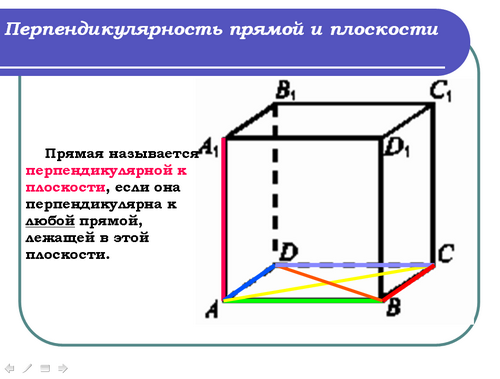
Учитель: (слайд 7) Рассмотрим куб ABCDA1B1C1D1. Найдем углы между прямой АА1 и прямыми плоскости АBCD.
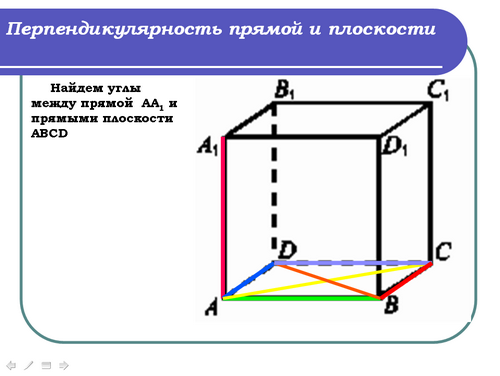
Ученик: Между прямой АА1 и прямыми плоскости АBCD углы равны 90°, т.е прямая АА1 перпендикулярна прямым плоскости АBCD.
Учитель: Отсюда мы можем сделать вывод: прямая АА1 перпендикулярна любой прямой, лежащей в плоскости АBCD. Такие прямые называются перпендикулярными. Перпендикулярность прямой α и плоскости α обозначается так: α ^ α,
Учитель: (слайд 7) Запишем определение прямой, перпендикулярной к плоскости:
Запись в тетрадях:
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
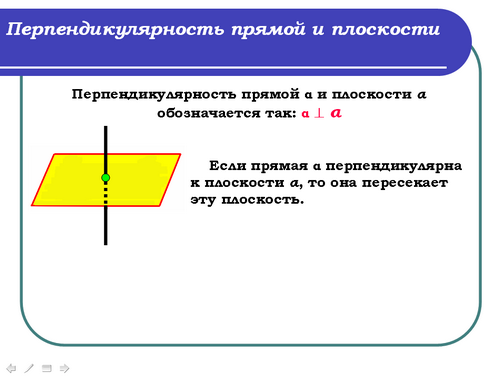
Обозначение: α ^ α
Учитель: Говорят также, что плоскость α перпендикулярна к прямой α.
Учитель: (слайд 8) Если прямая α перпендикулярна к плоскости α, то она пересекает эту плоскость. Действительно, если бы прямая α не пересекала плоскость α, то она или лежала бы в этой плоскости, или была бы параллельна ей, а это противоречит определению перпендикулярности прямой и плоскости, значит прямая α пересекает плоскость α.
Учитель: (слайд 9) На рисунке 45 стр.35 ваших учебников изображена прямая α перпендикулярная к плоскости α. Скажите, прямая будет перпендикулярна любой прямой, лежащей в плоскости α?
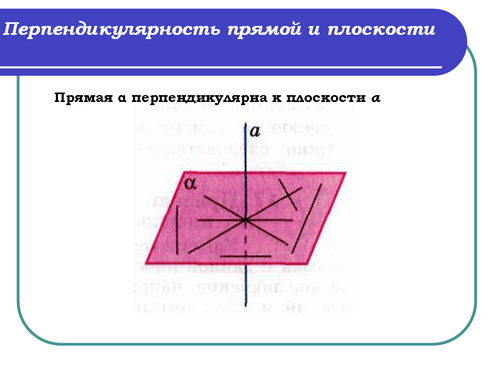
Ученик: Да, будет. Это следует из определения прямой, перпендикулярной к плоскости.
Учитель: (слайд 10) Окружающая нас обстановка дает много примеров, иллюстрирующих перпендикулярность прямой и плоскости. Прокомментируйте их.

Ученик: Телеграфный столб перпендикулярен к плоскости земли.. Так же расположены колонны здания по отношению к плоскости фундамента, линии пересечения стен по отношению к плоскости пола.
Учитель: А чему будет перпендикулярна открытая половинка окна?
Ученик: Плоскости подоконника, плоскости пола, плоскости потолка.
Учитель: Какие ещё примеры вы можете привезти из жизни?
Ученик: Люстра висит перпендикулярно к плоскости пола и плоскости потолка, горизонтальная линия доски перпендикулярна плоскости стены и т.д.
5. Доказательство теорем, в которых устанавливается связь между параллельностью прямых и их перпендикулярностью к плоскости.
Учитель: (слайд 11) Рассмотрим ещё две теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярностью к плоскости.
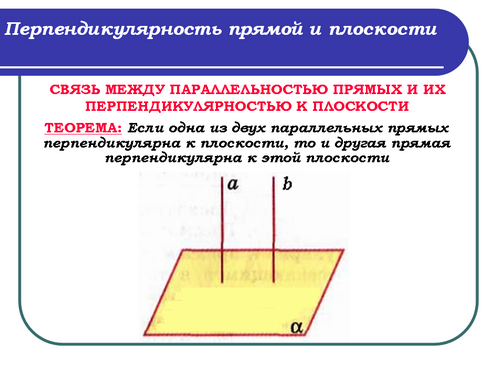
Запись в тетрадях:
Теорема: Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Учитель: (слайд 12) Докажем её.
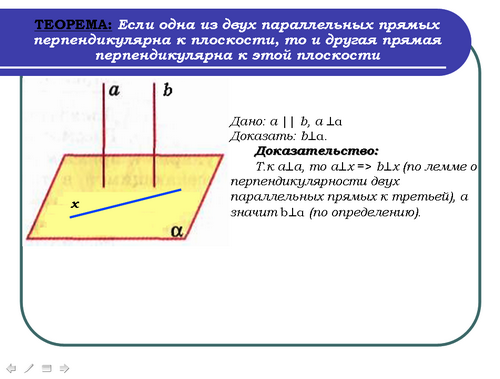
Запись на доске и в тетрадях:
Дано: а || b, a ^α
Доказать: b^α.
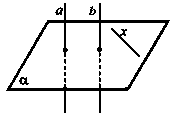
Учитель: Проведем какую-нибудь прямую х в плоскости α. Так как а^α, то а^х. По лемме о перпендикулярности двух параллельных прямых к третьей b^х.
Таким образом, прямая b перпендикулярна к любой прямой, лежащей в плоскости α, т.е. b^α.
Запись на доске и в тетрадях:
Т.к а^α, то а^х => b^х (по лемме о перпендикулярности двух параллельных прямых к третьей), а значит b^α (по определению).
Учитель: (слайд 13) Докажем обратную теорему.
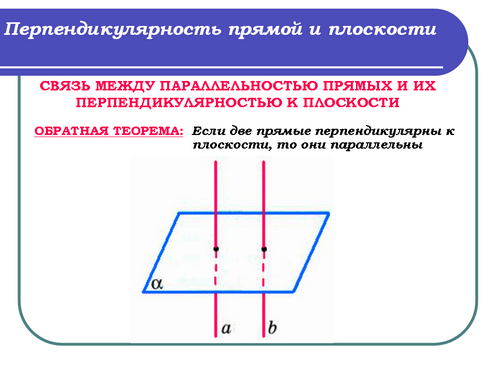
Запись в тетрадях:
Теорема: Если две прямые перпендикулярны к плоскости, то они параллельны.
Учитель: (слайд 14) Доказательство:
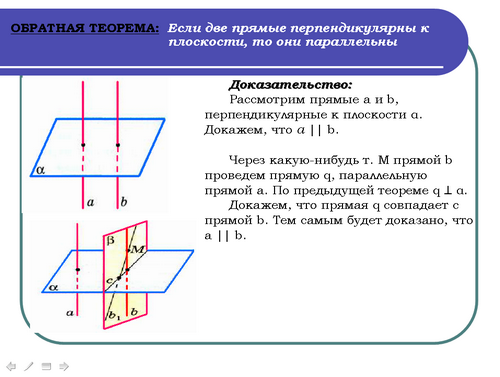
Учащиеся самостоятельно записывают доказательство в тетрадь.
III. Закрепление изученного материала
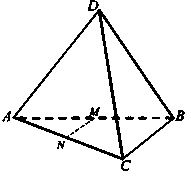
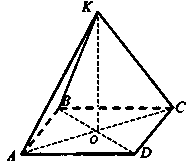
Учитель: Переходим к решению задач. №№ 117, 120
Один ученик работает у доски, остальные на местах в тетрадях.
Учитель: Что дано в задаче?
Учитель: Что нужно доказать?
Учитель: Как мы это докажем?
Учитель: Какие теоремы можно применить?


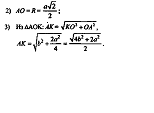
-
Подведение итогов
Обобщение материала, изученного на уроке, повторение основных понятий и формулировок (фронтальный опрос). Выделение положительных и отрицательных моментов урока, оценка работы ребят, выставление отметок.
-
Домашнее задание
Запись в дневниках
п.15 - 16, вопросы 1, 2 стр.54, №№ 116, 118