Факультативное занятие

в 11 классе.

Тема «Решение задач с параметрами»

Учитель математики

СОШ №1

Вакажева А. Х.

а. Кошехабль

Решение задач с параметрами.

План факультативного занятия.

Тема. Задачи с параметрами.

Ход занятия.

1. Объяснение материала.

Можно начать с рассмотрения следующих примеров:

• прямая пропорциональность: у = kх (х и у переменные, k ­- параметр, k;

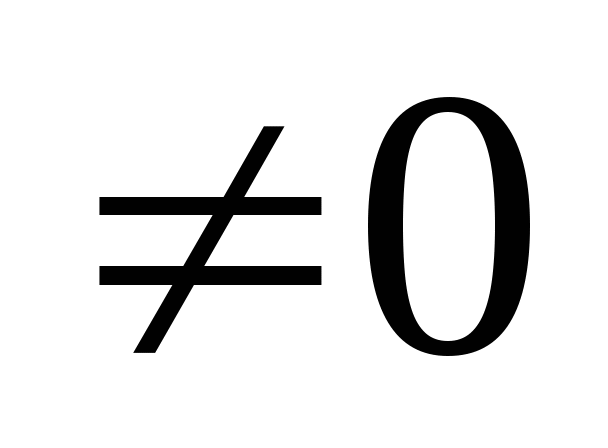• линейная функция: у = kх + b (x и y - переменные, k и b -параметры);

• уравнение первой степени: ах + b + c = 0 (х - переменная, a, b,c-параметры, а);

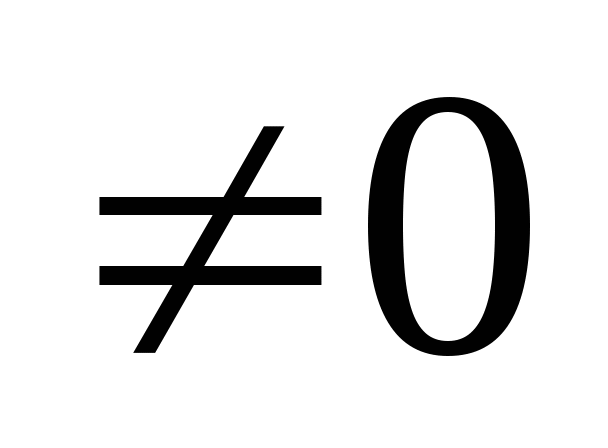• квадратное уравнение ax² + bx + c = 0 (x - переменная,a,b и c - параметры, a.

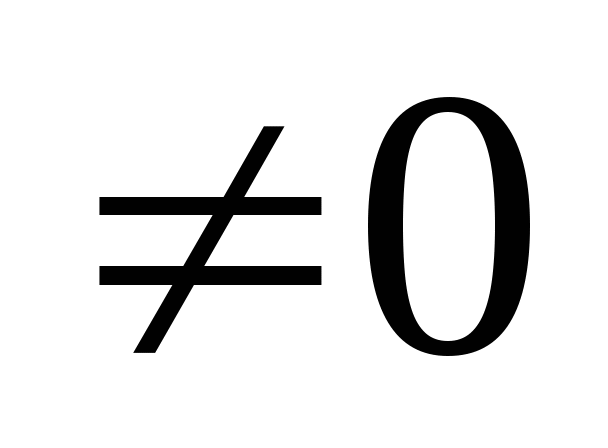В школьном курсе рассматриваются такие задачи как поиск решений линейных и квадратных уравнений в общем виде, исследование количества их корней в зависимости от значений параметров.

При решении задач с параметрами необходимо усвоить следующее: параметр будучи фиксированным, но неизвестным числом, имеет как бы двойственную природу. Во-первых, предполагаемая известность позволяет «общаться» с параметром как с числом; во-вторых, степень свободы общения ограничивается его неизвестностью.

Основное, что нужно усвоить при первом знакомстве с параметром, - это необходимость осторожного обращения с фиксированным, но неизвестным числом.

Рассмотрим примеры

1. Сравнить : -а и 3а

Решение.

Если а < 0, то -а > 3а;

Если а=0, то -а=3а;

Если а>0, то -а<3а;

2.Решить уравнение ах = 1.

Решение.

На первый взгляд кажется возможным сразу дать ответ х = . Однако при а = 0 данное уравнение решений не имеет, и верный ответ выглядит так:

Если а = 0, то нет решений;

Если а0, то х =.

3.Решить уравнение (а² - 1)х = а + 1.

Решение.

При решении этого уравнения достаточно рассмотреть такие случаи:

а) а = 1; тогда уравнение принимает вид 0х = 2 и не имеет решений;

б) а = -1; получаем 0х = 0, и очевидно х - любое;

в) а1; имеем х = .

5.Решить неравенство .

Решение.

Ясно, что при а 0 правая часть неравенства отрицательна, и тогда при любом х левая часть больше правой. В случае, когда а = 0, важно не упустить, что исходному неравенству удовлетворяют все действительные числа, кроме х = 3.

Ответ. Если а0, то х -любое; если а = 0, то х<-3 или х>3.

II. Решить самостоятельно уравнение(с последующим разбором)

а) .

Решение.

Это уравнение равносильно системе: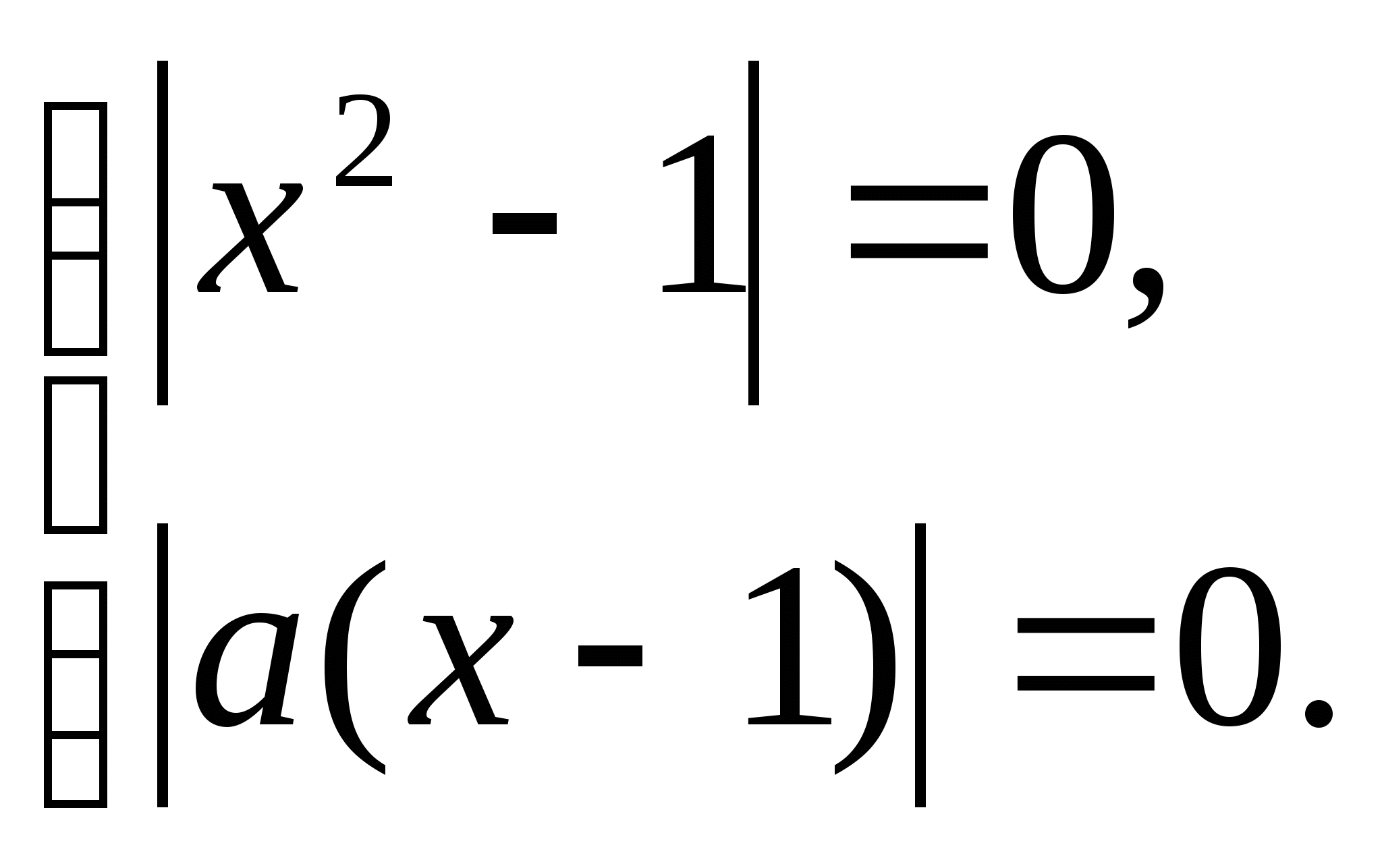

При а второе уравнение системы, а значит, и сама система, имеет единственное решение х -= 1. Если же а = 0, то из второго уравнения получаем х - любое. Следовательно, в это случае система имеет два решения х = 1 или х = -1.

Ответ. Если а0, то х = 1; если а = 0, то х =

б) Решить уравнение =0.

Решение.

х = а - единственное решение. Так как х1, то а.

Ответ. Если а, то х = а; если а = 1, то решений нет.

в) Решить неравенство

Решение.

Данное уравнение равносильно системе:

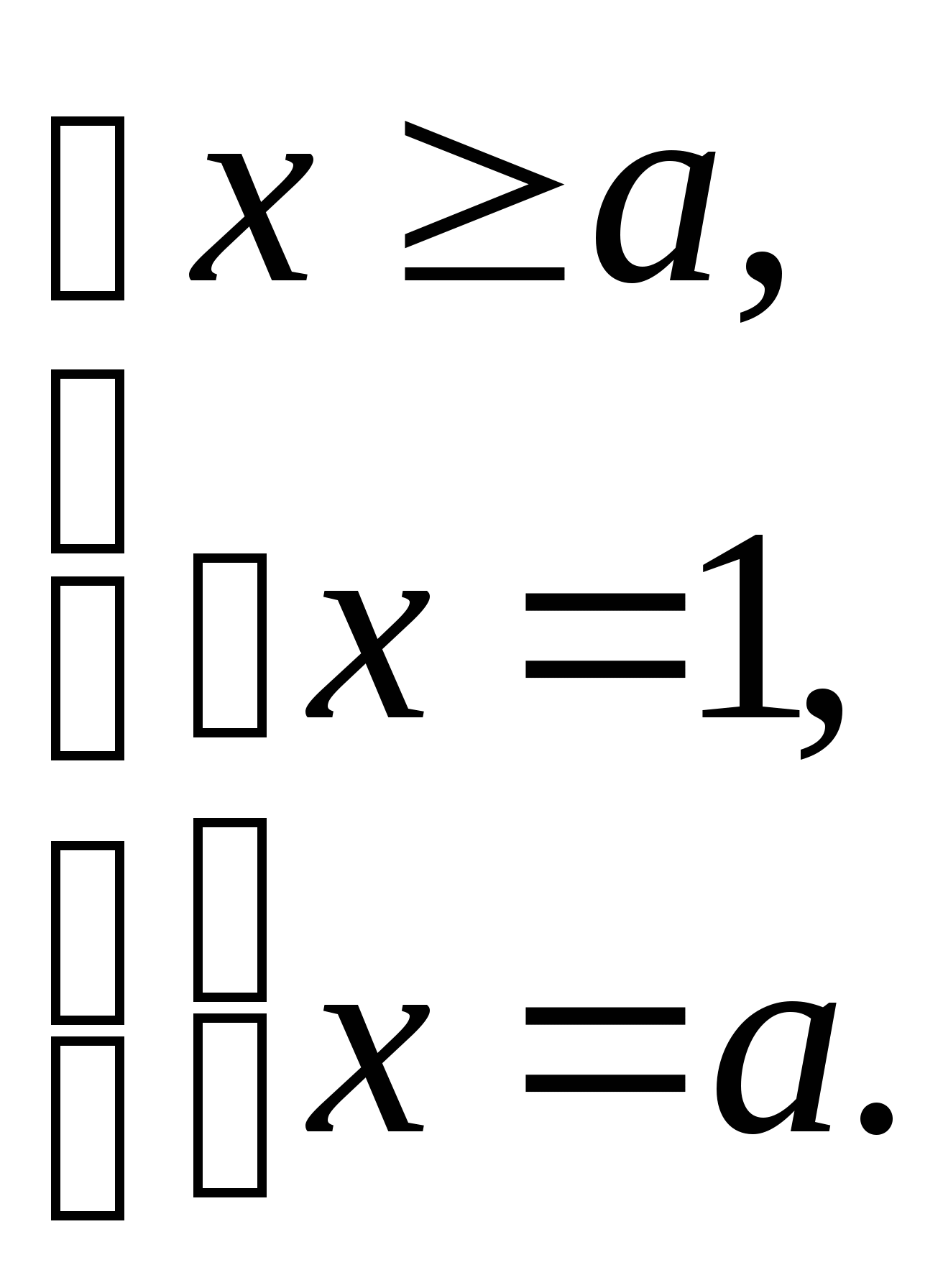
Отсюда х = а - корень исходного уравнения при а любом, а х = 1 - корень лишь при а 1.

Ответ. Если а<1, то х = а или х = 1;

Если а = 1, то х = 1; если а > 1, то х = а.

1. Итоги занятия.