Урок по алгебре и началам анализа на тему 'Сложная функция'

Департамент внутренней и кадровой политики Белгородской области

областное государственное автономное образовательное учреждение

среднего профессионального образования

«Белгородский политехнический колледж»

Методическая разработка

открытого урока

по дисциплине ОДп.10 «Математика»

Тема: «Сложная функция»

Подготовила

преподаватель математики

Съедина В.В.

Белгород - 2014

Пояснительная записка

Урок разработан для обучающихся 1 курса специальностей среднего профессионального образования, реализующих образовательные программы среднего (полного) общего образования.

Разработка может быть использована в рамках изучения раздела «Функции, их свойства и графики», а также отдельные элементы урока могут быть использованы при изучении темы «Производная сложной функции»

Разработка урока снабжена авторской презентацией, которая на всех этапах урока помогает визуализировать учебный материал, а также осуществить первичное закрепление и контроль усвоения во время объяснения нового материала, во время первичного закрепления и отработки навыков при решении задач путем «дозированной» информации, выводящейся на слайдах поэтапно.

Урок рассчитан на 1 академический час (45 минут).

Приложения к конспекту урока;

- презентация «Сложная функция»;

- индивидуальные карты-модули для учащихся.

Конспект открытого урока по математике

на тему: «Сложная функция»

Тип урока - изучение нового материала

Цели урока:

• Обучающие цели:

создать условия для формирования нового понятия «сложная функция», обеспечить развитие умения по распознаванию сложных функций, создать условия для освоения навыков построения графика сложной функции.

• Развивающие цели:

создать условия для развития познавательного интереса учащихся, развития аналитического мышления, расширения кругозора учащихся.

• Воспитательные цели:

создать условия для развития математической культуры, культуры речи, создать условия для воспитания целеустремленности, аккуратности

Целью изучения данной темы является формирование общих и профессиональных компетенций обучающихся:

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 8 Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

ПК 6.4 Контролировать ход и оценивать результаты выполнения работ

ПК 6.5 Вести утвержденную учетно - отчетную документацию

Оборудование:

• Презентация «Сложная функция»;

• Экран, проектор, доска;

• Индивидуальные карты-модули;

• Учебники:

Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. - М., 2010, Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. - М., 2009.

Структура урока:

I. Организационный момент - 0,5 мин.

II. Этап подготовки учащихся к активному сознательному усвоению знаний - 4,5 мин.

III. Этап усвоения новых знаний - 30 мин.

IV. Этап закрепления новых знаний - 8 мин.

V. Этап информирования учащихся о домашнем задании и инструктажа по его выполнению - 2 мин.

Ход занятия

I. Организационный момент

II. Этап подготовки учащихся к активному сознательному усвоению знаний

Слайд 1.

Тема нашего занятия «Сложная функция». С понятием «функция» вы уже знакомы, да и понятие «сложный» так же известен вам. Однако часто в повседневной речи мы часто считаем слова «сложный» и «трудный» синонимами. Но на самом деле «сложный» и «Трудный» далеко не всегда означают одно и то же.

В толковом словаре В.И. Даля можно найти такое определение «Сложный, составной, сложенный или составленный из разных частей…».

Наша с вами задача убедиться, что сложная функция - это не значит трудная!

Слайд 2.

Итак, цель нашего сегодняшнего занятия разобраться, что же такое «Сложная функция», как распознать сложную функцию и научиться строить график сложной функции.

Прежде чем рассматривать сложную функцию, давайте вспомним основные понятия, которые нам сегодня потребуются при изучении нового материала. Перед каждым из вас лежат индивидуальные карты, прочтите 5 вопросов, которые там приведены, подумайте и ответьте на них. У вас в распоряжении 1,5 мин.

Вводная беседа по ранее изученному материалу:

1. Что значит задать функцию?

2. Что такое аргумент функции?

3. Что такое значение функции?

4. Что называют областью определения функции?

5. Что называют областью значений функции?

Слайд 3.

Итак, еще раз обращаю ваше внимание, что функция, это прежде всего некоторое соответствие между множеством Х (независимых переменных) и множеством У (значений функции), при этом обязательно нужно помнить что каждому значению х соответствует единственное значение у.

III. Этап усвоения новых знаний

Достаточно часто мы сталкиваемся с задачами, где значение функции зависит не непосредственно от аргумента, через «промежуточную» функцию. Такие функции называют сложными

Слайд 4.

Или говорят, что «сложная функция - это композиция двух и более функций». Термин «сложная» функция не является понятием сложности начертания или исследования, а указывает на вид или «конструкцию» функциональной зависимости.

Рассмотреть слайд, обратить внимание на промежуточный шаг x₀→ t₀ →y₀.

Слайд 5.

Сложную функцию можно задать формулой y=f(g(x)), где g(x) - внутренняя функция, f(t) - внешняя функция. Обратите внимание, эта формула есть в ваших индивидуальных картах .

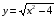
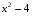Рассмотрим пример сложной функции

g(x) = - внутренняя функция, f(t) = - внешняя функция.

Для определения какая функция является внутренней, а какая внешней нужно задать вопрос: «в каком порядке будут выполнены действия при необходимости вычисления значения функции по заданному аргументу?»

Найдите y(2)-?

1) Сначала нужно найти значение подкоренного выражения 2²-4=0, то есть g(x) = x²-4 - будет внутренней функцией;

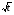2) затем уже находим значение корня 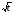=0, то есть f(t) = будет внешней функцией.

Слайд 6.

Перед вами на экране и в индивидуальных картах приведены примеры сложных функций: y = sin2x, y = (x³ - 1 )⁵ , y = cos(7x + 2), ,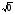

y = sin²x + sin x .

Вам необходимо определить какая функция является внутренней, а какая внешней, и заполнить таблицу. На выполнение задания вам дается 3 минуты.

Слайд 7.

Самопроверка (2 мин.). Проверьте правильность выполненного задания (около каждой функции проставьте «+» или « - » и подсчитайте количество правильных ответов).

Слайд 8.

Помимо умения различать в заданных функциях внутреннюю и внешнюю функции необходимо уметь составлять композицию функций.

На экране приведены три элементарных функции. Вам необходимо составить композицию этих функций по заданным формулам.

Например y=h(f(x))=[ f(x)=t=x² , h(t)=sin t ] =sin x²

Рассуждая аналогично, составьте, пожалуйста, композицию из функций в соответствии с заданием, на выполнение этого задания вам дается 3 минуты.

Проверка (1 мин.) - опрос по цепочке, сверка с доской (около каждой функции проставьте «+» или « - » и подсчитайте количество правильных ответов).

Слайд 9.

Итак, мы с вами рассмотрели, как в аналитически заданной функции определить внутреннюю и внешнюю функции.

Что бы еще раз убедиться, что сложная функция является композицией двух функций, построим график функции _.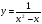

_{Фронтальная беседа (2 мин):}

_{1. Определите внутреннюю и внешнюю функции.}

_{2. Укажите область определения каждой функции}

_{3. Что можно сказать о четности этой функции.}

_{Подведение итога опроса слайд 10 .}

_{Слайд 11.}

Как мы уже говорили, сложная функция - это композиция функций. Построим графики внутренней и внешней функции в координатных осях XOG и GOУ. Для этого составим таблицы значений каждой функции. Заполните таблицы в индивидуальных картах (2 минуты).

Слайд 12.

Проверьте правильность своих вычислений, и как показано на экране, постройте графики двух функций в разных системах координат (на построение у вас - 3 минуты).

Посмотрите на экран, вот что у вас должно было получиться.

Слайд 13.

А теперь рассмотрим как, используя полученные графики, построить график сложной функции.

Возьмем некоторое х₀=0 и по первому графику найдем соответствующее ему значение g₀=-1, затем по второму графику для g₀=-1, найдем у₀=1/2 и построим в новой системе координат точку с координатами (0:1/2). Аналогично, можно построить и другие точки x₁=1 →g₁=0 →y₁=1→(1;1), учитывая четность функции, получаем точку (-1;1). И строим эскиз графика сложной функции.

Проделайте эту операцию самостоятельно в своих индивидуальных картах, для удобства можете использовать вспомогательную таблицу. На выполнение работы 5 мин. (пройти для проверки и корректировки выполнения задания, проверить выполнение заданий по определению внутренней и внешней функции, составлению сложных функций).

IV. Этап закрепления новых знаний

Используя имеющиеся графики, постройте график функции y=(2^x)²-1

(на выполнение 4 минуты) - первый справившийся учащийся на доске выполняет чертеж графика

Итак, мы рассмотрели понятие сложной функции как композицию двух функций, внешней и внутренней. Научились распознавать эти функции в конкретно заданной функции, а также составлять композицию двух функций. А также посмотрели, как с помощью графиков элементарных функций можно построить график сложной функции.

Фронтальный опрос:

1. Объясните понятие «сложная функция»

2. Как распознать внешнюю и внутреннюю функции?

3. Можно ли утверждать, что график сложной функции - это обязательно сложная кривая, для построения которой необходимы сложные вычисления и преобразования?

Хочется отметить, что слова «сложный», «сложенный» связаны с глаголом «сложить», «складывать». В словаре В.И. Даля читаем, что «СКЛАД» - это стройность, красота, порядок, устройство, а «складный ум - логичный, ясный и верный». Мне хотелось, что бы сложная функция оказалась для вас в первую очередь не трудной, а интересно устроенной.

По итогам работы на уроке выставляются отметки активным учащимся.

V. Этап информирования учащихся о домашнем задании и инструктажа по его выполнению

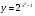В ваших индивидуальных картах записано домашнее задание: построить график функции

Построение выполнить в рабочих тетрадях.

Индивидуальные карты сдать для проверки на следующем уроке.

Спасибо за урок.

Заключение

Данная разработка была опробована на группе 1 курса с достаточно высоким уровнем подготовки, цели и задачи урока были достигнуты в полном объеме.

Использование индивидуальных карт-модулей позволило сократить время, как при объяснении нового материала, так и при закреплении, что позволило рассмотреть на уроке достаточно большой объем материала.

При изучении материала была использована презентация, в которой пошагово рассмотрены все этапы урока, что позволило увеличить плотность урока и оптимально увеличить его темп. Чередование проверки и самопроверки в ходе объяснения нового материала, позволило в ходе урока проводить коррекцию усвоения и реализовать индивидуальный подход к каждому учащемуся.

Литература

1. Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. - М., 2010.

2. Башмаков М.И. Математика (базовый уровень). 10-11 кл. - М., 2007.

3. Башмаков М.И. Математика: учебник для 10 кл. - М., 2007.

4. Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. - М., 2009.

Приложение 1.

Фамилия, имя учащегося______________________________________

Тема занятия: «Сложная функция»

Цель:

• Познакомить с понятием «сложная функция»;

• Научить распознавать сложные функции;

• Научить строить график сложной функции;

Ход занятия:

1. Ответьте на вопросы:

1. Что значит задать функцию?

2. Что такое аргумент функции?

3. Что такое значение функции?

4. Что называют областью определения функции?

5. Что называют областью значений функции?

2. Сложная функция - это композиция двух и более функций.

Формула для задания сложной функции

y=f(g(x)) - сложная функция

g(x) - внутренняя функция

f(t) - внешняя функция

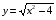
Пример.

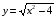
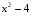g(x) = - внутренняя функция, f(t) = - внешняя функция

3. Заполните таблицу

Сложная функция

y=f(g(x))

Внешняя функция

f(t)

Внутренняя функция

g(x)

1. y = sin2x

2. y = (x³ - 1 )⁵

3. y = cos(7x + 2)

4.

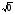
5. y = sin²x + sin x

4. Составьте сложную функцию, если f(x)=x², g(x)=2x-4, h(x)=sin x

пример: y=h(f(x))=sin x²

• y₁=f(g(x)) ____________________________________

• y₂=g(f(x)) ____________________________________

• y₃= f(h(x)) ____________________________________

• y₄=h(g(x)) _____________________________________

5. Пример. Построить график функции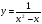

Решение

- Определим внутреннюю и внешнюю функции y=f(g(x)): g(x)=x²-1, f(g)=2^g.

- Построим на разных координатных плоскостях графики функций g(x)=x²-1и f(g)=2^g, для этого составим таблицы значений каждой функции

g(x)=x²-1 f(g)=2^g

х

-2

-1

0

1

2

g

-2

-1

0

1

2

3

g

y

Примечание 1 клетка=1 Примечание 1 клетка=0,5

Учитывая, что сложная функция есть композиция двух функций, т.е. составим вспомогательную таблицу

x

-2

-1

0

1

2

g

f

Построим график сложной функции: 1 клетка = 0,5

Задания для самостоятельной работы:

В рабочих тетрадях постройте график функции y=(2^x)²-1

Домашнее задание:

Построить график функции