Урок в 11 классе по теме 'Логарифмические уравнения'

Урок алгебры в 11 классе

Тема. Логарифмические уравнения.

Образовательная цель: формирование умений решать различные логарифмические уравнения с использованием свойств логарифмов и общих методов решения уравнений.

Развивающая цель:

• сформировать умения применять полученный алгоритм к решению уравнений.

• Формирование аналитического мышления в ходе обсуждения целесообразности применения различных методов решения уравнений.

Воспитательная цель:

• Развитие грамотной математической речи учащихся;

• сформировать умение наблюдать, подмечать закономерности, обобщать, проводить рассуждения по аналогии.

Оснащение урока: раздаточный материал и карточки-консультанты.

Ход урока.

I. Актуализация опорных знаний..

1) Учащимся предлагается печень вопросов для повторения определения логарифмической функции и ее свойств и свойств логарифмов.

1. Определение логарифма ( ^log _a ^b)

2. Основное логарифмическое тождество а ^log _a ^b = b

3. a). 5 ^log 5 ³¹; б). log b = - 3

4. Основные свойства логарифмов

1. ^log_a¹ =0

2. ^log_a^a =1

3. ^log _a ^{(x y) =log} _a ^{x + log} _a ^y

4. ^log _a 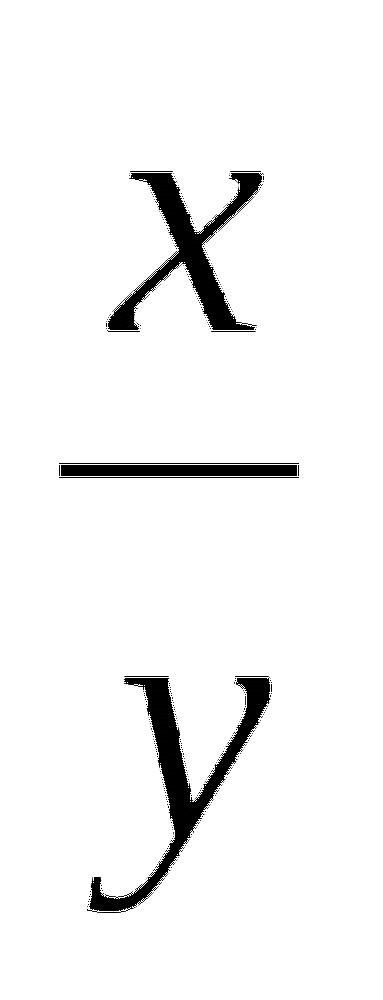^=log _a ^{x -log} _a ^y

5. ^log _a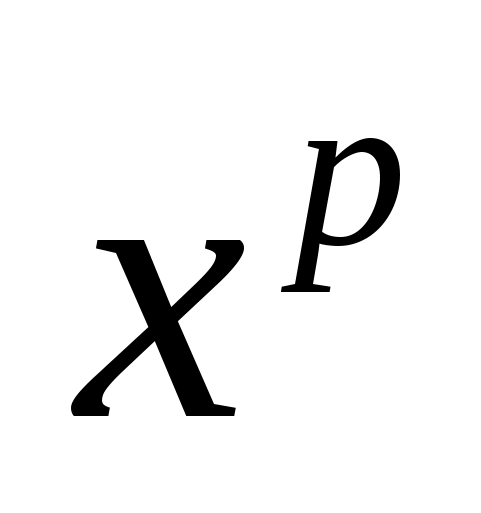=p^log _a ^b

6. ^log _a ^x =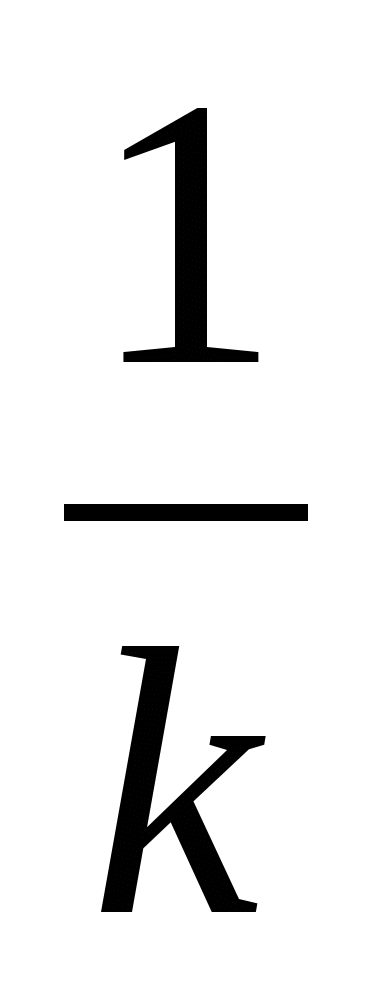^log _a ^x

7. ^log _a ^x 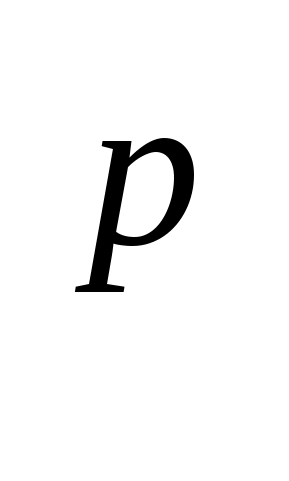=^plog _aX

5. Формула перехода к новому основанию

^log _a ^x =

6. ^log _a ^{b . log} _b ^a = 1.

Ученик у доски расшифровывает записи на карточке.

2) Задания выполняются устно (фронтально).

1. Решить уравнение:

1. 2^х = 32;

2. 2^х =0, 5; (х = -1)

3. 2^х = 7; ( 2х =2^log₂ ⁷; х= ^log ₂ ⁷).

4. 2^х = - 2;

5. 2^log₂ ⁹ = x +1(x= 8).

2. Вычислить:

1. ^log₂ ⁴⁸- ^log₂ ³(х = 4)

2. ^log₆⁴ +^log₆ 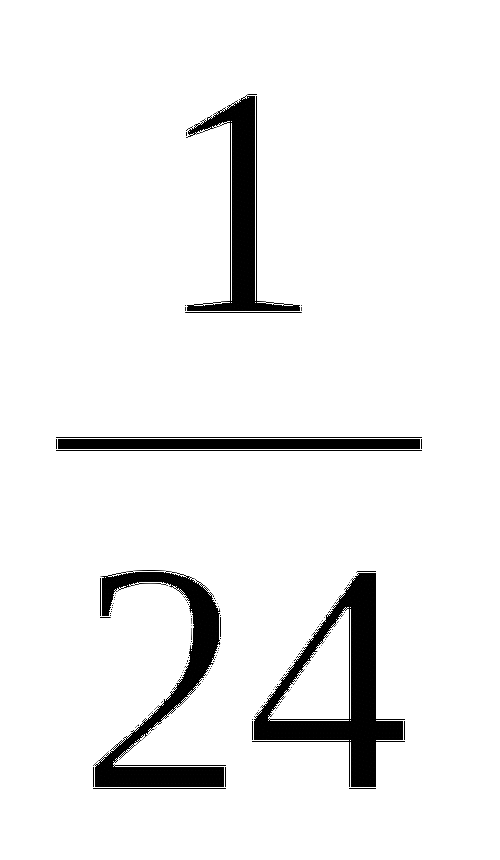(х = -1)

3. ^log₅ 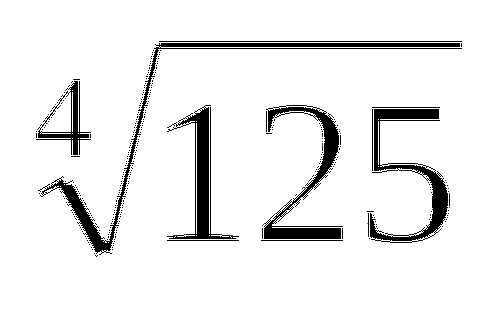(х = 3\4)

3.Решить уравнение:

1. ^{log 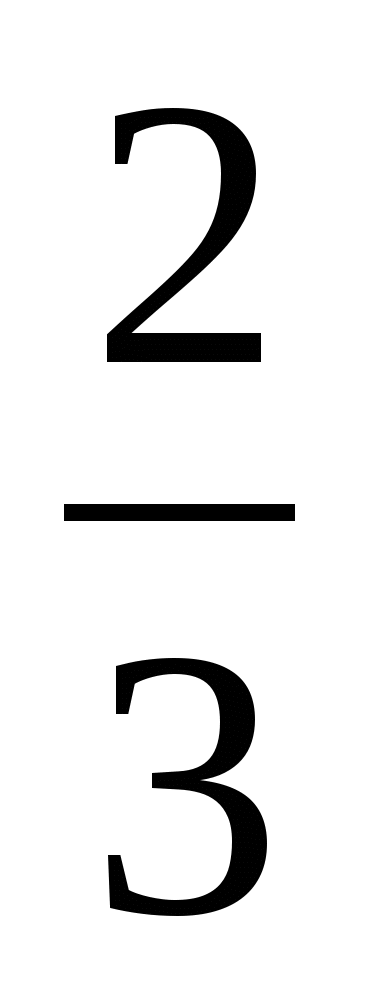x = -2 (х = 9\4})

2. ^log _х ^{9 = 2 ( х=3)}

3. ^log ₃ ^{x = log} _х ⁴

4. ^log ₈ ^log ₃ ^{x =0 (log} ₃ ^{x =1; х = 3)}

II. Мотивация к изучению темы и постановка целей урока.

Логарифмические уравнения и системы уравнений всегда есть в тестовых заданиях ЕГЭ, как в разделе А, так и в разделе В и разделе С.

Ориентирую школьников на то, что одно уравнение или система уравнений в разделе С, содержащее логарифмы, в большинстве случаев оказывается вполне решаемым даже школьниками не с самыми блестящими успехами в математике.

Школьник должен иметь четкое представление о том, что все логарифмические уравнения, какой бы степени сложности они не были, решаются по единым алгоритмам. Эти алгоритмы рассмотрим на этом уроке. Их немного: всего пять. Если их освоить, то решение уравнения с логарифмами становится посильной задачей для многих даже из раздела С.

III.Объяснение новой темы.

Школьники записывают тему урока:

«Способы решения логарифмических уравнений».

Учитель называет способ, школьники записывают его название и решают совместно с учителем соответствующими уравнения. Работа идет фронтально.

1. По определению логарифма.

^log_2+х ^{(2x+ 7) = 2}

Зададим область допустимых значений данного уравнения (ОДЗ):

2 + х 1, x - 1

2 + х > 0, x > - 2; - 3,5 -2 -1 x

2x + 7 > 0; x > - 3, 5. X ( -2; -1) ( -1; +)

Используя определение логарифма: Логарифм - это показатель степени,

(2 + х) ² = 2х +7

4 + 4х + х² - 2х - 7 =0

х² + 2х - 3 =0

его корни по теореме Виета: х₁ = -3, х₂ =1.

Число -3 не входит в ОДЗ, значит, ответ: х = 1.

2. Потенцирование (применение свойств логарифмов):

^log_а^{х + log}_а^{у = log}_а^ху

^log_а^{х - log}_а^{у = log}_а

lg x - lg (2x - 5) = lg 8 - 2 lg .

ОДЗ: х > 0 x>0,

2x - 5 >0, x>2,5,

x - 3 >0, x>3, x>3, x ( 3; + )

Применим свойства логарифма, а также формулы вынесения показателей степеней из-под логарифма

т.к. справа и слева в равенстве одинаковые десятичные логарифмы, значит, и под логарифмами выражения равны между собой.

Воспользуемся свойством пропорции:

Х (х - 3) = 2 (2х - 5)

Х² - 3х -4х + 10 = 0

Х² - 7х + 10 = 0 его корни по теореме Виета:

х₁ = 2, х₂ =5. Число 2 не входит в ОДЗ.

Ответ: 5.

3. Замена переменных.

lg³x² - lg²x³ + lg x = 0 ОДЗ: х>0,

(lg x²)³ - (lg x³)² + lg x =0

(2 lg x)³ - ( 3 lg x)³ + lg x =0

Пусть lg x = t.

8t³ - 9 t² + t =0

t (8t² - 9 t + 1) =0

t=0 или 8t² - 9 t + t =0

D = 81 - 32 = 49

t = ; t₁ = 1; t₂ = .

Вернемся к замене: lg x =0 lg x =1 lg x =

X= 1 x= 10 x=

х₁ = 1 , х₂ =10, х₃ = .

Все три корня входят в ОДЗ.

Ответ: 1; ;10.

4. Логарифмирование обеих частей уравнения:

0, 01 ^. х ^{l g х+3} = 3 ОДЗ: х >0.

Умножим обе части уравнения на 100, чтобы убрать коэффициент при х, поскольку это сразу упростит внешний вид уравнения:

х ^{l g х+3} = 10000. Прологарифмируем обе части уравнения по основанию 10:

l g (х ^{lg х+3}) = lg 10000

( lg X + 3) lg x = 4

lg² x + 3lg x - 4 =0

Пусть lg x =t, тогда t² + 3t - 4 =0 его корни по теореме Виета

t₁ = 1; t₂ = - 4.

Вернемся к замене:

Lg x = - 4 lg x = 1

Х = 10 ^{- 4} х = 10 ¹

Х = 0, 0001 х = 10.

Оба корня входят в ОДЗ.

Ответ: 0, 0001; 10.

5. Приведение к одному основанию.

^log ₃ ^{x _ log x + log x = 5} ОДЗ: х >0

^log ₃ ^{x _ log x + log x = 5}

^log ₃ ^{x _ 2 log} ₃ ^{x + log} ₃ ^{x = 5}

^{-2 log} ₃ ^{x = 5}

^log ₃ ^{x = -}

x =

IV. Формирование знаний и умений учащихся.

После разбора этих способов решения логарифмических уравнений школьникам предлагается задание в виде карточки, с тем, чтобы школьники по своему выбору решали их, определяя способ решения с опорой на тетрадь.

Сильным учащимся предлагается карточка с ответами для индивидуализации их работы.

1. ^log_{x - 1} ^{(2x 2 -7x +7) = 2 (3)}

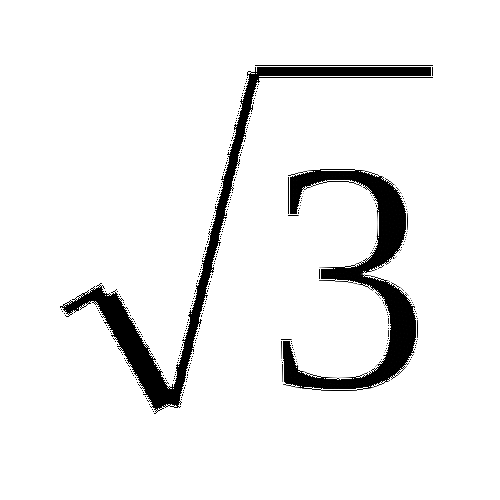
2. ^log ₂ ^{(x +14) + log = 6 (2)}

3. ^log ₈ ^{+ 2 log} ₄ ^{x + log} ₂ ^{= 11 (64)}

4. _x ^{3 - lg x} _{= 100 (x = 10, 1/ 10)/}

V.Итог урока.

В результате изучения данной темы вы познакомились с основными способами решения логарифмических уравнений на основе ранее изученного материала. Еще раз мы убедились в практической значимости теоретических знаний алгебры.

VI.Задание на дом.

п.39, №514 (а, б), №518 (а, б), №523 (а, б).