- Учителю
- Рабочая программа по алгебре для 7 класса
Рабочая программа по алгебре для 7 класса
Муниципальное бюджетное образовательное учреждение
«Кяхтинская средняя общеобразовательная школа № 1»
671843, Республика Бурятия, г. Кяхта, ул. Рукавишникова, 6
тел. 8(30142) 91963
«Рассмотрено»
Заседание МО
Протокол № _____
от______________ 2013 г. Руководитель МО_________
подпись
________________________
ФИО
«Согласовано»
Заместитель директора по НМР МБОУ «КСОШ №1»
_________ /Суровцева С.В./
Дата «___»_________2013г.
«Утверждаю»
Директор школы
___________/Максимов Л.А/
Приказ № ______________
от______________ 2013 г.
Рабочая программа
«Алгебра»
7 класс
Разработана:
В.Н. Гармаевой
учителем математики
1 квалификационная категория
Кяхта
2013г.
Пояснительная записка
Рабочая программа по математике для 7 класса составлена на основе Федерального компонента государственного стандарта среднего (полного) общего образования. Федеральный базисный учебный план для общеобразовательных учреждений РФ отводит для обязательного изучения на базовом уровне в по алгебре 123 часов (5 часов в неделю в 1-ой четверти, 3 часа в неделю во 2-4 четверти).
Рабочая программа разрабатывалась на основе принятой основной образовательной программы учебного плана МБОУ КСОШ №1; примерных учебных программ; учебного курса по математике, рекомендованных министерством образования и науки РФ. На основании требований Государственного образовательного стандарта 2004 г. в содержании календарно-тематического планирования предусмотрено формирование у школьников общеучебных умений и навыков, универсальных способов деятельности и ключевых компетенций. Реализация программы обеспечивается нормативными документами:
-
Федеральным компонентом государственного стандарта общего образования (приказ МОиН РФ от 05.03.2004 №1089) и Федеральным БУП для общеобразовательных учреждений РФ (приказ МО РФ от 09.03.2004 №1312);
Для реализации учебной программы используется учебно-методический комплект, включающий:
1.Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова. Алгебра. Учебник для 7 класса общеобразовательных учреждений. - М.: Просвещение, 2009 г. - 240 с.
Актуальность программы
Программа обеспечивает достижения планируемых результатов освоения основной образовательной программы общего среднего образования.
Для изучения курса рекомендуется классно-урочная система с использованием различных технологий, форм, методов обучения. Программа конкретизирует содержание предметных тем, предлагает распределение предметных часов по разделам курса, последовательность изучения тем и разделов с учетом меж предметных и внутри предметных связей, логики учебного процесса, возрастных особенностей учащихся. Определен также перечень кимов. Изменения внесены с учётом особенностей организации, формирования разновозрастных и разноуровневых объединений детей, нестандартностью индивидуальных результатов обучения и воспитания. Программа обеспечивает оптимальную нагрузку на ребёнка с целью защиты его от переутомления.
Рабочая программа предусматривает выполнение практической части курса: 10 контрольных работ.
Общая характеристика учебного предмета
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Алгебра Изучение алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности - умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
В курсе алгебры 7 класса систематизируются и обобщаются сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной; учащиеся знакомятся с важнейшими функциональными понятиями и с графиками прямой пропорциональности и линейной функции общего вида, действиями над степенями с натуральными показателями, формулами сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители, со способами решения систем линейных уравнений с двумя переменными, вырабатывается умение решать системы уравнений и применять их при решении текстовых задач.
ОСНОВНОЕ СОДЕРЖАНИЕ (алгебра).
Выражения, тождества, уравнения (20 часов)
Числовые выражения с переменными. Простейшие преобразования выражений. Уравнение, корень уравнения. Линейное уравнение с одной переменной. Решение текстовых задач методом составления уравнений.
Статистические характеристики.
Функции (13 часов)
Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и её график.
Степень с натуральным показателем (13часов)
Степень с натуральным показателем и ее свойства. Одночлен. Функции у=х2, у=х3 и их графики.
Многочлены (19 час)
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочленов на множители.
Формулы сокращенного умножения (21 час)
Формулы (а - b )(а + b ) = а2 - b 2, (а ± b)2 = а2± 2а b + b2, (а ± b)3 = а3 ± За2b + За b2 ± b3, (а ± b) (а2 ![]() а b + b2) = а3 ± b3. Применение формул сокращённого умножения в преобразованиях выражений.
а b + b2) = а3 ± b3. Применение формул сокращённого умножения в преобразованиях выражений.
Системы линейных уравнений (16часов)
Система уравнений. Решение системы двух линейных уравнений с двумя переменными и его геометрическая интерпретация. Решение текстовых задач методом составления систем уравнений.
Повторение (18 часов) и в начале года 3 часа.
Требования к уровню подготовки обучающихся в 7 классе
В ходе преподавания алгебры в 7 классе, работы над формированием у обучающихся перечисленных в программе знаний и умений следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
В результате изучения курса алгебры 7 класса обучающиеся должны:
знать/понимать
-
существо понятия математического доказательства; примеры доказательств;
-
существо понятия алгоритма; примеры алгоритмов;
-
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
-
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
-
как потребности практики привели математическую науку к необходимости расширения понятия числа;
-
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
-
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
-
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
Алгебра
уметь
-
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
-
выполнять основные действия со степенями с натуральными показателями, с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
-
решать линейные уравнения решать линейные решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
-
изображать числа точками на координатной прямой;
-
определять координаты точки плоскости, строить точки с заданными координатами;
-
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
-
применять графические представления при решении уравнений, систем, неравенств;
-
описывать свойства изученных функций (у=кх, где к
 0, у=кх+b, у=х2, у=х3), строить их графики.
0, у=кх+b, у=х2, у=х3), строить их графики.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
-
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
-
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
-
интерпретации графиков реальных зависимостей между величинами.
Элементы логики, комбинаторики,
статистики и теории вероятностей
уметь
-
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
выстраивания аргументации при доказательстве (в форме монолога и диалога);
-
распознавания логически некорректных рассуждений;
-
записи математических утверждений, доказательств;
-
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
-
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
-
понимания статистических утверждений.
Литература для учителя
-
Я иду на урок математики: 7 класс: Книга для учителя. - М.: Издательство «1 сентября», 2000;
-
Алгебра. 7 класс: поурочные планы по учебнику Ю.Н. Макарычева и др. / авт.-сост. Л.А Топилина, Т.Л. Афанасьева. - Волгоград: Учитель, 2006;
-
Математика 5-11 классы: нетрадиционные формы организации контроля на уроках / авт.-сост. М.Е. Козина, О.М. Фадеева. - Волгоград, Учитель, 2007;
-
В.И.Жохов, Л.Б.Крайнева Уроки алгебры в 7 классе- М.: «Вербум - М», 2000;
-
Н.П.Кострикина Задачи повышенной трудности в курсе алгебры 7-9 классов - М : Просвещение», 1991;
-
Нестандартные уроки алгебры. 8 класс. Сост. Ким Н.А. - Волгоград: ИТД «Корифей», 2006;
-
Математика 5-11 классы: нетрадиционные формы организации контроля на уроках / авт.-сост. М.Е. Козина, О.М. Фадеева. - Волгоград, Учитель, 2007;
-
Конструирование современного урока математики: кн. для учителя / С.Г. Манвелов. - М.: Просвещение,2005.
Список контрольных работ
Алгебра 7 класс
№
Тема
1
Контрольная работа №1 ««Выражения. Тождества»
2
Контрольная работа №2 «Уравнение с одной переменной»
3
Контрольная работа по теме №3 «Линейная функция»
4
Контрольная работа № 4 «Степень с натуральным показателем»
5
Контрольная работа № 5 по теме: «Сложение и вычитание многочленов»
6
Контрольная работа №6 «Умножение многочленов»
7
Контрольная работа №7 «Формулы сокращенного умножения»
8
Контрольная работа № 8 «Преобразование целых выражений»,
9
Контрольная работа №9 «Системы линейных уравнений »
10
Итоговая контрольная работа
Формы и средства контроля.
Основными методами проверки знаний и умений учащихся по алгебре являются письменные работы. К письменным формам контроля относятся: математические диктанты, самостоятельные и контрольные работы, тесты. Основные виды проверки знаний - текущая и итоговая. Текущая проверка проводится систематически из урока в урок, а итоговая - по завершении темы (раздела), школьного курса. Ниже приведены контрольные работы для проверки уровня сформированности знаний и умений учащихся после изучения каждой темы и всего курса в целом.
Контрольные работы по алгебре 7 класс.
Контрольная работа №1 «Выражения и тождества»
ВАРИАНТ 1
1. Найдите значение выражения: ![]() .
.
2. Упростите выражение:
а) 5a - 3b - 8a + 12b;
б) 16с + (3с - 2) - (5с + 7);
в) 7 - 3(6у - 4).
3. Сравните значения выражений 0,5х - 4 и 0,6х - 3
при х = 5.
4. Упростите выражение 6,3х - 4 - 3(7,2х + 0,3) и найдите его значение при ![]() .
.
5.В прямоугольном листе жести со сторонами х см и у см вырезали квадратное отверстие со стороной 5 см.
а) Найдите площадь оставшейся части.
б) Решите задачу при х = 13, у = 22.
ВАРИАНТ 2
1. Найдите значение выражения: ![]() .
.
2. Упростите выражение:
а) 3х + 7у - 6х - 4у;
б) 8а + (5 - а) - (7 + 11а);
в) 4 - 5(3с + 8).
3. Сравните значения выражений 3 - 0,2а и 5 - 0,3а
при а = 16.
4. Упростите выражение 3,2а - 7 - 7(2,1а - 0,3) и найдите его значение при ![]() .
.
5.В кинотеатре п рядов по т мест в каждом. На дневной сеанс были проданы билеты на первые 7 рядов.
а) Сколько незаполненных мест было во время сеанса?
б) Решите задачу при п = 21, т = 35.
Контрольная работа №2 «Уравнение с одной переменной»
ВАРИАНТ 1
Решите уравнение:
а) ![]() ;
;
б) 11,2 - 4х = 0;
в) 1,6(5х - 1) = 1,8х - 4,7.
2. При каком значении переменной значение выражения 3 - 2с на 4 меньше значения выражения 5с + 1?
3. Турист проехал в 7 раз большее расстояние, чем прошёл пешком. Весь путь туриста составил 24 км. Какое расстояние турист проехал?
4.Длина прямоугольника на 6 см больше ширины. Найдите площадь прямоугольника, если его периметр равен 48 см.
ВАРИАНТ 2
1. Решите уравнение:
а) ![]() ;
;
б) 9х + 72,9 = 0;
в) 2(0,6х + 1,85) - 0,7 = 1,3х.
2. При каком значении переменной значение выражения 4а + 8 на 3 больше значения выражения 3 - 2а?
3. На одной полке на 15 книг больше, чем на другой. Всего на полках 53 книги. Сколько книг на каждой полке?
4.Ширина прямоугольника в 2 раза меньше длины. Найдите площадь прямоугольника, если его периметр равен 120 м.
Контрольная работа №3 «Линейная функция»
ВАРИАНТ 1
1. Функция задана формулой у = х - 7. Найдите:
а) значение функции, соответствующее значению аргумента, равному 4;
б) значение аргумента, при котором значение функции равно -8.
2. а) Постройте график функции у = 3х - 4.
б) С помощью графика найдите значение функции, соответствующее значению аргумента 2,5.
3. В одной системе координат постройте графики функций:
а) у = -0,5х; б) у = 2.
4. Проходит ли график функции у = -5х + 11 через точку:
а) М(6; -41); б) N(-5; 36) ?
5.Каково взаимное расположение графиков функций
у = 15х - 51 и у = -15х + 39? В случае пересечения графиков найдите координаты точки их пересечения.
ВАРИАНТ 2
. Функция задана формулой у = 5 - х. Найдите:
а) значение функции, соответствующее значению аргумента, равному 6;
б) значение аргумента, при котором значение функции равно -1.
2. а) Постройте график функции у = -2х + 5.
б) С помощью графика найдите значение функции, соответствующее значению аргумента -0,5.
3. В одной системе координат постройте графики функций:
а) у = 3х; б) у = -5.
4. Проходит ли график функции у = -7х - 3 через точку:
а) С(-8; -53); б) D(4; -25) ?
5.Каково взаимное расположение графиков функций
у = -21х - 15 и у = 21х + 69? В случае пересечения графиков найдите координаты точки их пересечения.
Контрольная работа №4 «Степень с натуральным показателем»
ВАРИАНТ 1
1. Выполните действия:
а) х5 х11; б) х15 : х3; в) (х4)7; г) (3х6)3.
2. Упростите выражение:
а) 4b2с (-2,5bс4); б) (-2x10у6)4.
3. Постройте график функции у = х2. С его помощью определите:
а) значение функции, при значении аргумента, равному -1,5;
б) значения аргумента, при которых значение функции равно 3.
4. Найдите значение выражения:
а) ; б) 3х3 - 1 при х = - .
5.Упростите выражение ![]() .
.
ВАРИАНТ 2
1. Выполните действия:
а) а9 а13; б) а18 : а6; в) (а7)4; г) (2а3)5.
2. Упростите выражение:
а) -7х5у3 1,5ху; б) (-3т4п13)3.
3. Постройте график функции у = х2. С его помощью определите:
а) значение функции, при значении аргумента, равному 2,5;
б) значения аргумента, при которых значение функции равно 5.
4. Найдите значение выражения:
а) ; б) 2 - 7х2 при х = - .
5.Упростите выражение ![]() .
.
Контрольная работа №5 «Сложение и вычитание многочленов»
ВАРИАНТ 1
1. Упростите выражение:
а) (7х2 - 5х + 3) - (5х2 - 4); б) 5а2 (2а - а4).
2. Решите уравнение 30 + 5(3х - 1) = 35х - 15.
3. Вынесите общий множитель за скобки:
а) 7ха - 7хb; б) 16ху2 + 12х2у.
4. По плану тракторная бригада должна была вспахать поле за 14 дней. Бригада вспахивала ежедневно на 5 га больше, чем намечалось по плану, и потому закончила пахоту за 12 дней. Сколько гектаров было вспахано?
5. Решите уравнение:
а) ![]() ; б) х2 + х = 0.
; б) х2 + х = 0.
ВАРИАНТ 2
Упростите выражение:
а) (3у2 - 3у + 1) - (4у - 2); б) 4b3(3b2 + b).
2. Решите уравнение 10х - 5 = 2(8х + 3) - 5х.
3. Вынесите общий множитель за скобки:
а) 8аb + 4а; б) 18ab3 - 9a2b.
4. Заказ по выпуску машин должен быть выполнен по плану за 20 дней. Но завод выпускал ежедневно по 2 машины сверх плана и поэтому выполнил заказ за 18 дней. Сколько машин должен был выпускать завод ежедневно по плану?
5. Решите уравнение:
а) ![]() ; б) 2х2 - х = 0.
; б) 2х2 - х = 0.
Контрольная работа №6 «Умножение многочленов»
ВАРИАНТ 1
1.Представьте в виде многочлена:
а) (у - 4)(у + 5); в) (х - 3)(х2 + 2х - 6).
б) (3а + 2b)(5а - b);
2. Разложите на множители:
а) b(b + 1) - 3(b + 1); б) ca - cb + 2a - 2b.
3. Упростите выражение (а2 - b2)(2a + b) - аb(а + b).
4. Докажите тождество (х - 3)(х + 4) = х(х + 1) - 12.
5. Ширина прямоугольника вдвое меньше его длины. Если ширину увеличить на 3 см, а длину на 2 см, то площадь его увеличится на 78 см2. Найдите длину и ширину прямоугольника.
ВАРИАНТ 2
1. Представьте в виде многочлена:
а) (х + 7)(х - 2); в) (y + 5)(y2 - 3у + 8).
б) (4с - d)(6c + 3d);
2. Разложите на множители:
а) у(а - b) + 2(а - b); б) 3х - 3у + ах - ау.
3. Упростите выражение ху(х + у) - (х2 + у2)(х - 2у).
4. Докажите тождество а(а - 2) - 8 = (а + 2)(а - 4).
5. Длина прямоугольника на 12 дм больше его ширины. Если длину увеличить на 3 дм, а ширину - на 2 дм, то площадь его увеличится на 80 дм2. Найдите длину и ширину прямоугольника.
Контрольная работа №7 «Формулы сокращенного умножения»
ВАРИАНТ 1
1. Преобразуйте в многочлен:
а) (а - 3)2; в) (4а - b)(4а + b);
б) (2у + 5)2; г) (х2 + 1)(х2 - 1).
2. Разложите на множители:
а) с2 - 0,25; б) х2 - 8х + 16.
3. Найдите значение выражения (х + 4)2 - (х - 2)(х + 2)
при х = 0,125.
4. Выполните действия:
а) 2(3х - 2у)(3х + 2у); в) (а - 5)2 - (а + 5)2.
б) (а 3 + b 2) 2;
5. Решите уравнение:
а) (2х - 5)2 - (2х - 3)(2х + 3) = 0; б) 9у2 - 25 = 0.
ВАРИАНТ 2
. Преобразуйте в многочлен:
а) (х + 4)2; в) (2у + 5)(2у - 5);
б) (3b - с)2; г) (у 2 - х)(у 2 + х).
2. Разложите на множители:
а) - а2; б) b2 + 10b + 25.
3. Найдите значение выражения (а - 2b)2 + 4b(а - b) при а = - .
4. Выполните действия:
а) 3(1 + 2ху)(1 - 2ху); в) (а + b)2 - (а - b)2.
б) (х 2 - у 3) 2;
5. Решите уравнение:
а) (4х - 3)(4х + 3) - (4x - 1)2 = 3x; б) 16с2 - 49 = 0.
Контрольная работа 8 «Преобразования целых выражений»
ВАРИАНТ 1
1. Преобразуйте в многочлен:
а) (а - 2)(а + 2) - 2а(5 - а); в) 3(х - 4)2 - 3х2.
б) (у - 9)2 - 3у(у + 1);
2. Разложите на множители:
а) 25х - х3; б) 2х2 - 20х + 50.
3. Упростите выражение (с2 - b)2 - (с2 - 1)(с2 + 1) + 2bс2
и найдите его значение при b = - 3.
4. Представьте в виде произведения:
а) (х - 4)2 - 25х2; б) а2 - b2 - 4b - 4а.
5. Докажите тождество (а + b)2 - (а - b)2 = 4аb.
ВАРИАНТ 2
1. Преобразуйте в многочлен:
а) 4х(2х - 1) - (х - 3)(х + 3); в) 7(а + b)2 - 14аb.
б) (р + 3)(р - 11) + (р + 6)2;
2. Разложите на множители:
а) у3 - 49у; б) -3а2 - 6ab - 3b2.
3. Упростите выражение (а - l)2(a + 1) + (а + 1)(а - 1) и найдите его значение при а = - 3.
4. Представьте в виде произведения:
а) (у - 6)2 - 9у2; б) с2 - d 2 - с + d.
5. Докажите тождество (х - у)2 + (х + у)2 = 2(х 2 + у 2).
Контрольная работа №9 «Системы линейных уравнений»
ВАРИАНТ 1
1. Решите систему уравнений 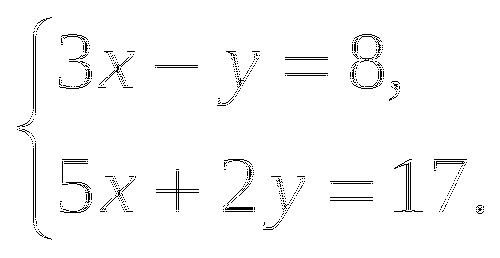
2. Студент получил стипендию 100 рублей монетами достоинством 5 рублей и 2 рубля, всего 32 монеты. Сколько было выдано монет каждого номинала?
3. Решите систему уравнений 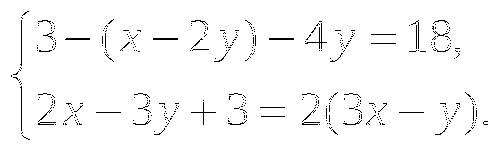
4. Постройте график уравнения 4х - 3у = 12.
5. Имеет ли решения система 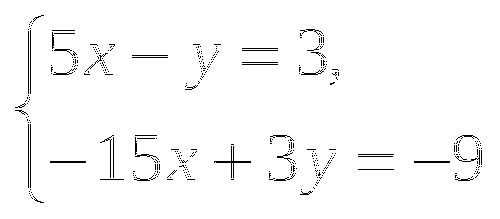 и сколько?
и сколько?
ВАРИАНТ 2
1. Решите систему уравнений 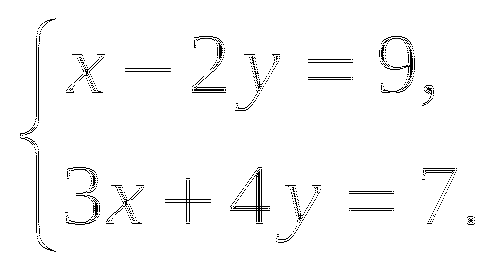
2. Кассир разменял 500-рублевую купюру на 50-рублевые и 10-рублевые, всего 22 купюры. Сколько было выдано кассиром 50-рублевых и 10-рублевых купюр?
3. Решите систему уравнений 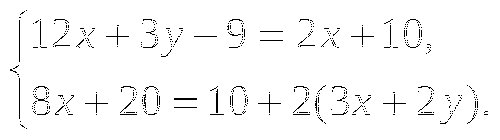
4. Постройте график уравнения 6у - 7х = 42.
5.Имеет ли решения система 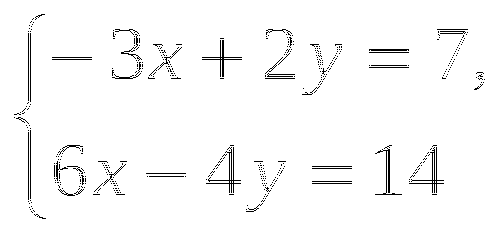 и сколько?
и сколько?
Итоговая контрольная работа
ВАРИАНТ 1
1. Упростите выражение:
![]()
2. Разложите на множители:
![]()
3. Решите равнение ![]() .
.
4. Одно полотно разрезали на 5 равных частей, а другое, длина которого на 10 м больше, на 7 таких же частей. Какова длина каждого полотна?
5. Постройте график функции ![]() и найдите координаты точки пересечения этого графика с прямой
и найдите координаты точки пересечения этого графика с прямой ![]() .
.
ВАРИАНТ 2
1. Упростите выражение:
![]()
2. Разложите на множители:
![]()
3. Решите равнение ![]() .
.
-
Муку рассыпали в 8 одинаковых по весу пакетов, а сахар - в 6 таких же пакетов. Сколько весит мука и сколько весит сахар, если сахара было на 10 кг меньше?
5. Постройте график функции ![]() и найдите координаты точки пересечения этого графика с прямой
и найдите координаты точки пересечения этого графика с прямой ![]() .
.