Уроки обощения и систематизации знаний по алгебре для 8 класса по теме «Квадратные уравнения»

Урок обобщения и систематизации знаний по теме «Квадратные уравнения».

Что может быть лучшего? Сравнив прошедшее,

свести его с настоящим!»

К.Прутков

Мотивационная беседа.

Сядьте удобнее. Пожелаем, друг другу успехов и начнём урок. Вы видите, что на доске не записана тема урока. Попробуем определить её вместе. Для этого устно выполним следующее задание:

Какое из записанных уравнений является лишним и почему?

х² - 2х + 8 = 0

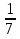- х² - 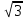х +13 = 0

х³ - 25 = 0

(х - 1)² = 0

0,6 х² +12 = 0

Х² - 64 = 0

Х² - 6х = 0

Как можно, одним словом определить вид остальных уравнений?

Значит, сегодня мы будем обобщать и систематизировать знания по теме «Квадратные уравнения». Вначале быстро повторим теорию (используется презентация). Сегодня нам предстоит вспомнить разные способы решения квадратных уравнений. За каждое верно выполненное задание вы будете получать по одному баллу. В конце урока подведём итог работы:

4 балла - «3» , ниже 4 баллов - тема плохо усвоена, необходимо её доработать,

5 баллов - «4» , 6 или 7 баллов - «5».

В ходе урока каждый ученик самостоятельно заполняет карту диагностики знаний по теме.

Решение квадратных уравнений

неполных

полных

ах²+ вх = 0 (с = 0)

Использование формулы корней

(через Д)

ах² + с = 0 ( в = 0)

Применение формулы корней чётного

второго коэффициента

ах² = 0 ( в = 0, с=0)

Применение теоремы Виета

Выделение квадрата двучлена

Графический способ

Набрано баллов

Оценка

На доске записано квадратное уравнение х² - 2х - 8 = 0

Какое это уравнение? (полное квадратное, приведённое). Составьте из данного уравнения 3 вида неполных квадратных уравнений, ориентируясь на диагностическую таблицу, и решите их:

1). х² - 2х = 0

х₁₌ 0, х₂ = 2

2). х² - 8 = 0

х₁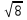₌ - , х₂ =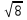

3). х² = 0

х= 0

Решение уравнений проверяется на слайдах презентации. Ученики выставляют баллы в таблицу диагностики.

Далее предлагается работа в парах. Необходимо решить данное полное уравнение возможно большим числом способов. Дети в парах могут решать уравнение либо одинаковым способом, либо разными способами. Каждый должен разобраться в решении, которое записано в тетради.

1 способ.

х² - 2х - 8 = 0

Д = в²- 4ас Д = (- 2)² - 4* ( - 8) = 36

Д>0, уравнение имеет два корня

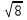
х₁ = - 2 х₂ = 4

2 способ.

По теореме Виета: х_{1 ∙} х_{2 =} - 8,

х_{1 +} х₂ = 2.

3 способ.

Выделение квадрата двучлена:

х² - 2х - 8 = 0

х² - 2х + 1 - 9 = 0

(х - 1)² = 9

х - 1 = - 3 или х - 1 = 3

х = - 2 х = 4

4 способ.

При графическом способе решения можно построить графики функций

у = х² и у = 2х + 8 и найти абсциссы их точек пересечения. Для помощи учащимся можно заранее выполнить чертежи координатной плоскости и таблиц. Это позволит значительно сэкономить время при выполнении задания. Использован шаблон координатной плоскости учителя Савченко Е.

5 способ.

Применение формулы корней для второго чётного коэффициента.

х² - 2х - 8 = 0

Д₁ =( ) ²- ас Д₁ = (- 1)² - 1∙( - 8) = 9

Д₁ > 0, уравнение имеет два корня

х =

х₁ = - 2 х₂ = 4

Вывод: при любом способе решения ответ остаётся неизменным. Поэтому так важно знать разные способы решения квадратного уравнения для проверки правильности ответа.

Гимнастика для глаз или физкультминутка.

Применение квадратных уравнений (творческое задание).

Работа в группах. Подумать над аналогичной задачей можно предложить учащимся дома.

Придумайте задачу, по условию которой можно составить квадратное уравнение

х∙ (х - 1) = 12

Какой ответ имеет уравнение? Может быть, кто-то сразу (без решения) определит его корни?

Ученики зачитывают составленные задачи. Например: ширина прямоугольного участка земли 12 м ². Известно, что ширина меньше длины на 1 метр. Найти стороны участка.

Как вы думаете, можно ли будет использовать данное уравнение при решении комбинаторной задачи:

В конце учебного года дети сфотографировались на память. Каждый подарил своим друзьям по одной фотографии. Определите количество друзей, если всего было сделано 12 фотографий.

Ответ: 4 друга по 3 фотографии.

Занимательный момент урока.

Определим лучшего ученика сегодняшнего урока. Им будет тот, кто быстрее всех сможет устно выполнить следующее задание:

Определить р и х₂ в квадратном уравнении х² - рх + 15 = 0, если х₁ = 3

Найденное значение х₂ укажет номер кабинета , р - номер парты, считая от окна, где лежит приз.

Рефлексия. Подведение итогов урока. Выставление оценок.

Возвращаемся к эпиграфу урока. Как вы понимаете слова К. Пруткова применительно к нашему уроку? Полезен ли был урок?

В качестве домашнего задания ученикам на дополнительную оценку можно предложить подумать над решением уравнения х² - 2х - 8 = 0 способом группировки.

Решение:

х² - 2х - 4 - 4 = 0

(х² - 4) + ( - 2х - 4) = 0

(х - 2)∙(х + 2) - 2 ∙( х + 2) = 0

( х + 2) ∙ ( х - 4) = 0

х = - 2 или х = 4

Выбрать квадратное уравнение из учебника алгебры и решить его несколькими способами.