- Учителю
- Разработка урока в 8 классе «Квадратичная функция и её график»
Разработка урока в 8 классе «Квадратичная функция и её график»
Квадратичная функция и её график.
Цель: - а) повторить график квадратичной функции;
б) научить переходу от графического способа задания функции к аналитическому;
в) повторить формулы сокращённого умножения;
- развить внимание, память;
- воспитать прилежное отношение к учебному труду.
Структура урока.
I . Оргмомент.
II. Проверка д/з.
III. Актуализация опорных знаний.
IV. Изложение нового материала.
V. Закрепление нового в ходе решения упражнений.
VI. Первичная проверка усвоения.
VII. Постановка д/з.
VIII. Итоги урока.
ХОД УРОКА.
Этапы урока.
Основное содержание учебного материала
Деятельность
учителя
Деятельность учеников
Время
I . Оргмомент.
Инсерт.
После проверки готовности класса к уроку сообщает тему, цели и план
Стоя приветствуют учителя, определяют цели и формулируют тему
2 мин.
II. Проверка д/з.
-
Как называется график функции у=ах² при любом а≠0 ?
-
Перечислите основные свойства функции у=ах², где а≠0.
Задаёт вопросы
Отвечают на вопросы учителя
3 мин.
III. Актуализация опорных знаний.
Построить график квадратичной функции y=x².
График квадратичной функции - парабола.
Способы задания функции.
-
аналитический
-
табличный
-
графический
Задаёт вопросы
Отвечают на вопросы учителя
5 мин.
IV. Изложение нового материала.
Сегодня мы будем учиться переходу от графического способа задания функции к аналитическому*
Объясняет у доски
Записывают, отвечают на вопросы
10 мин.
V. Закрепление нового в ходе решения упражнений.
**
Управляет работой учащихся
Решают упражнения
8 мин.
VI. Первичная проверка усвоения.
Проверочная работа по карточкам***
Выполняют работу на листах контроля
8 мин.
VII. Постановка д/з.
Построить графики функций
а)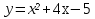
;
б)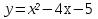
;
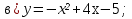
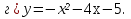
Даёт пояснения по домашнему заданию
Записывают д/з
2 мин.
VIII. Итоги урока.
Подводит итоги урока
Подводят итоги урока
2 мин.
Приём «Инсерт»
1.Прочитать текст. Напротив предложений, содержащих известную вам информацию, поставьте «+», напротив предложений, где содержится информация, требующая уточнения, - «-», предложения, содержащие неизвестную информацию, отметьте «?».
Графиком квадратичной функции является парабола.
В частности, графиком функции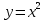 
является парабола с вершиной в точке (0;0); ось симметрии параболы - ось ординат.
В общем случае вершиной параболы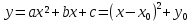 
является точка (
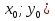, где 
, 
=
.
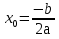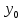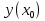Ось симметрии параболы - прямая, параллельная оси ординат и проходящая через вершину параболы.
Параболу 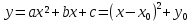можно получить сдвигом параболы
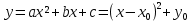вдоль координатных осей.
2. Сформулируйте для себя цель урока.
IV. Изложение нового материала.
*Теоретическое замечание (учащиеся пишут в тетрадях).
Пусть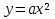 
и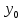 - координаты вершины параболы.
График функции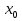 
можно построить , сдвигая параболу 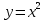вдоль оси абсцисс вправо на 
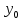или влево на 
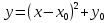и вдоль оси ординат вверх на 
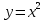или вниз на 
.
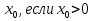Задание.
Записать аналитически функцию, график которой изображён на рисунке. (Слайд либо предварительно подготовлен плакат с осями координат и трафарет параболы, которую можно передвигать по плакату и закреплять с помощью магнита; учащимся раздаются трафарету параболы для работы в тетрадях).
Парабола получена перемещением вершины функции у=х² в точку (-2;-3)
Решение.
, 
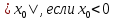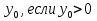
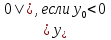
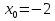
Подписываем график функции.
Теоретическое замечание.
Если ветви параболы направлены вниз, то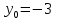 
.
Задание.
Парабола получена перемещением вершины функции у=-х² в точку (4;2)
Решение.
, 
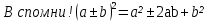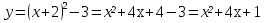
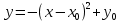
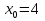
V. Закрепление нового в ходе решения .
**Задание (самостоятельно).
а) парабола получена перемещением вершины функции у=х² в точку (3;2);
б) парабола получена перемещением вершины функции у=-х² в точку (-3;-2).
Решение.
а)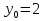
,
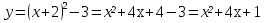
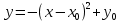
б)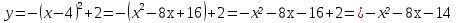
, 
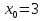
VI. Первичная проверка усвоения .
***Проверочная работа по карточкам (Приложение 1.)
1-8 карточки: парабола получена перемещением вершины функции у=х² в точку
1 вариант (2;-4)
2 вариант (-1;-4)
3 вариант (1;-4)
4 вариант (-3;-2)
5 вариант (2;-3)
6 вариант (-1;-3)
7 вариант (1;-3)
8 вариант (3;-2)
9-16 карточки: парабола получена перемещнием вершины функции у=-х² в точку
9 вариант (-3;2)
10 вариант (-1;3)
11вариант (1;3)
12вариант (-2;3)
13 вариант (3;2)
14 вариант (-1;4)
15 вариант (1;4)
16 вариант (-2;4)
Критерии оценивания.
1 карточка - «3»
2 карточки - «4»
3 карточки - «5»
№ варианта
Ответы.
1.
2.
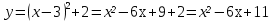
3.
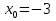
4.
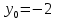
5.
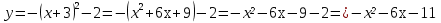
6.
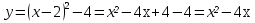
7.
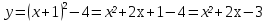
8.
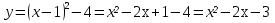
9.
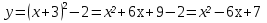
10.
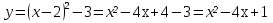
11.
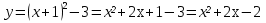
12.
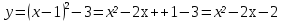
13.
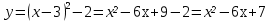
14.
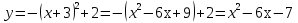
15.
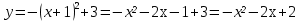
16.
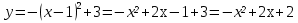
Если кто-то справился досрочно, то получает тест (Приложение 2.)
VIII. Итоги урока.
Вернёмся к цели, поставленной в начале урока. Удалось ли её достичь?
Оцените свою деятельность на уроке:
Урок был полезен, знания понадобятся в дальнейшей деятельности
Не уверен, что эти знания мне пригодятся, но я их получил
Полученные знания нужно закрепить на практике
Затрудняюсь ответить