Конспект урока по алгебре в 9 классе по теме «Арифметическая и геометрическая прогрессии»

Тема урока: « Арифметическая и геометрическая прогрессии».

Класс: 9.

Цели урока:

1. обобщить информацию по прогрессиям; совершенствовать навыки нахождения n - го члена и суммы n первых членов данных прогрессий с помощью формул; решение некоторых практических задач, в которых используются обе последовательности;

2. продолжить формирование практических навыков по теме;

3. развивать познавательный интерес учащихся, учить их видеть связь между математикой и окружающей жизнью;

4. воспитание самостоятельности, тактичного отношения друг к другу.

Задача урока: проверка усвояемости материала по теме урока.

Тип урока: повторительно - обобщающий.

Оборудование: 1) карточки - задания по теме;

2) кармашки для карточек с заданиями.

Ход урока:

1. Организационный момент

2. Постановка целей и задач урока

-- Сегодня один из последних уроков по теме « Прогрессии».

Сегодня предстоит определиться хорошо или плохо усвоен материал по данной теме. А также где и как его можно применить на практике.

-- Что для этого необходимо?

-- Для начала, вспомните, пожалуйста, определение обоих последовательностей.

( Заслушать ответы нескольких учащихся)

-- Для последующей работы необходимо повторение основных формул для работы с прогрессиями.

( Опрос 2 и более учащихся по формулам n- го члена прогрессий,

суммы n первых членов прогрессий c соответствующими записями на доске)

-- Ну а теперь в путь!

3. Практическое значение знаний и умений по теме « Прогрессии»

-- На уроках, работая с прогрессиями, мы судили о них абстрактно, как о наборе чисел объединённых некоторыми общими свойствами. На самом же деле у прогрессий достаточно длинная интересная и практичная биография.

-- Известный немецкий математик Карл Фридрих Гаусс удивлял своими знаниями особенностей чисел ещё в ранней юности. Чего только стоит история о том, как он быстро подсчитал сумму чисел от 1 до 100. Учитель ему даже не поверил в начале. А он на практике применил формулу для подсчёта суммы n -членов арифметической прогрессии.

--Ещё одна история приводится для ознакомления в вашем учебнике. Это предание об индийском принце Сираме и изобретателе шахмат учёном Сете.

Принц был восхищён остроумием игры и разнообразием возможностей шахматных фигур, что захотел отблагодарить учёного с царским размахом. Он предложил учёному выполнить любое его желание. На что Сета предложил заполнить всё шахматное поле зерном, но при обязательном условии - в каждую следующую клетку доски необходимо положить зёрен в два раза больше, чем в предыдущей.

--Выполнил ли принц пожелание учёного?

( На одной из половинок доски приводится решение этой задачи с помощью АП)

--Следующая история родом из задачника известного русского математика Магницкого.

Это история о продаже лошади. Некто продал лошадь за 156 рублей. Но покупатель через некоторое время привёл её обратно. Ему показалось, что его обманули. Тогда продавец предложил мужику купить у него гвозди на лошадиные подковы, цена которых начиналась с четверти копейки и потом увеличивалось в двое при переходе от одного гвоздя у другому. На сколько проторговался покупатель?

(Решение задачи приводится на доске в готовом виде)

--Всё это было очень давно. А сегодня где нам применить знания об АП и ГП?

--Сегодня в любом банке вам предложат вложить деньги под проценты. Подсчёт прибыли с этих вкладов и можно подсчитать с помощью АП или ГП.

--Например. У вас на руках 100 рублей. Три банка предлагают вам вложить эти деньги под простые или сложные проценты на три года. В 1-ом банке простые проценты из расчёта 3% в месяц; во 2-ом банке - простые проценты из расчёта 40% в год, а в 3-ем банке - сложные проценты из расчёта 30% в год. Какой из банков предлагает наилучший вклад?

(Решение приводится на доске по вариантам)

4. Решение задач

-- А теперь перейдём непосредственно к решению задач по теме «Арифметическая и геометрическая прогрессии». Игра «Математические тяжеловесы» вам знакома. В качестве лотов - задачи. Масса лота зависит от сложности задания. Тот, кто наберёт наибольшую массу, объявляется победителем и получает наивысший бал за урок.

--Итак! Вперёд!

(Игра может продолжаться до окончания урока)

5. Задание на дом

-- В качестве задания на дом вам предлагается подсчитать прибыль от вклада в банк за 5 лет.

6. Подведение итогов урока. Выставление оценок учащимся.

7. Физкультминутка

Физкультминутка проводится в зависимости от степени усталости учащихся на различных этапах урока.

Примеры вычислений

Задача № 1

(аn) - ГП, а1=1, q=2, n=64,

S64= .

Задача № 2

(аn) - ГП, а1=, а2=, n=24,

q=а2:а1, q=2,

S24=,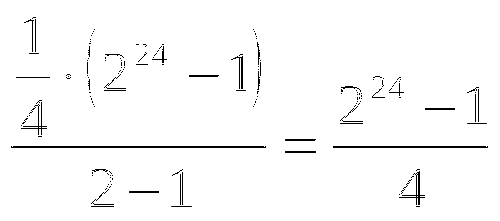

копеек > 156 рублей.

Задача № 3

А) (аn) - АП, а1=100, d=0,03·100=3, n=37,

а37=100+ 3·(37-1)=100+108=208.

Б) (аn) - АП, а1=100, d=0,4·100=40, n=4,

а4=100+40·(4-1)=100+120=220.

В) (bn) - ГП, b1=100, q=1,3, n=4,

b4=100·1,3=100·1,3=100·2,197=219,7.

Задания для игры «Математические тяжеловесы»

10 килограмм

а1=2, d=3, а4=?

а1=-5, d=2, а5=?

а1=, d=, а4=?

а1=7, d=, а5=?

а1=8, d=, а4=?

b1=2, q=-2, b5=?

b1=3, q=3, b6=?

b1=5, q=8, b5=?

b1=, q=9, b3=?

b1=, q=-4, b4=?

20 килограмм

а1=16, а8=37, d=?

а1=4, а18=-11, d=?

а1=0,5, а23=-2,3, d=?

а1=5, а8=17, d=?

а1=2, а11=-5, d=?

а1=-0,3, а7=1,9, d=?

b1=125, q=, b5=?

b1=, q=, b8=?

b7=256, q=-2, b1=?

b6=, q=, b1=?

b5=, q=, b1=?

30 килограмм

а1=14, d=0,5, аn=17,6,n=?

а1=14, d=0,5, аn=19,n=?

а1=14, d=0,5, аn=34,n=?

а1=12, d=3, аn=-6,n=?

а1=12, d=3, аn=0,n=?

а1=12, d=3, аn=9,n=?

b3=12, b5=48, q=?

b4=25, b6=16, q=?

b6=100, b8=9, q=?

b5=11, b7=99, q=?

40 килограмм

а1=4, d=2, S12=?

а1=-5, d=3, S12=?

а1=16,5, d=-1,5, S12=?

а1=5, d=3, S10=?

а1=-8, d=4, S10=?

а1=18,5, d=-2,5, S10=?

b1=3, b2=6, S6=?

b1=5, b2=-2,5, S6=?

b1=8, b2=4, S5=?

b1=-27, b2=-9, S5=?

50 килограмм

q=2, S5=93, b1=?

q=, S4=65, b1=?

q=2, S8=795, b1=?

b1=, b5=, S5=?

b2=4, b4=36, S5=?

b2=6, b4=24, S4=?

b3=, b4=, S4=?

q=, S=8, b1=?

60 килограмм

0,(17)=?

2,(4)=?

3,(16)=?

0,4(5)=?

0,6(12)=?

0,5(14)=?

0,6(3)=?

3,(1)=?