Урок по геометрии на тему Вписанный угол (7 класс)

Название методической разработки: урок геометрии

Автор методической разработки: Пушкова Роза Александровна

Учебное заведение: МБОУ «Федоровская ООШ»

Класс: 8

Количество учащихся в классе: 6

Тема: «Вписанный угол»

Цели:

1. Обучающие:

• дать определение вписанного угла; научить распознавать вписанные углы на чертежах;

• рассмотреть теорему о вписанном угле и следствия из нее; применять их при решении задач.

2. Развивающие: Обеспечить условия для:

• самостоятельного добывания знаний, осмысленного отношения к своей деятельности;

• развития логического и пространственного воображения, интуиции учащихся;

• формирования умения чётко и ясно излагать свои мысли;

• совершенствования графической культуры.

3. Воспитательные: Обеспечить условия для:

• воспитания аккуратности;

• воспитания ответственного отношения к учению;

• воспитания культуры общения;

Тип урока: урок изучения нового материала

Методы организации учебной деятельности, применяемые на уроке:

Технологии: исследовательская деятельность

Методы исследования: наблюдение, анализ, сравнение, обобщение.

Форма организации учебной деятельности, применяемая на уроке: индивидуальная, парная, групповая.

Оборудование:

Учебники, литература: Геометрия, 7-9: Учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. - М.: Просвещение, 2009.

Дидактические материалы: раздаточный материал: карточки с заданиями, листы исследования.

Этапы урока:

1. Мотивационно - целевой этап.

2. Ориентировочный этап.

3. Поисково-исследовательский этап.

4. Практический этап.

5. Рефлексивно - оценочный этап.

Ход урока

Какой угол называется центральным?

Каким соотношением связаны центральный угол и дуга, на которую он опирается?

Чем отличаются угол 4 и 5?

Как можно назвать этот угол?

Кто назовет тему урока?

Молодцы!

Откройте тетради, запишите число и тему урока «Вписанный угол».

Какую цель вы поставите перед собой на уроке?

Итак, сегодня на уроке мы изучаем вписанный угол.

Смежные, вертикальные, накрест лежащие, односторонние, соответственные, центральный

Угол с вершиной в центре окружности.

Градусная мера дуги окружности равна величине центрального угла

Вершина лежит на окружности.

Вписанный.

Вписанный угол

Записывают тему.

Высказываются.

Ориентировочный этап

Изучение любого понятия начинается с его определения. Кто сможет сформулировать определение вписанного угла?

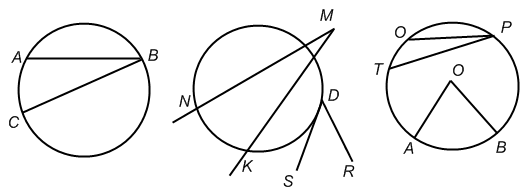
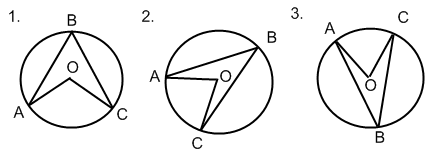
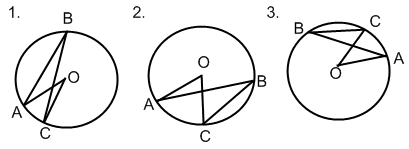
Выберите на рисунках вписанные углы:

Следующий шаг при изучении углов - его измерение. Я предлагаю вам задачу, которая лежит перед вами на столах.

К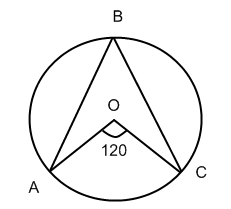ак найти вписанный угол АВС, если известна величина центрального угла?

Для того чтобы проверить ваши предположения необходимо выполнить небольшое исследование. Для исследования вам нужно следующее:

1. План; (приложение 1)

2. Таблицу для записи результатов; (приложение 2)

3. Транспортир.

Все необходимое находится у вас на столах. Исследование проводите, работая в парах, у каждой пары свой угол. На работу вам отводится 5-7 минут.

Угол, вершина которого лежит на окружности, а стороны пересекают ее.

ABC, OPT.

.

Высказывают предположения.

Поисково-исследовательский этап

Начинаем исследование.

1 группа:

2 группа:

3 группа:

План исследования:

1. Измерьте центральный угол.

2. Измерьте вписанный угол.

3. Выявите закономерность.

4. Сделайте вывод о величине вписанного угла.

Таблица результатов

Закончили исследование. Так как у вас были разные виды вписанных углов, то выслушаем представителя каждой группы. А затем обобщим ваши выводы в один общий.

Итак, какой общий вывод можно сделать?

Верным ли было наше предположение?

Давайте сравним наш вывод с учебником, откройте стр. 171, прочитайте.

Какое название носит это утверждение?

Как любая, данная теорема нуждается в доказательстве. Докажем теорему для первого случая расположения луча ВО относительно угла АВС : луч ВО совпадает с одной из сторон угла АВС.

Дано: - вписанный в окружность (О, r) опирающийся на дугу АС

Доказать:

Доказательство:

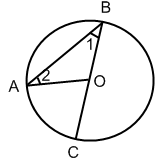< полуокружности

- равнобедренный

- внешний

или .

Что и требовалось доказать.

Доказательство 2 и 3 случая вы выполните дома.

Теперь вернемся к задаче и решим ее.

Молодцы! Итак, как измеряется вписанный угол?

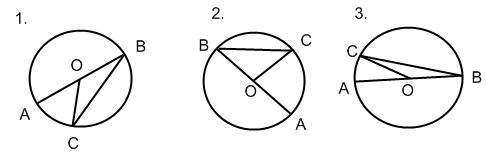
Из данной теоремы вытекают два следствия, а вот какие, вы должны сказать сами, выполнив задание в группах.

Рассмотрите рисунок, проанализируйте и сформулируйте следствие

1 группа: 2 группа:

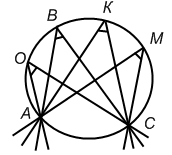
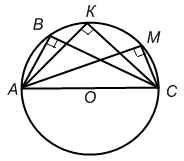
Итак, что у вас получилось?

Молодцы!

Работают в парах, результаты заносят в таблицу.

Выступления групп

Вписанный угол равен половине дуги окружности.

Верным.

Читают учебник

Теорема о вписанном угле

Вместе с учителем проводят доказательство и фиксируют его в тетради.

Решают задачу. Ответ: 60⁰

Вписанный угол измеряется половиной дуги, на которую опирается.

Выполняют задание

Выступления групп:

1 группа: вписанные углы, опирающиеся на одну и ту же дугу, равны.

2 группа: вписанный угол, опирающийся на полуокружность - прямой.

Практический этап

А где нам пригодятся знания о вписанном угле?

Итак, сейчас решим несколько задач по готовым чертежам. У вас у каждого на столах лежат задачи. Приступаем. Решаем задачи № 2, 3, 4,

Молодцы!

Для того чтобы лучше усвоить данную теорему, вы выполните дома задание:

1. Доказать теорему для 2 и 3 случаев.

2. Решить 2 задачи на выбор.

Для решения задач.

Один ученик решает задачу с обратной стороны доски, остальные в тетрадях, затем проверяют.

Рефлексивно - оценочный этап

Итак, настало время подвести итоги.

С каким новым понятие мы познакомились?

Какой угол называется вписанным?

Как измеряется вписанный угол?

Какие два следствия вытекают из теоремы о вписанном угле?

Достигли ли вы цели, которую ставили перед собой на уроке?

У вас на столах лежат листочки с незаконченными предложениями:

• сегодня я узнал…

• было интересно…

• было трудно…

• я выполнял задания…

• я понял, что…

• теперь я могу…

• я почувствовал, что…

• я приобрел…

• я научился…

• у меня получилось …

• я смог…

• я попробую…

• меня удивило…

• урок дал мне для жизни…

• мне захотелось…

выберите одно из предложенных предложений и закончите его.

Спасибо! А теперь настала моя очередь:

Я хочу поблагодарить вас за хорошую работу на уроке, вы молодцы, и если вы будете с тем же упорством добывать знания, вы станете успешными людьми.

Еще раз спасибо. Урок окончен.

Вписанный угол

Угол, вершина которого лежит на окружности, а стороны пересекают ее.

Вписанный угол измеряется половиной дуги, на которую опирается.

1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

2. Вписанный угол, опирающийся на полуокружность - прямой.

Высказываются.

Выбирают предложение и заканчивают его.