- Учителю
- Задачи оптимизации
Задачи оптимизации
Геометрия в задачах оптимизации
Содержание
1. Введение……………………………………………………………………с.2
2. Задание выпуклых многоугольников с помощью неравенств……..с.3
3. Задачи оптимизации на плоскости……………………………………с.4-6
4. Задание выпуклых многогранников с помощью неравенств……с.7
5. Задача оптимизации в пространстве………………………………..с.8-9
6. Заключение ………………………………………………………………...с.9
7. Список используемой литературы и Интернет-ресурсов……………c.10
Введение
Среди прикладных задач, решаемых с помощью математики, выделяются так называемые задачи оптимизации. Среди них:
- транспортная задача о составлении оптимального способа перевозок грузов;
- задача о диете, то есть о составлении наиболее экономного рациона питания, удовлетворяющего определенным медицинским требованиям;
- задача о наилучшем использовании ресурсов;
- задача о смесях, то есть о получении продукции с заданными свойствами при наименьших затратах;
- задача составления оптимального плана производства;
- задача рационального использования посевных площадей и т.д.
Несмотря на различные содержательные ситуации в этих задачах, математические модели, их описывающие, имеют много общего, и все они решаются одним и тем же методом, разработанным отечественным математиком Л. В. Канторовичем (1912 - 1986). Несколько слов о разработчике метода.
Леонид Витальевич Канторович (6 (19) января 1912, Санкт-Петербург - 7 апреля 1986, Москва) - советский математик и экономист, лауреат Нобелевской премии по экономике 1975 года «За вклад в теорию оптимального распределения ресурсов». Пионер и один из создателей линейного программирования.

Леонид Витальевич впервые применил функциональный анализ к вычислительной математике, развил общую теорию приближённых методов, построил эффективные методы решения операторных уравнений. Также развил идею оптимальности в экономике. Установил взаимозависимость оптимальных цен и оптимальных производственных и управленческих решений.
Л. В. Канторович - представитель петербургской математической школы П. Л. Чебышева, ученик Г. М. Фихтенгольца и В. И. Смирнова. Канторович разделял и развивал взгляды П. Л. Чебышева на математику как на единую дисциплину, все разделы которой взаимосвязаны, взаимозависимы и играют особую роль в развитии науки, техники, технологии и производства. Л. В. Канторович выдвигал тезис взаимопроникновения математики и экономики и стремился к синтезу гуманитарных и точных технологий знания. Творчество Канторовича стало образцом научного служения, базирующегося на универсализации математического мышления.
Задание выпуклых многоугольников с помощью неравенств
Пусть прямая задана уравнением 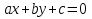 и проходит через точку
и проходит через точку 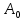 (
(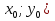 . Ее вектор нормали
. Ее вектор нормали 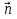 имеет координаты
имеет координаты 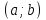 и определяет полуплоскость. Точка A(x; y) принадлежит этой полуплоскости в случае, если угол между векторами
и определяет полуплоскость. Точка A(x; y) принадлежит этой полуплоскости в случае, если угол между векторами 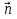 и
и 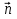 не превосходит 90˚, т.е. в том случае, если скалярное произведение этих векторов больше или равно нулю, т.е.
не превосходит 90˚, т.е. в том случае, если скалярное произведение этих векторов больше или равно нулю, т.е. 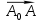 = a(x
= a(x 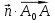
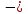 ) + b(y
) + b(y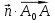
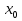 )
) 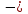 0. При этом
0. При этом 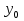 Следовательно, точка A(x; y) принадлежит этой полуплоскости, если выполняется неравенство ax + by +c
Следовательно, точка A(x; y) принадлежит этой полуплоскости, если выполняется неравенство ax + by +c 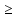
Аналогично точка A(x; y) принадлежит другой полуплоскости по отношению к данной прямой, если выполняется неравенство ax + by +c 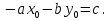 .
.
Для того, чтобы определить, какой из двух полуплоскостей принадлежит точка A (x; y), достаточно подставить ее координаты в левую часть уравнения прямой и найти знак получившегося значения.
Покажем, как с помощью неравенств можно задавать выпуклые многоугольники.
Действительно, пусть стороны выпуклого многоугольника лежат на прямых, задаваемых уравнениями:
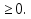
……………………,
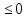
Тогда сам многоугольник является пересечением соответствующих полуплоскостей, и, следовательно, для его точек должна выполняться система неравенств вида
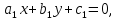
которая и определяет этот многоугольник.
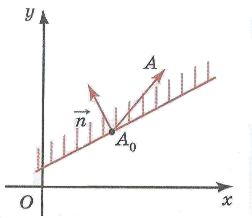
Например, неравенства 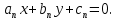 которые можно переписать в виде системы
которые можно переписать в виде системы
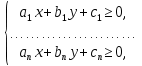
определяют единичный квадрат.
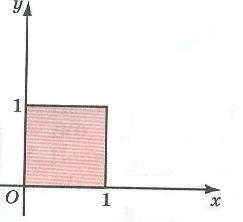
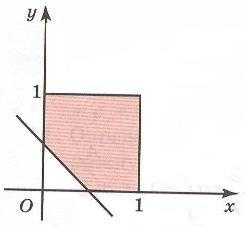
Если к этим неравенствам добавить еще одно неравенство
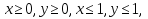
то соответствующий многоугольник получается из квадрата отсечением треугольника.
Задачи оптимизации на плоскости
В качестве примера задач оптимизации рассмотрим следующие задачи.
Задача 1. На трех складах хранится сырье одинакового вида в количестве соответственно 10 т, 20 т, 30 т. На завод нужно завести 35 т сырья. Найдите наиболее выгодный вариант перевозок, если расстояния от складов равны соответственно 7 км, 5 км, 8 км.
Р е ш е н и е. Составим математическую модель. Для этого обозначим через х и у количество тонн сырья, которое нужно перевезти соответственно с первого и второго складов на завод. Тогда с третьего склада нужно будет перевезти 35 - (x + y) тонн сырья. Занесем данные в таблицу, где 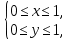 склады.
склады.
Склад
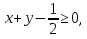
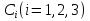
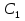
Количество сырья (т)
10
20
30
Расстояние до завода (км)
7
5
8
Количество сырья, перевезенное на завод (т)
x
y
35 - (x + y)
Все величины, входящие в эту таблицу, должны быть неотрицательны. Поэтому имеем систему неравенств:
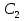
Систему можно переписать иначе:
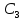
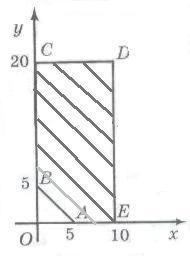
Эта система определяет многоугольник ABCDE. Найдем на нем наименьшее значение функции
F = 7x + 5y + 8(35 - x - y), или F = - x - 3y + 280.
Найдем координаты вершин многоугольника: А(5;0), В(0;5), С(0;20), D(10;20) , E(10;0). Тогда
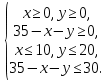
Таким образом, наименьшее значение функция принимает в точке D(10;20). Следовательно, наиболее выгодно с первого склада перевезти на завод 10 т сырья, со второго - 20 т и с третьего - 5 т.
Задача 2. Установка собирается из трех различных деталей - А, Б, В. На одном станке можно за смену изготовить либо 12 деталей типа А, 18 - Б, 30 -В. (первый режим), либо 20 деталей типа А, 15 - Б, 9 - В (второй режим). Хватит ли 100 станков, чтобы изготовить за смену детали для 720 установок? Какое наименьшее количество станков (и с какими режимами работы) нужно для выполнения заказа?
Режим
Кол-во станков
детали
А
Б
В
I
x
12
18
30
II
y
20
15
9
Р е ш е н и е. Пусть х, у - количество станков, работающих в первом и втором режимах соответственно. Для изготовления 720 деталей нужно, чтобы выполнялись неравенства
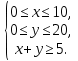
Кроме того, поскольку количество деталей должно быть неотрицательно, нужно, чтобы выполнялись неравенства 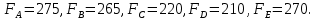 Перепишем все эти неравенства в виде системы:
Перепишем все эти неравенства в виде системы:
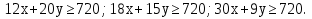
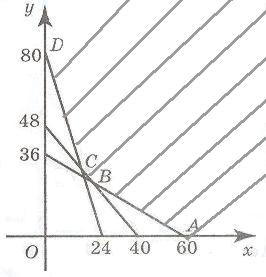
Эта система неравенств определяет фигуру на плоскости.
Вершины A и D имеют координаты (60;0) и (0;80) соответственно. Для нахождения координат вершин B и C нужно решить системы уравнений
В: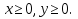 C:
C: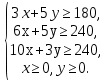
В результате имеем В(20;24), С(15;30).
Для нахождения наименьшего значения функции F = x + y, вычислим ее значения в вершинах: 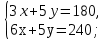 Наименьшее значение принимается в вершине В, и оно равно 44.
Наименьшее значение принимается в вершине В, и оно равно 44.
Таким образом, для выпуска 720 деталей достаточно 44 станка, из которых 20 работает в первом режиме, а 24 - во втором.
Задача 3. Для изготовления двух видов продукции используют три вида сырья: 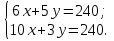 Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а так же величина прибыли, получаемая от реализации единицы продукции, приведены в таблице.
Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а так же величина прибыли, получаемая от реализации единицы продукции, приведены в таблице.
Вид сырья
Запас сырья
Количество единиц сырья, идущих на изготовление единицы продукции
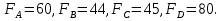
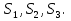
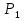
20
2
5
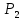
40
8
5
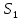
30
5
6
Прибыль от единицы продукции, руб.
50
40
Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.
Р е ш е н и е. Обозначим через x количество единиц продукции 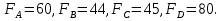 , а через y - количество единиц продукции
, а через y - количество единиц продукции 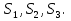 . Тогда количество единиц сырья, расходуемое на изготовление продукции, а так же запасы сырья, получим систему ограничений:
. Тогда количество единиц сырья, расходуемое на изготовление продукции, а так же запасы сырья, получим систему ограничений:
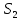
которая показывает, что количество сырья, расходуемое на изготовление продукции, не может превысить имеющихся запасов. Если продукция 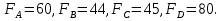 не выпускается, то
не выпускается, то 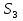 То же самое получаем и для второго вида продукции. Таким образом, на наши неизвестные должно быть наложено ограничение неотрицательности.
То же самое получаем и для второго вида продукции. Таким образом, на наши неизвестные должно быть наложено ограничение неотрицательности.
Конечную цель решаемой задачи - получение максимальной прибыли - выразим как функцию переменных x и y. Реализация единиц продукции даст 50x и 40y руб. прибыли, суммарная прибыль Z = 50x + 40 y (руб.).
Неделимость продукции в условии не оговорена, поэтому переменные
могут быть и дробными числами.
Требуется найти такие х и y, при которых функция Z достигнет максимума, т.е. найти максимальное значение линейной функции
Z = 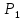 при ограничениях:
при ограничениях:
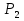
Построим многоугольник решений. Для этого в системе координат 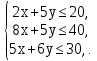 изобразим граничные прямые
изобразим граничные прямые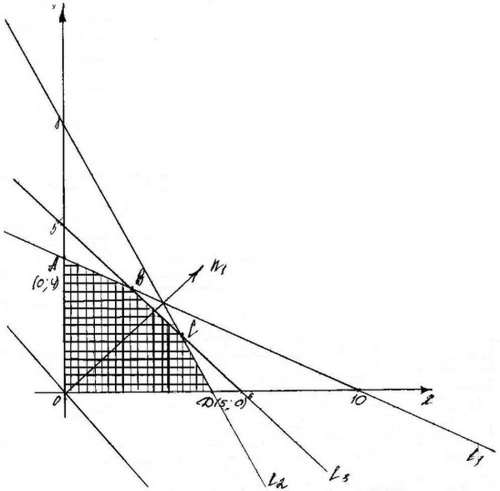
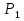
Взяв какую-нибудь точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Многоугольником решений данной задачи является ограниченный пятиугольник OABCD.
Для построения прямой 50x + 40 y = 0 строим радиус-вектор 
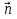 и через точку О проводим прямую, перпендикулярную ему. Построенную прямую Z = 0 перемещаем параллельно самой себе в направлении вектора
и через точку О проводим прямую, перпендикулярную ему. Построенную прямую Z = 0 перемещаем параллельно самой себе в направлении вектора 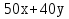 . Из рисунка следует, что опорной по отношению к многоугольнику решений эта прямая становится в точке С, где функция Z принимает максимальное значение. Точка С лежит на пересечении прямых
. Из рисунка следует, что опорной по отношению к многоугольнику решений эта прямая становится в точке С, где функция Z принимает максимальное значение. Точка С лежит на пересечении прямых 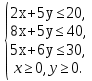 и
и 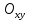 . Для определения ее координат решим систему уравнений
. Для определения ее координат решим систему уравнений
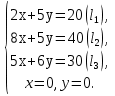
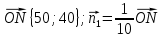
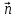
Оптимальный план задачи: 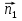 = 3,9;
= 3,9; 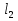 Подставляя значения в линейную функцию, получаем, что максимальная прибыль равна 260,3 руб., и чтобы ее заработать надо запланировать производство 3,9 ед. продукции
Подставляя значения в линейную функцию, получаем, что максимальная прибыль равна 260,3 руб., и чтобы ее заработать надо запланировать производство 3,9 ед. продукции 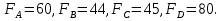 и 1,7 ед. продукции
и 1,7 ед. продукции 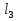
Задание выпуклых многогранников с помощью неравенств
Плоскость в пространстве задается уравнением 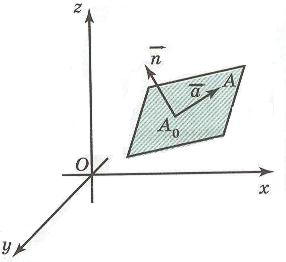
ax + by + cz + d = 0, (*),
где a, b, c, d - действительные числа, причем a,b,c не равны нулю и составляют координаты вектора 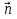 , перпендикулярного этой плоскости и называемого вектором нормали.
, перпендикулярного этой плоскости и называемого вектором нормали.
4 частных случая расположения плоскости:
-
ax + by + cz = 0 (d = 0) - плоскость проходит через начало координат;
-
ax + by + d = 0 (с = 0) - параллельно
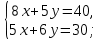 ;
; -
ax + by = 0 (с = d = 0) - пересекает
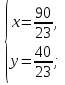 ;
; -
ax + d = 0 (b = с = 0) -
 .
.
A(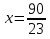 точки пересечения плоскости с осью абсцисс, осью ординат и осью аппликат соответственно. Если уравнение плоскости разделить на d, то получим уравнение плоскости в отрезках
точки пересечения плоскости с осью абсцисс, осью ординат и осью аппликат соответственно. Если уравнение плоскости разделить на d, то получим уравнение плоскости в отрезках
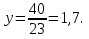 .
.
Заметим, что если плоскость задана уравнением (*), то неравенства
ax + by + cz + d  ax + by + cz + d
ax + by + cz + d 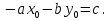 определяют полупространства, на которые эта плоскость разбивает пространство. Для того, чтобы определить, какому из двух полупространств принадлежит точка А (x; y. z), достаточно подставит ее координаты в левую часть уравнения плоскости и найти знак получившегося значения.
определяют полупространства, на которые эта плоскость разбивает пространство. Для того, чтобы определить, какому из двух полупространств принадлежит точка А (x; y. z), достаточно подставит ее координаты в левую часть уравнения плоскости и найти знак получившегося значения.
Поменяв знаки чисел a, b, c, d, второе неравенство всегда можно свести к первому.
Покажем, как с помощью таких неравенств в пространстве можно задавать выпуклые многогранники.
Например, неравенства 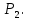 которые можно переписать в виде системы
которые можно переписать в виде системы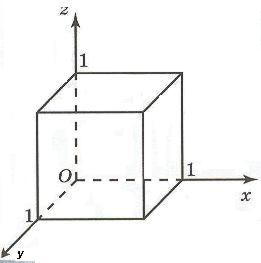
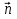
определяют единичный куб в пространстве.
Если к этим неравенствам добавить еще одно неравенство
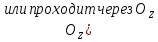
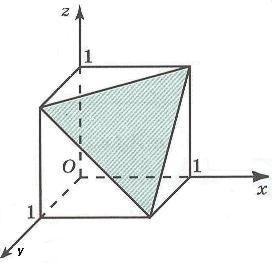
то соответствующий многогранник получается из куба отсечением пирамиды.
Задача оптимизации в пространстве
Задача. Пусть на четыре завода 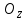 ,
, 
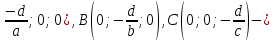
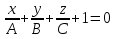 требуется завезти сырье одинакового вида, которое хранится на двух складах
требуется завезти сырье одинакового вида, которое хранится на двух складах 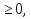 ,
, 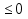 . Потребность данных заводов в сырье каждого вида указана в таблице , а расстояние от склада до завода - в таблице 2. Требуется найти наиболее выгодный вариант перевозок.
. Потребность данных заводов в сырье каждого вида указана в таблице , а расстояние от склада до завода - в таблице 2. Требуется найти наиболее выгодный вариант перевозок.
Таблица 1
Наличие сырья на складе (т)
Потребность завода в сырье (т)
С1
С2
З1
З2
З3
З4
20
25
8
10
12
15
Таблица 2
Склад
Расстояние от склада до завода (км)
З1
З2
З3
З4
С1
5
6
4
10
С2
3
7
3
7
Для решения этой задачи в первую очередь проанализируем ее условие и переведем его на язык математики, то есть составим математическую модель. Для этого количество сырья, которое нужно перевезти со склада С1 на заводы З1, З2, З3, обозначим через x, y, z. Тогда на четвертый завод с этого склада нужно перевезти 20 - x - y - z сырья в тоннах, а со второго нужно перевезти 8 - x, 10 - y, 12 - z, x + y + z - 5 сырья в тоннах. Запишем эти данные в таблицу 3.
Таблица 3
Склад
Количество сырья, перевезенное на завод (т)
З1
З2
З3
З4
С1
x
y
z
20 - x - y - z
С2
8 - x
10 - y
12 - z
x + y + z - 5
Поскольку все величины, входящие в эту таблицу, должны быть неотрицательными, получим следующую систему неравенств:
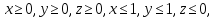
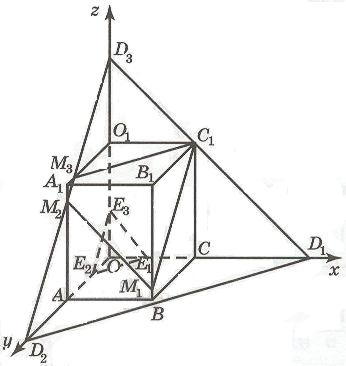
Эта система неравенств определяет некоторый многогранник. Для того чтобы его построить, изобразим сначала многогранник, определяемый первой и второй строкой данной системы. На рисунке это параллелепипед OABCO1A1B1C1. Уравнение 20 - x - y - z = 0 определяет плоскость D1D2D3, которая, пересекает параллелепипед, образуя многоугольник M1M2M3C1. Уравнение
x + y + z - 5 = 0 определяет плоскость, которая пересекает параллелепипед и образует в нем треугольник E1E2E3. На многограннике M1M2M3C1CBAE1E2E3O1, где M1(8,10,2), M2(0,10,10), M3(0,8,12), C1(8,0,12), C(8,0,0), B(8,10,0), A(0,10,0), E1(5,0,0), E2(0,5,0), E3(0,0,5), O1(0,0,12), выполняются все условия данной системы. Назовем его многогранником ограничений.
Для нахождения общего числа тонно-километров умножим расстояния от складов до заводов на перевозимое количество сырья и полученные результаты сложим. Общее число тонно-километров выражается формулой:
5x + 6y + 4z + 10(20 - x - y - z) + 3(8 - x) + 7(10 - y) +
+ 3(12 - z) + 7(x + y + z - 5) = 295 - x - 4y - 2z.
Таким образом, задача сводится к отысканию наименьшего значения функции F = 295 - x - 4y - 2z на многограннике ограничений. Для этого достаточно найти наибольшее значение функции f = x + 4y + 2z. Тогда Fmin = 295 - fmax.
Вычислим значение функции f = x + 4y + 2z в вершинах многогранника ограничений: f(M1) = 52, f(M2) = 60, f(M3) = 56,f(C1) = 32, f(C) = 8, f(B) = 48, f(A) = 40, f(E1) = 5, f(E2) = 20, f(E3) = 10, f(O1) = 24.
Легко видеть, что максимальное значение функции f равно 60. Тогда Fmin = 295 - 60 = 235. Это значение функция F принимает в точкеM2(0,10,10). Таким образом, наиболее выгодный вариант перевозок задается таблицей 4.
Таблица 4
Склад
Количество сырья (в т), перевезенное на заводы
З1
З2
З3
З4
С1
0
10
10
0
С2
8
0
2
15
Заключение
Закончив работу над темой «Геометрия в задачах оптимизации», мы сделали следующие выводы:
- основополагающим свойством в задачах оптимизации является следующий факт: наибольшее и наименьшее значения линейная функция достигает в вершинах многоугольников или многогранников ограничений;
- если число переменных равно 2-м, то в процессе решения задачи получится многоугольник, а если число переменных равно 3-м - многогранник;
- в реальных задачах число независимых переменных значительно больше трех, и для получения геометрической интерпретации этих задач требуется рассмотрение n-мерного пространства и n-мерных многогранников с очень большим n. При решении таких задач используются ЭВМ.
Таким образом, хотя пространственные свойства окружающего нас мира хорошо описываются геометрическим трехмерным пространством, потребности практической деятельности человека приводят к необходимости рассмотрения пространств большей размерности, которые изучаются в специальном разделе математики - многомерной геометрии.
Список используемой литературы и Интернет-ресурсов
-
Ефимов Н.В. Краткий курс аналитической геометрии. Москва: Издательство «Наука», 1975 год
-
Смирнова И.М., Смирнов В.А. Геометрия 7-9 классы. Москва: Издательство «Мнемозина», 2009 год
-
Смирнова И.М., Смирнов В.А. Геометрия 10-11 классы. Москва: Издательство «Мнемозина», 2009 год
-
Волков В.А. Элементы линейного программирования. Москва: Издательство «Просвещение», 1975 год
-
Беляева Е.С., Монахов В.М. Экстремальные задачи. Москва: Издательство «Просвещение», 1977 год
-
www.wikipedia.ru
12