- Учителю
- Урок математики в 11 классе по теме «Некоторые способы решения иррациональных уравнений»
Урок математики в 11 классе по теме «Некоторые способы решения иррациональных уравнений»

Ведущей линией учебника А.Г.Мордковича (издательство «Мнемозина») является функционально-графическая линия. Иррациональные уравнения изучаются в 8 классе на очень примитивном уровне.
При этом иррациональные уравнения изучаются до введения иррациональных чисел, что, по-моему мнению, не совсем удобно.
В учебнике и задачнике для 10 - 11 классов содержится глава, посвященная методам решения уравнений. Отдельной темы, содержащей изучение только иррациональные уравнения нет.
А решение иррациональных уравнений зачастую вызывает затруднения, так как требуют хорошего знания теоретического материала, умения проводить исследования различных ситуаций.
У многих учеников единственным устойчивым знанием является применение метода возведения обеих частей уравнения в одну и ту же степень. Для некоторых этот метод является единственным.
При этом иногда ученики забывают делать проверку найденных корней после возведения частей уравнения в чётную степень корня.
Все высвеченные проблемы подвели меня к мысли, что необходимо уделить больше внимания вопросу изучения иррациональных уравнений и рассмотреть более глубоко этот материал на уроках математики.
Урок в 11 классе по теме:
«Некоторые способы решения иррациональных уравнений»
Цитата урока: (выписана на доске)
«Знание только тогда - знание, когда оно добыто усилием собственной мысли, а не памятью» - слова Л.Н. Толстого.
Цель:
-
обобщение знаний учеников по данной теме;
-
демонстрация различных методов решения иррациональных уравнений;
-
показ возможности решения иррациональных уравнений на основе исследования;
-
формирование навыка самообразования, самоорганизации, умения анализировать, сравнивать, обобщать, делать выводы;
-
воспитание самостоятельности, умения выслушивать других и умения общаться в группе;
-
повышение интереса к предмету.
Форма проведения: семинарское занятие.
Оборудование: компьютер, мультимедийный проектор.
Ход занятия:
Учитель:
Сегодня мы поговорим об иррациональных уравнениях.
На доске приведены примеры уравнений иррациональных и не являющихся иррациональными.
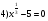
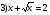
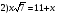 1)
1) ![]()
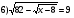
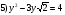
Назовите те уравнения, которые являются иррациональными.
Дайте определения иррационального уравнения.
Ответы учеников.(иррациональными являются уравнения 1), 3), 4), 6). Определение иррационального уравнения:
Иррациональным называют уравнение, в котором переменная содержится под знаком радикала или под знаком возведения в дробную степень.)
I. Учитель:
На предыдущих уроках мы рассматривали решение иррациональных уравнений методом возведения обеих частей уравнения в степень корня (в основном в квадрат). При возведении частей уравнения в чётную степень мы получаем уравнение-следствие, решение которого приводит иногда к появлению посторонних корней. И тогда обязательной частью решения уравнения является проверка корней или нахождение области определения уравнения.
Однако при решении иррациональных уравнений не всегда следует сразу приступать к «слепому» применению известного алгоритма решения.
В заданиях Единого государственного экзамена имеется довольно много уравнений, при решении которых необходимо выбрать такой способ решения, который позволяет решить уравнения проще, быстрее. Поэтому необходимо знать и другие методы решения иррациональных уравнений, с некоторыми из них мы сегодня познакомимся.
При подготовке к уроку некоторые ученики получили листы-рекомендации, в которых рассматриваются основные приёмы решения иррациональных уравнений. Ребята ознакомились с предложенными решениями и подобрали свои уравнения, решить которые предстоит нам на уроке.
II.Выступление учеников
1 ученик.
Решение иррационального уравнения методом возведения обеих частей уравнения в степень корня.
х + 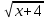 = 3х - 7
= 3х - 7
Решим данное уравнение традиционным способом - методом возведения обеих частей в квадрат. Слагаемое, содержащее квадратный корень оставим в левой части уравнения, а х перенесём в правую часть.
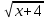 = 2х - 7
= 2х - 7
Возведём обе части уравнения в квадрат:
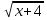 =
= 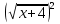
Получаем:
х + 4 = 4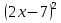 - 28х + 49
- 28х + 49
Перенесём все члены уравнения в одну часть, получаем квадратное уравнение
4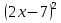 - 29х + 45 = 0
- 29х + 45 = 0
Корни этого уравнения х = 5 и х = 2,25
Решая это уравнение мы возводили обе части уравнения в квадрат. При возведении обеих частей уравнения в любую четную степень получается уравнение, являющееся не равносильное данному, а являющееся следствием исходного, следовательно, при этом возможно появление посторонних корней. Поэтому необходимым условием решения является проверка корней.
Если х = 5, то 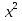 = 10 - 7
= 10 - 7
3 = 3 - верно
х = 5 - корень уравнения
Если х = 2,25, то 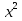 = 4,5 - 7
= 4,5 - 7
2,5 = - 2,5 - неверно
х = 2,25 посторонний корень
Ответ: х = 5
Предлагаю решить в классе уравнение: ![]()
2 ученик. Решение уравнения методом исследования области определения уравнения.
Пусть дано уравнение: 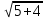 -
- 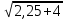 =
= 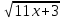 -
- 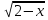
Возведение обеих частей в квадрат приведёт нас к громоздким вычислениям и трате времени на экзамене.
Воспользуемся методом исследования области допустимых значений заданного уравнения.
Область допустимых значений данного уравнения определяется системой неравенств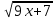 <=>
<=> 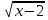 <=> х=2
<=> х=2
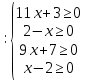
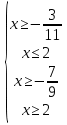
2
х
Данное уравнение определено только при х = 2.
Проверим, является ли число 2 корнем уравнения:
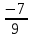 -
- 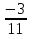 =
= 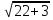 -
- 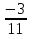
5 = 5 - верно.
Ответ: х = 2.
Попробуйте решить уравнение: 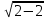 = х - 2
= х - 2
3 ученик. Использование свойства монотонности функции.
Я хочу рассказать об уравнениях, решение которых основывается на свойстве монотонности функций. Существуют теоремы:
Теорема 1. Пусть уравнение имеет вид: f(x) = с, где f(x) -монотонно возрастающая (убывающая) функция, а с - число, входящее область значений функции f(x), тогда уравнение f(x) = с имеет единственный корень.
Теорема 2. Пусть уравнение имеет вид f(x)= g(x), где функции f(x) и g(x) «встречно монотонны», т.е. f(x) возрастает, а g(x) убывает или наоборот, то такое уравнение имеет не более одного корня.
Если удается заметить эти свойства функций в уравнении или привести уравнение к таким видам, и при этом нетрудно угадать корень уравнения, то он и будет единственным решением данного уравнения.
Пример для изучения
Пусть дано уравнение: 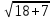 +
+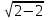 = 6
= 6
ОДЗ уравнения: х+6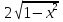 0; х
0; х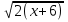
Функции 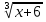 =
= 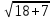 и
и 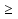 =
= 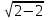 являются возрастающими на промежутке [- 6;
являются возрастающими на промежутке [- 6; 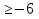 , поэтому функция у =
, поэтому функция у = 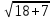 +
+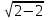 так же является возрастающей на этом промежутке, и следовательно принимает любое значение, в том числе и 6, только один раз. Значит, уравнение имеет единственный корень.
так же является возрастающей на этом промежутке, и следовательно принимает любое значение, в том числе и 6, только один раз. Значит, уравнение имеет единственный корень.
Найдём этот корень подбором.
х = 2.
Проверкой убеждаемся, что число 2 является корнем данного уравнения.
Ответ: х = 2.
Я предлагаю решить на уроке уравнение:
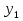 +
+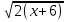 = 9 -
= 9 - 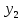
Это уравнение можно попытаться решить возведением обеих частей в квадрат (трижды!). Однако при этом получится уравнение четвертой степени.
Попробуйте использовать свойства монотонности функций, входящих в уравнение.
Ответ: х = 1
4 ученик Метод введения новой перменной.
Удобным средством решения иррациональных уравнений иногда является метод введения новой переменной, или «метод замены». Метод обычно применяется в случае, если в уравнении неоднократно встречается некоторое выражение, зависящее от неизвестной величины. Тогда имеет смысл обозначить это выражение какой-нибудь новой буквой и попытаться решить уравнение сначала относительно введенной неизвестной, а потом уже найти исходную неизвестную.
Пример для изучения:
Дано уравнение: 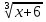 +
+ 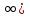 =
= 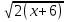
ОДЗ уравнения: х 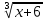 х
х 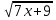
Пусть 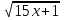 , тогда
, тогда 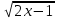
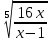
Получаем уравнение t + 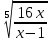 =
= 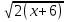
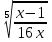
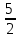
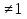 =
= 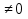
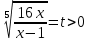 = 2
= 2
Тогда
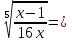 или
или 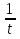
Возведём обе части уравнения в 5-ю степень. При возведении обеих частей уравнения в нечётную степень получаем уравнение, равносильное данному, следовательно, не требуется проверка найденных корней. Получаем
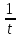 ; х =
; х = 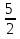
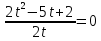 ; х = 2
; х = 2
Ответ: х = 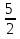 ; х = 2
; х = 2
В классе я предлагаю решить уравнение: ![]()
5 ученик Метод оценки частей уравнения.
Рассмотрим уравнение: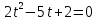 +
+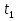 = 14х -
= 14х - 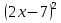
Запишем уравнение в виде 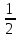 +
+ 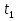 = -(
= -(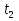 +49)
+49)
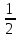 +
+ 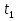 = -
= - 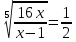
Так как левая часть данного уравнения неотрицательная, а
правая - неположительная при любых допустимых значениях x ,
то равенство возможно только в том случае, когда они обе части уравнения
равны нулю. Легко убедиться, что это возможно только при х = 7.
Для решения в классе предлагаю уравнение: 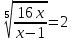
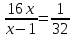 +
+ 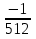 = 0
= 0
III. Работа учеников в группах.
После прослушивания выступающих начинается работа учеников в группах по решению предложенных уравнений.
Учитель контролирует работу групп, даёт консультации.
IV . Домашнее задание № 1712 - 1719 (а) стр 253 задачника
V/ Итог урока:
рефлексия
Вопросы рефлексии:
Как вы считаете, насколько полезным было проведенное занятие?
Получены ли новые знания и умения?
Кратко опишите, какие моменты занятия вам особенно запомнились.
Каких моментов занятия вам хотелось бы избежать?
Какие трудности вы испытали при изучении материала, при ответе на вопросы, в ходе решения заданий? Сумели ли вы их преодолеть? Если да, то как?
Опишите свои впечатления от проведенного занятия. Хотели бы вы в будущем принимать участие в таких занятиях?